 |
Геометрические и физические приложения
|
|
|
|
1) Длина кривой.
Если подынтегральная функция f(x, y, z) ≡ 1, то из определения криволинейного интеграла 1-го рода получаем, что в этом случае он равен длине кривой, по которой ведется интегрирование:
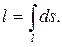(39)
2) Масса кривой.
Считая, что подынтегральная функция γ (x, y, z) определяет плотность каждой точки кривой, найдем массу кривой по формуле
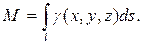(40)
Пример 6.
Найти массу кривой с линейной плотностью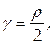 
заданной в полярных координатах уравнением ρ =4 φ, где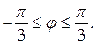 
Решение.
Используем формулу (40) с учетом того, что кривая задана в полярных координатах:
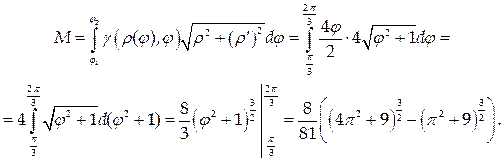
3) Моменты кривой l:
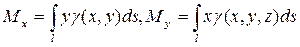- (41)
- статические моменты плоской кривой l относительно осей О х и О у;
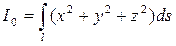- (42)
- момент инерции пространственной кривой относительно начала координат;
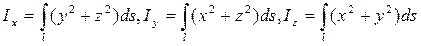- (43)
- моменты инерции кривой относительно координатных осей.
-
4) Координаты центра масс кривой вычисляются по формулам
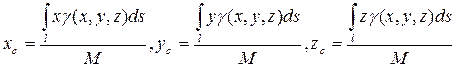. (44)
5) Работа силы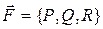 
, действующей на точку, движущуюся по кривой (АВ):
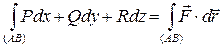, (45)
Пример 7.
Вычислить работу векторного поля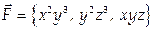 
вдоль отрезка прямой от точки А (-2;-3;1) до точки В (1;4;2).
Решение.
Найдем канонические и параметрические уравнения прямой АВ:
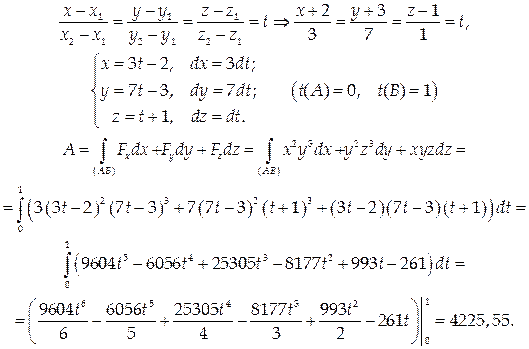
6) Площадь криволинейной поверхности, уравнение которой
z = f(x, y), можно найти в виде:
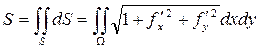(46)
(Ω – проекция S на плоскость О ху).
7) Масса поверхности
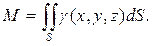(47)
Пример 8.
Найти массу поверхности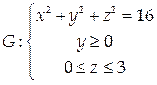 
с поверхностной плотностью γ = 2 z 2 + 3.
Решение.
На рассматриваемой поверхности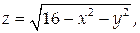 
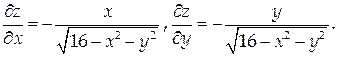Тогда
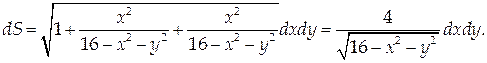
Проекцией D этой поверхности на координатную плоскость Оху является полукольцо с границами в виде дуг концентрических окружностей радиусов 3 и 4.
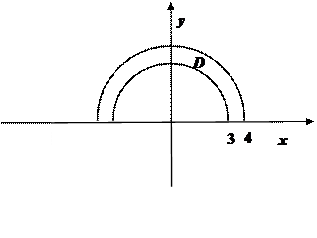
Применяя формулу (47) и переходя к полярным координатам, получим:
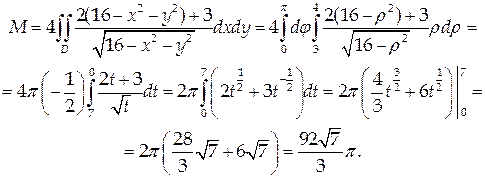
8) Моменты поверхности:
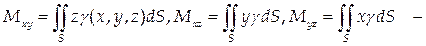(48) статические моменты поверхности относительно координатных плоскостей O xy, O xz, O yz;
|
|
|
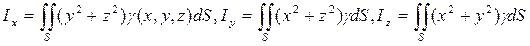
(49)
- моменты инерции поверхности относительно координатных осей;
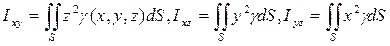- (50)
- моменты инерции поверхности относительно координатных плоскостей;
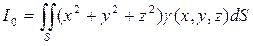- (51)
- момент инерции поверхности относительно начала координат.
9) Координаты центра масс поверхности:
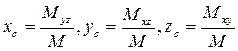. (52)
III. Теория поля
Если в каждой точке М определенной пространственной области задано значение некоторой скалярной или векторной величины, то говорят, что задано поле этой величины (соответственно скалярное или векторное).
Если в некоторой области задано скалярное поле U(x,y,z), то вектор
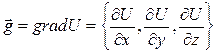(53)
называется градиентом величины U в соответствующей точке.
Пусть дано векторное поле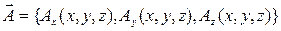 
. Интеграл
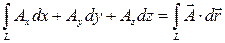(54)
называется линейным интегралом от вектора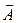 
вдоль кривой L. Если кривая L замкнута, то этот интеграл называют циркуляцией вектора 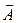вдоль кривой L.
Пример 9.
Вычислить циркуляцию векторного поля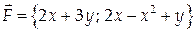 
по контуру Г, состоящему из частей линий 
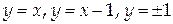(направление обхода положительно).
Решение.
Воспользуемся формулой Грина:
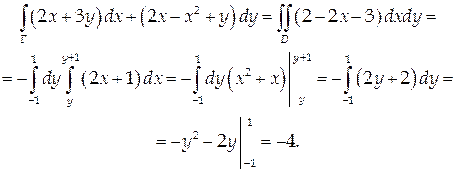
Ротором или вектором вихря векторного поля A = { Ax, Ay, Az }, где Ax, Ay, Az – функции от x, y, z, называется вектор, определяемый следующим образом:
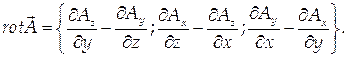(55)
Рассмотрим векторное поле А (М), определенное в пространственной области G, ориентированную гладкую поверхность S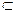 
G и поле единичных нормалей п (М) на выбранной стороне поверхности S.
Поверхностный интеграл 1-го рода
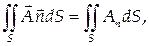(56)
где An – скалярное произведение соответствующих векторов, а Ап – проекция вектора А на направление нормали, называется потоком векторного поля А(М) через выбранную сторону поверхности S.
Пример 10.
Найти поток векторного поля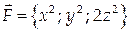 
через часть плоскости 
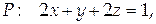ограниченную координатными плоскостями (нормаль к плоскости образует острый угол с осью Oz).
Решение.
Проекцией данной поверхности на координатную плоскость Оху является треугольник с вершинами в точках А (0;0), В (0;1), С (½; 0). Найдем координаты единичной нормали к плоскости:
|
|
|
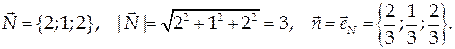
Вычислим соответствующий поверхностный интеграл (формула (56)):
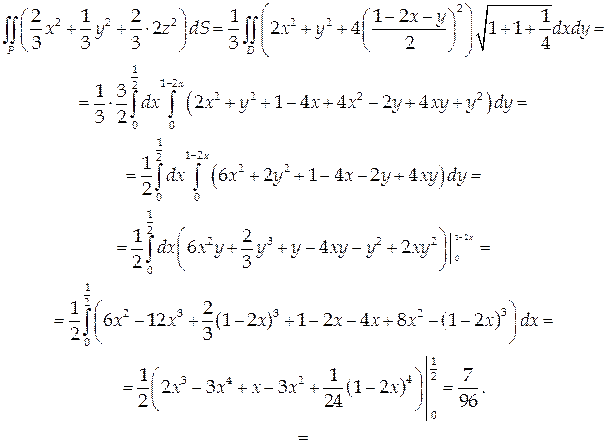
Дивергенцией векторного поля A = { Ax, Ay, Az }, где Ax, Ay, Az – функции от x, y, z, называется
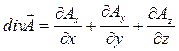. (57)
Пример 11.
Найти дивергенцию и ротор векторного поля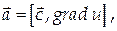 
где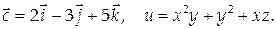 
Решение.
Найдем координаты вектора а:
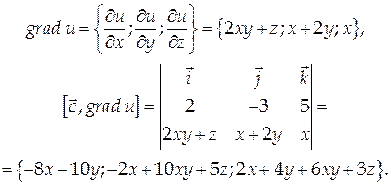
Тогда
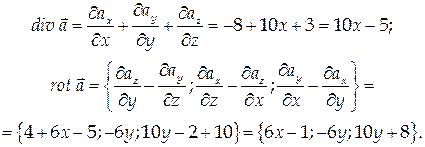
Векторное поле A = { Ax, Ay, Az } называется потенциальным, если вектор А является градиентом некоторой скалярной функции u = u(x, y, z):
A = grad u =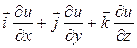 
. (58)
При этом функция и называется потенциалом данного векторного поля.
Пример 12.
Проверить, является ли векторное поле
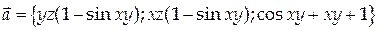
потенциальным, и в случае положительного ответа найти потенциал и, считая, что в начале координат он равен нулю.
Решение.
Поле является потенциальным, если выполнены следующие условия:
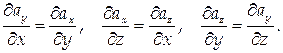
В нашем случае
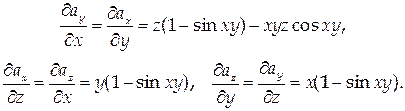
Следовательно, поле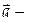 
потенциальное. Найдем его потенциал и, считая, что и (0;0;0) = 0:
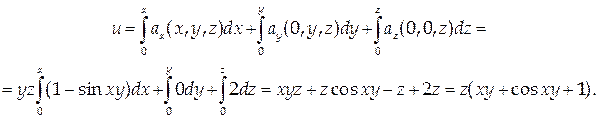
Векторное поле A = { Ax, Ay, Az } называется соленоидальным в области D, если в каждой точке этой области
div A = 0. (59)
|
|
|
