Опыт Штерна и Герлаха. Эффект Зеемана

7.1. В опытах Штерна и Герлаха узкий пучок атомов серебра (в нормальном состоянии) проходит через поперечное резко неоднородное магнитное поле и попадает на экран, находящийся на расстоянии b =20см от магнита. При каком значении градиента индукции магнитного поля расщепление пучка на экране Δz =2мм? Скорость атомов V =300м/с, протяженность магнита а =10см.

7.2. В одном из опытов по расщеплению узкого пучка по методу Штерна и Герлаха использовали атомы ванадия в основном состоянии ⁴F_3/2. Найти расстояние между крайними компонентами пучка на экране, если протяженность магнита а =10см, а расстояние от магнита до экрана b =20см; 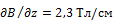и кинетическая энергия атомов Т =4·10⁴ эВ.

7.3. Пучок атомов рубидия в нормальном состоянии пролетает со скоростью υ =400 м/с через неоднородное магнитное поле с градиентом магнитной индукции .

Расщепление пучка на расстоянии 10 см от места выхода из магнитного поля равно 3,5 мм; протяженность магнитного поля равна 4 см. Найти спиновое квантовое число.

7.4. Атом находится в магнитном поле с индукцией В =0,3 Тл. Определить:

а) полное расщепление в электрон-вольтах терма ¹D;

б) спектральный символ синглетного терма, полная ширина расщепления которого составляет 104 мкэВ.

7.5. Построить схему возможных переходов в магнитном поле между следующими состояниями: а) ¹D → ¹Р, б) ¹F → ¹D. Сколько компонент содержит спектральная линия, соответствующая каждому из этих двух переходов?

7.6. Интервал между крайними компонентами спектральной линии λ =525 нм, обнаруживающей простой эффект Зеемана, составляет Δλ =22 пм. Найти интервал в электрон-вольтах между соседними подуровнями зеемановского расщепления соответствующих термов.

7.7. Построить схему возможных переходов в магнитном поле между термами ²Р_3/2 и ²S_1/2 в слабом магнитном поле. Вычислить для соответствующей спектральной линии:

а) смещения зеемановских компонент в единицах ; б) интервал частот Δω между крайними компонентами, если индукция магнитного поля В =0,5 Тл.

 

7.8. Изобразить схему возможных переходов в слабом магнитном поле и вычислить смещение (в единицах ) зеемановских компонент спектральной линии:

а) ²D_3/2 → ²Р_3/2 ,б) ²F_5/2 → ²D_3/2.

 

Рентгеновское излучение

8.1. Определить напряжение на рентгеновской трубке с никелевым антикатодом, если разность длин волн К_α -линии и коротковолновой границы сплошного рентгеновского спектра равна 84 пм.

8.2. При увеличении напряжения на рентгеновской трубке от U₁ =10 кВ до U₂ =20 кВ разность длин волн К_α -линии и коротковолновой границы сплошного рентгеновского спектра увеличилась в η =3 раза. Какой элемент используется в качестве антикатода?

8.3. Найти длину волны К_α -линии меди (Z =29), если известно, что длина волны К_α -линии железа (Z =26) равна 193 пм.

8.4. Вычислить с помощью закона Мозли:

а) длину волны К_α -линии алюминия и кобальта;

б) разность энергий связи К -и L -электронов ванадия.

8.5. Найти коротковолновую границу непрерывного рентгеновского спектра для случаев, когда к рентгеновской трубке приложена разность потенциалов: а) 30 кВ; б) 40 кВ; в) 50 кв.

8.6. Какое наименьшее напряжение надо приложить к рентгеновской трубке, чтобы получить все линии К -серии, если в качестве материала антикатода взять:

а) медь; б) серебро; в) вольфрам; г) платину?

8.7. Вычислить постоянную экранирования для линии К_α и К_β в характеристическом спектре хрома, если соответствующие длины волн равны 0,229 нм и 0,208 нм.

8.8. Найти коротковолновую границу сплошного рентгеновского спектра, если известно, что уменьшение приложенного к рентгеновской трубке напряжение на 23 кВ увеличивает искомую длину волны в 2 раза.

8.9. При переходе электрона в атоме с L - оболочки на K -оболочку излучается волна длиною 0,079 нм. Какой это атом?

8.10. Определить длину волны головной линии L - серии характеристического спектра платины, Z =78.

8.11. Определить длину волны К_α - линии характеристического рентгеновского спектра, получаемого в рентгеновской трубке с молибденовым антикатодом. Можно ли получить эту линию спектра, подав на рентгеновскую трубку напряжение 4 кВ?

8.12. У некоторого легкого элемента длины волн К_α - и К_β – линий равны λ_α=275пм и λ_β=251пм. Чему равна длина волны головной линии его L -серии? Что это за элемент?

8.13. Длина волны К_α - линии ниобия (Z =41) равна λ₁=76пм. Определить, какому элементу принадлежит линия К_α с длиной волны λ₂=251пм.

8.14. Вычислить наибольшую длину волны в K -серии характеристического рентгеновского излучения скандия (Z =21).

8.15. Определить значение наименьшей длины волны рентгеновского излучения, если к рентгеновской трубке приложено напряжение 30 кВ.

8.16. Найти длину волны коротковолновой границы сплошного рентгеновского спектра, если скорость электронов, подлетающих к аноду рентгеновской трубки υ =0,85с (с - скорость света в вакууме).

 

Молекулярные спектры

 

9.1. Исходя из выражения для вращательной энергии двухатомной молекулы, показать, что интервалы (в волновых числах) между спектральными линиями чисто вращательного спектра имеют одинаковую величину.

9.2. Определить интервалы (в см^-1) между соседними линиями в чисто вращательном спектре молекул HBr (расстояние между ядрами d =1,413∙10^-8 см).

9.3. Найти расстояние между ядрами молекулы CH, если известно, что интервалы между соседними линиями чисто вращательного спектра данной молекулы равны приблизительно 29 см^-1.

9.4. Найти механический момент молекулы кислорода, вращательная энергия которой E =2,16 мэВ, а расстояние между ядрами d =121 пм.

9.5. Найти для молекулы HCl вращательные квантовые числа двух соседних уровней, разность энергий которых 7,86 мэВ. Расстояние между ядрами d =127,5 пм.

9.6. Определить, на какую величину изменяется момент молекулы CO при испускании спектральной линии λ =1,29 мм, принадлежащей чисто вращательному спектру.

9.7. Определить угловую скорость вращения молекулы S₂, находящейся на первом возбужденном вращательном уровне, если расстояние между ее ядрами d =189 пм.

9.8. Сколько линий содержит чисто вращательный спектр молекул OH?

 

Радиоактивность

 

10.1. Активность некоторого препарата уменьшается в 2,5 раза за 7 суток. Найти его период полураспада.

10.2. В начальный момент активность некоторого радиоизотопа составляла 650 част/мин. Какова будет активность этого препарата по истечении половины его периода полураспада?

10.3. Препарат U²³⁸ массой 1,0г излучает 1,24·10⁴ α-частиц в секунду. Найти период полураспада этого изотопа и активность.

10.4. Вычислить удельные активности изотопов Na²⁴ и U²³⁵, периоды полураспада которых равны соответственно 15 часов и 7,1·10⁸лет.

10.5. В кровь человека ввели небольшое количество раствора, содержащего радиоизотоп Na²⁴ активностью А =2·10³расп/с. Активность 1см³ крови, взятой через t =5ч, оказалась А₁ =16 расп./(мин·см³). Период полураспада данного радиоизотопа T =15ч. Найти объем крови человека.

10.6. Вычислить постоянную распада, среднее время жизни и период полураспада радиоактивного ядра, активность которого уменьшается в 1,07 раза за 100 суток.

10.7. Определить количество свинца, возникающего из 1 кг чистого изотопа U²³⁸ за период, равный возрасту Земли (2,5·10⁹ лет). Период полураспада данного изотопа урана 4,5·10⁹ лет.

10.8. Единица радиоактивности кюри соответствует тому числу распадов, которое испытывает 1 г радия в течение одной секунды. Найти это число, зная, что период полураспада радия равен 1590 лет.

10.9. Какая доля первоначального количества ядер ⁹⁰Sr а) останется через 10 и 100 лет; б) распадется за 1 сутки; за 15 лет?

10.10. За сутки активность ядра уменьшилась в 16 раз. Определить период полураспада этого ядра.

10.11. Что больше - среднее время жизни τ радиоактивного ядра или период полураспада Т? Во сколько раз?

10.12. Чтобы определить возраст t древней ткани, была определена концентрация в ней атомов радиоуглерода ¹⁴С. Она оказалась соответствующей 9,2 распадам в минуту на один грамм углерода. Концентрация ¹⁴С в живых растениях соответствует 14,0 распадам в минуту на один грамм углерода. Период полураспада ¹⁴С равен 5730 лет. Исходя из этих данных, оценить t.

10.13. Определить возраст древних деревянных предметов, у которых удельная активность ¹⁴C составляет η =0,6 удельной активности этого же нуклида в только что срубленных деревьях. Период полураспада ¹⁴С равен 5730 лет.

10.14. Активность некоторого препарата уменьшилась в 256 раз. Скольким периодам полураспадам равен протекший промежуток времени?

10.15. Изотоп U²³⁸ массой 1 г, испускает 12200 α- частиц за 1 с. Рассчитать период полураспада.

10.16. Определить период полураспада радона, если за одни сутки из 1 млн. атомов распадается 175000 атомов.

10.17. Показать, что среднее время жизни радиоактивных ядер (λ – постоянная распада).

10.18. Первоначальная масса радиоактивного изотопа натрия (с периодом полураспада Т =62 с) равна 0,3 мг. Определить начальную активность изотопа и его активность через 5 минут.

 

Энергия связи

 

11.1. Выразить в единицах МэВ массу покоя электрона и атомную единицу массы. В чем отличие физической шкалы атомных масс от химической?

11.2. Вычислить энергию, необходимую для разделения ядра Ne²⁰ на две α-частицы и ядро C¹², если известно, что энергия связи на один нуклон в ядрах Ne²⁰ ; He⁴; C¹² равны соответственно 8,03; 7,07 и 7,68 МэВ.

11.3. Определить наименьшую энергию, необходимую для разделения ядра ¹²C₆ на 3 одинаковые части. Массы ядер углерода и гелия равны, соответственно 12,00000 а.е.м, 4,00260 а.е.м.

11.4. Найти с помощью табличных значений масс атомов:

а) среднюю энергию связи на один нуклон в ядре О¹⁶;

б) энергию связи нейтрона и α-частицы в ядре В¹¹;

в) энергию, необходимую для разделения ядра О¹⁶на четыре одинаковых части.

11.5. Рассчитать удельную энергию связи U²³⁸.

11.6. Какую энергию в киловатт-часах можно получить от деления 1 г ₉₂U²³⁵, если при каждом делении выделяется энергия 200 МэВ?

11.7. Найти энергию связи ядра атома гелия ₂He⁴.

11.8. Найти энергию связи ядра изотопа ₃Li⁷.

11.9. Найти энергию связи ядра атома алюминия ₁₃ Al²⁷.

11.10. Найти энергию связи ядра атома дейтерия ₁H².

 

 

Ядерные реакции

 

12.1. Покоящееся ядро ²¹³Ро испустило α-частицу с кинетической энергией К_α =8,34 МэВ. При этом дочернее ядро оказалось непосредственно в основном состоянии. Какую долю этой энергии составляет кинетическая энергия дочернего ядра? Какова скорость дочернего ядра?

12.2. Вычислить кинетическую энергию α-частицы, испускаемой при превращении урана-232 в торий-228 (масса урана 232,03714 а.е.м.). Найти кинетическую энергию тория.

12.3. Найти энергию, выделяющуюся при ядерных реакциях:

1) ₁H²+₁H²→₁H¹+₁H³, 2) ₁H²+₁H² →₂H³+₀n¹.

12.4. Найти энергию, освобождающуюся при ядерной реакции:

.

12.5. Вычислить с помощью законов сохранения лептонного и барионного заряда, возможны ли следующие реакции:

а) в)

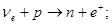б) г)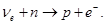

12.6. Определить порядковый номер и массовое число изотопа, который получается из тория ₉₀Th²³² после трех α- и двух β-превращений.

12.7. Какой изотоп образуется из U²³⁸ после трех α-распадов и двух β-распадов?

12.8. Определить энергию, которая выделится при аннигиляции электрона и позитрона, если масса покоя электрона 9,1·10^-31кг?

12.9. При реакции деления ядер урана U²³⁵ выделилось 1,204·10²⁶МэВ энергии. Определить массу распавшегося урана, если при делении одного ядра выделяется 200 МэВ энергии.

12.10. Нейтрон и антинейтрон соединяются, образуя два фотона. Найти энергию каждого из возникших фотонов, считая, что начальная энергия частиц ничтожно мала.

12.10. Электрон и позитрон, имевшие одинаковые кинетические энергии, равные 0,24 МэВ, при соударении превратились в два одинаковых фотона. Определить энергию каждого фотона и соответствующую ему длину волны.

12.12. Фотон с энергией 3 МэВ превратился в пару электрон-позитрон. Определить кинетическую энергию каждой частицы, считая ее одинаковой.

12.13. При бомбардировке ₃Li⁶ дейтронами (ядро дейтерия ₁Н²) образуются две α- частицы, разлетающиеся симметрично под углом α, к направлению налетающих дейтронов. а) Найти кинетическую энергию образующихся α- частиц, если энергия налетающих дейтронов равна 0,2 МэВ. б) Найти угол α.

12.14. Считая, что в одном акте деления ядра урана-235 освобождается энергия 200 МэВ, определить энергию, выделяющуюся при сгорании 1 кг этого изотопа и массу каменного угля с удельной теплотой сгорания 30 кДж/г, эквивалентную в тепловом отношении 1 кг изотопа U²³⁵.

12.15. Как определяются значения энергии, освобождаемой при β^- - распаде, β⁺ -распаде и К-захвате, если известны массы материнского и дочернего атомов и масса электрона?

12.16. Вычислить максимальное значение импульса электронов, испускаемых ядрами ¹⁰Be, если известно, что дочерние ядра оказываются непосредственно в основном состоянии.

12.17. Найти энергию реакции ⁷Li(p,α)⁴He, если известно, что средняя энергия связи на 1 нуклон в ядрах ⁷Li и ⁴He равна соответственно 5,60 и 7,06 МэВ.

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: