 |
Тест № 8. Линейная функция и её график.
|
|
|
|
Вариант 1
Часть А
А 1. Среди данных функций укажите все функции,
являющиеся линейными:
1) у = 4 +2х; 2) у = х  - 3; 3) у = 6х; 4) у =
- 3; 3) у = 6х; 4) у = 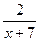 ;
;
5) у = 3; 6) у =  - 4.
- 4.
а) 1; 3; 4 б) 1; 3; 6 в) 1; 3; 5; 6
А 2. Найдите значение функции у = -0,5х - 2, если
значение аргумента равно -2,4.
а) -3,2 б) -0,8 в) 0,8
А 3. Принадлежит ли графику функции у = 2х + 4 точка
А(-2;0)?
а) да б) нет в) не знаю
А 4. Найдите точку пересечения графиков функций
у = 0,5х + 1 и у = -х + 4. В ответе укажите сумму
координат этой точки.
а) 4 б) 1,3 в) 1,75
Часть В.
Найдите линейную функцию, график которой проходит через точки А(0;2) и В(-2;1).
Вариант 2
Часть А
А 1. Среди данных функций укажите все функции,
являющиеся линейными:
1) у = 3 - 7х; 2) у = х  + 2; 3) у = х; 4) у =
+ 2; 3) у = х; 4) у =  ;
;
5) у = 5; 6) у =  + 1.
+ 1.
а) 1; 3; 4 б) 1; 3; 6 в) 1; 3; 5; 6
А 2. Найдите значение функции у = -0,2х + 2, если
значение аргумента равно 1,2.
а) 1,76 б) -0,4 в) -0,22
А 3. Принадлежит ли графику функции у = -2х + 8 точка
В(1;4)?
а) да б) нет в) не знаю
А 4. Найдите точку пересечения графиков функций
у = 4х - 3 и у = -х + 7. В ответе укажите сумму
координат этой точки.
а) -7 б) 9 в) 7
Часть В.
Найдите линейную функцию, график которой проходит через точки А(1;3) и В(0;4).
Тест № 9. Взаимное расположение графиков линейных функций
Вариант 1
Часть А
А 1. Выберите пару функций, графики которых
параллельны:
1) у = 5 + 3х; 2) у = 5х + 3; 3) у = 3; 4) у = 3х.
а) 2 и 3 б) 1 и 2 в) 1 и 4
А 2. Найдите значение а, если известно, что график
функции у = 2х + а проходит через точку А(-2; -6):
а) -2 б) 10 в) -10
А 3. Выберите уравнение прямой, которая параллельна
прямой у = 4х – 3 и пересекает ось Оу в точке А(0; -2).
а) у = 4х - 2 б) у = 4х + 2 в) у = -2х + 4
А 4. Найдите координаты точки пересечения графиков
|
|
|
функций у =  х – 3 и у =
х – 3 и у = 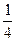 х + 2.
х + 2.
а) (8; 90) б) (8; 80) в) (60; 17)
Часть В
Определите формулу функции, график которой параллелен прямой у = 2х и проходит через точку А(4; -3).
Вариант 2
Часть А
А 1. Выберите пару функций, графики которых
параллельны:
1) у = - 4х; 2) у = 5х + 5; 3) у = - 4; 4) у = 5х - 4.
а) 1 и 3 б) 3 и 4 в) 2 и 4
А 2. Найдите значение k, если известно, что график
функции у = kх - 4 проходит через точку С(4; -8):
а) -3 б) -1 в) 1
А 3. Выберите уравнение прямой, которая параллельна
прямой у = 3х – 2 и пересекает ось Оу в точке А(0; 4).
а) у = 3х - 4 б) у = 3х + 4 в) у = -3х + 4
А 4. Найдите координаты точки пересечения графиков
функций у = 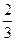 х + 3 и у =
х + 3 и у =  х - 2.
х - 2.
а) (6; 7) б) (-6; -11) в) (-1,2; -3,8)
Часть В
Определите формулу функции, график которой параллелен прямой у = -0,4х и проходит через точку А(-5; 3).

Тест № 10. Определение степени с натуральным показателем
Вариант 1
Часть А
А 1. Представьте произведение в виде степени:
1) 16 ∙ 16 ∙ 16
а) 16 ∙ 3 б) 16  в) 4096
в) 4096
2) b ∙ b ∙ b ∙ b ∙ b
а) b  б) 5b в) 5 + b
б) 5b в) 5 + b
3) -0,5 ∙ (-0,5) ∙ (-0,5) ∙ (-0,5)
а) -0,5 ∙ 4 б) (-0,5)  в) -0,5
в) -0,5 
А 2. Упростите выражение:
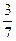 ∙
∙ 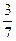 ∙ 5 ∙ 5 ∙ 5 ∙
∙ 5 ∙ 5 ∙ 5 ∙ 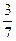 ∙
∙ 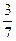
а) 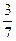 ∙ 4 ∙ 5 ∙ 3 б) 5
∙ 4 ∙ 5 ∙ 3 б) 5  ∙ (
∙ (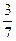 )
)  в) 5
в) 5  ∙
∙ 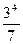
А 3. Вычислить:
1) (-3)  ∙ 2
∙ 2
а) (-6)  б) -162 в) 162
б) -162 в) 162
2) - 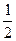 ∙ (-3)
∙ (-3) 
а) 3  б) 13,5 в) – 13,5
б) 13,5 в) – 13,5
3) -2 
а) – 16 б) 16 в) – 8
А 4. Найдите значение выражения:
1,5 ∙ 8  - 5
- 5 
а) – 29 б) 19 в) 49
А 5. Найдите значение выражения:
1 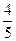 : (-
: (-  )
)  + 3 ∙ (-
+ 3 ∙ (- 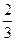 )
) 
а) – 7,5 б) – 7 в) -7 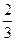
Часть В
Не выполняя вычислений, расположите в порядке возрастания следующие числа: (0,3)  ; (-1,2)
; (-1,2)  ; (1,5)
; (1,5)  ; (- 4)
; (- 4)  .
.

Вариант 2
Часть А
А 1. Представьте произведение в виде степени:
1) 11 ∙ 11 ∙ 11 ∙ 11
а) 11 ∙ 4 б) 11  в) 14641
в) 14641
2) х ∙ х ∙ х ∙ х
а) х  б) 4х в) 4 + х
б) 4х в) 4 + х
3) (- 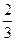 ) ∙ (-
) ∙ (- 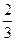 ) ∙ (-
) ∙ (- 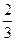 )
)
а) (- 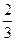 )
)  б) (-
б) (- 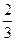 ) ∙ 3 в)
) ∙ 3 в) 
А 2. Упростите выражение:
 ∙
∙  ∙
∙  ∙ с ∙ с ∙ с ∙ с ∙ с
∙ с ∙ с ∙ с ∙ с ∙ с
|
|
|
а)  ∙ 5с б) (
∙ 5с б) ( )
)  ∙ с
∙ с  в)
в)  ∙ с
∙ с 
А 3. Вычислить:
1) (-2)  ∙ 3
∙ 3
а) (-6)  б) -96 в) 96
б) -96 в) 96
2) -  ∙ (-2)
∙ (-2) 
а) (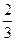 )
)  б)
б) 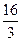 в) – 5
в) – 5 
3) -7 
а) – 49 б) 49 в) – 14
А 4. Найдите значение выражения:
(0,6 ∙ 5  - 15)
- 15) 
а) 144 б) 36 в) 3600
А 5. Найдите значение выражения:
6 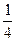 ∙ 0,2
∙ 0,2  - (1
- (1 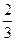 )
)  ∙ 1,08
∙ 1,08
а) – 4,25 б) – 4,75 в) – 4,5
Часть В
Не выполняя вычислений, расположите в порядке возрастания следующие числа: (1,3)  ; (-0,4)
; (-0,4)  ; (0,9)
; (0,9)  ; (- 3)
; (- 3)  .
.

Тест № 11. Свойства степени с натуральным показателем
Вариант 1 Часть А
А 1. Упростить выражение: х  ∙ (х
∙ (х  )
) 
а) х  б) х
б) х  в) х
в) х 
А 2. Для каждого выражения в верхней строке укажите
равное ему выражение в нижней строке:
1) (а  )
)  2)
2)  3)
3) 
а) а  б)
б)  в) а
в) а 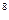
А 3. Вычислить: 1) 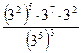
а) 81 б) 3 в) 9
2)  а) 14
а) 14  б) 14 в) 196
б) 14 в) 196
А 4. Упростить выражение: 
а) а  б) а
б) а  в) а
в) а 
Часть В
Вычислить: 

Вариант 2 Часть А
А 1. Упростить выражение: х  ∙ (х
∙ (х  )
) 
а) х  б) х
б) х  в) х
в) х 
А 2. Для каждого выражения в верхней строке укажите
равное ему выражение в нижней строке:
1) ( )
)  2)
2) 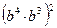 3) b
3) b 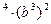
а) b  б)
б)  в) b
в) b 
А 3. Вычислить: 1) 
а) 32 б) 256 в) 2 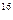
2)  а) 15
а) 15  б) 225 в) 15
б) 225 в) 15 
А 4. Упростить выражение: 
а) m  б) m
б) m 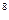 в) m
в) m 
Часть В
Вычислить: 
Тест № 12. Одночлен и его стандартный вид. Умножение одночленов. Возведение одночлена в степень
Вариант 1
Часть А
А 1. Представьте одночлен в стандартном виде:
1) a ∙ 3аb
а) 4а  б) 3а
б) 3а  в) 4аb
в) 4аb
2) (-3) 
а) -18a 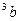 б) 18a
б) 18a 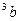 в) a
в) a 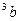 ∙ (-12)
∙ (-12)
А 2. Найдите площадь прямоугольника со сторонами
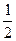 а и 10а.
а и 10а.
а) 10,5а б) 5а  в) 10,5а
в) 10,5а 
А 3. Найдите площадь квадрата со стороной 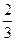 а.
а.
а) 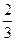 а
а  б)
б)  а
а  в)
в)  а
а
А 4. Выберите среди данных выражений все одночлены:
1) а + b 2) ab 3) 7 4)  5) х
5) х 
а) 1; 2; 5 б) 2; 3; 5 в) 2; 4; 5
А 5. Выполните действия:
1) (2а)  ∙ (- 2а)
∙ (- 2а)
а) – 8а  б) – 4а
б) – 4а  в) 8а
в) 8а 
2) (- а)  ∙ (3аb
∙ (3аb  )
)
а) 3а  b
b  б) - 3а
б) - 3а  b
b  в) 3а
в) 3а  b
b 
3) (- 2 b  с)
с)  ∙ (- 2bс
∙ (- 2bс  )
) 
а) – 32b 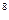 с
с  б) 24b
б) 24b 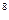 с
с  в) - 4b
в) - 4b 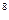 с
с 
А 6. Представить одночлен в виде квадрата или куба
другого одночлена:
1) 4а 
а) (4а)  б) (2а)
б) (2а)  в) 2а
в) 2а 
2)  а
а  b
b 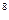
а) ( а
а  b
b  )
)  б) (
б) ( а
а  b
b  )
)  в)
в)  (а
(а  b
b  )
) 
3) – 0,001х  у
у 
а) (- 0,1х  у
у  )
)  б) (- 0,1х
б) (- 0,1х  у
у  )
)  в) – 0,001(х
в) – 0,001(х  у
у  )
) 
Часть В
Заполните звёздочку такими одночленами стандартного вида, чтобы выполнялось равенство:
 а) 6х
а) 6х  у ∙ * = -3,6х
у ∙ * = -3,6х  у
у  б) (*)
б) (*)  ∙ (*)
∙ (*)  = - 256х
= - 256х  у
у 

Вариант 2
Часть А
А 1. Представьте одночлен в стандартном виде:
|
|
|
1) ху ∙ 2х
а) х  б) 2х
б) 2х  в) 3ху
в) 3ху
2) 3 
а) - 6a 
 б) a
б) a 
 ∙ (- 6) в) – 6а
∙ (- 6) в) – 6а  b
b
А 2. Найдите площадь прямоугольника со сторонами
5а и 0,5а.
а) 2,5а  б) 2,5а в) 5,5а
б) 2,5а в) 5,5а
А 3. Найдите площадь квадрата со стороной 0,5а.
а) 0,25а  б) 0,5а
б) 0,5а  в) а
в) а
А 4. Выберите среди данных выражений все одночлены:
1) 3аb 2) 8 3) 2а + 3с 4)  5) 6х
5) 6х 
а) 1; 2; 5 б) 2; 3; 5 в) 2; 4; 5
А 5. Выполните действия:
1) (- 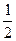 b)
b)  ∙ 2b
∙ 2b
а) 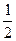 b
b  б) –
б) – 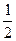 b
b  в)
в) 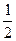 b
b 
2) 2а  b ∙ (- а)
b ∙ (- а) 
а) 2а  b б) - 2а
b б) - 2а  b в) 2а
b в) 2а  b
b
3) (2 ху  )
)  ∙ (- 2х
∙ (- 2х  у)
у) 
а) – 32х  у
у 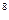 б) 32х
б) 32х  у
у  в) 4х
в) 4х  у
у 
А 6. Представить одночлен в виде квадрата или куба
другого одночлена:
3) 8а 
а) (8а)  б) 2а
б) 2а  в) (2а)
в) (2а) 
2)  b
b  с
с 
а) (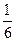 b
b  с
с  )
)  б) (
б) (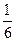 b
b  с
с  )
)  в)
в)  (b
(b  с
с  )
) 
3) – 0,008а  b
b 
а) (- 0,2а  b)
b)  б) (- 0,2а
б) (- 0,2а  b)
b)  в) – 0,008(а
в) – 0,008(а  b)
b) 
Часть В
Заполните звёздочку такими одночленами стандартного вида, чтобы выполнялось равенство:
 а) * ∙ 4а
а) * ∙ 4а  b
b  = 0,16а
= 0,16а  b
b  б) (*)
б) (*)  ∙ (*)
∙ (*)  = 128с
= 128с  d
d 
 |
|
|
|


