 |
Определение кинематических передаточных функций
|
|
|
|
Кинематическими характеристиками являются: перемещение, траектории движения, скорости звеньев и характерных точек механизма. Задачу определения кинематических характеристик решим графо-аналитическим методом, который основан на построении ряда последовательных положений звеньев механизма и соответствующих им планов скоростей.
Механизм привода пресс-автомата с плавающим ползуном в масштабе μL=0,006 м/мм изобразим в двенадцати положениях. Положение механизма задаётся положением кривошипа 1. Каждое последующее положение кривошипа 1 отличается от предыдущего на 30ْ. Первое, крайнее, положение механизма соответствует началу рабочего цикла. В каждом из положений определим линейные скорости кинематических пар, центров тяжести весомых звеньев, а также угловые скорости звеньев. Угловую скорость кривошипа 1 будем считать, в соответствии с исходными данными, постоянной и равной единице, так как необходимые необходимые кинематические передаточные функции представляют собой отношения соответствующих линейных и угловых скоростей к угловой скорости ведущего звена, т.е. мы сразу находим кинематические передаточные функции.
Вектор скорости точки в сложном движении представим в виде суммы двух векторов: вектора скорости точки, принятой за полюс и вектора скорости точки в относительном движении.
В качестве примера рассмотрим построение плана скоростей для третьего положения механизма (Рисунок 5). Сначала выберем масштаб μv=0,0007 (м/с)/мм, затем выберем полюс P3, от которого в выбранном масштабе будем откладывать векторы линейных скоростей.
Определим линейные скорости точек А, В2, В4, С, Е и угловые скорости звеньев: второго звена (шатун 2)ω2 и пятого (кулиса 5) ω5.
|
|
|
Из полюса P3, перпендикулярно отрезку О1А откладываем в выбранном масштабе вектор V А линейной скорости точки А, для этого воспользуемся формулой
lvi =V/μv, (1)
где V – скорость точки (м/с), μv – масштаб вектора скорости ((м/с)/мм).
V=μv*lvi
На плане скоростей вектору V А соответствует вектор а. Величина вектора V А будет одинакова для всех положений механизма и равна:
V А=ω1 *l 1 =1рад*0,05м=0,05 (м/с).
На плане скоростей из полюса P3 отложим вектор а длиной:
а= V А/ μv=0,05/0,0007=71,5 мм.
Далее для определения скорости точки С воспользуемся векторным равенством:
V С= V А+ V СА, (2)
где V С – абсолютная скорость точки С, вектор, который перпендикулярен кулисе 5, V А– линейная скорость точки А (известная и по величине и по направлению), V СА – вектор скорости точки С, принадлежащей кулисе 5, в относительном вращательном движении шатуна 2 вокруг полюса А. Вектор скорости V СА перпендикулярен отрезку СА. Для построения вектора V С, которому на плане скоростей соответствует вектор с, через конец вектора а проведём прямую, перпендикулярную отрезку АС, на ней будет расположен вектор V СА,которому на плане скоростей соответствует вектор са. Далее из полюса P3 проводим прямую, параллельную вектору скорости точки С (перпендикулярно О2С). Пересечение этих двух прямых задаст оба искомых вектора, модули которых будут равняться:
V С= μv* с =0,0007*67=0,0469 (м/с), V СА = μv* са =0,0007*43=0,0301 (м/с).
Теперь зная скорость V СА, можно найти угловую скорость звена АС (шатуна 2):
ω2= V СА/ l 2 =0,0301/0,6=0,05 (рад/с).
Зная ω2, найдём скорость точки В2 с помощью выражения
VB 2 = V А+ VB 2А, (3)
где VB 2 – абсолютная скорость точки В2, V А – линейная скорость точки А, VB 2А – скорость точки В2 в относительном движении.
Вектор скорости VB 2А перпендикулярен отрезку АС. Так как направление вектора
|
|
|
VB 2А перпендикулярно отрезку АС, а его модуль равен
VB 2А =ω2*l АВ =0,05*0,3=0,015
(м/с), то необходимо из конца вектора а на плане скоростей отложить отрезок длиной b 2 a = VB 2А /μv=0,015/0,0007=21,4 (мм) (вектору VB 2А на плане скоростей соответствует вектор b 2 a) и соединить его конец с полюсом P3. Полученный вектор b 2 является вектором скорости точки В2 - VB 2, модуль которого равен:
VB 2 =μv* b 2 =0,0007*65=0,0455 (м/с).
Скорость точки Е можно определить по принадлежности кулисе 5, которая совершает возвратно-вращательное движение:
V Е =ω5*l О2Е, (4)
Угловую скорость кулисы 5 найдём из выражения:
ω5= V С /l О2С =0,0469/0,21=0,22 (рад/с),
следовательно, V Е =0,22*0,105=0,0234 (м/с). На плане скоростей вектору V Е будет соответствовать вектор е, длина которого равна: е= V Е /μv=0,0234/0,0007=33,45 (мм). Вектор е сонаправлен с вектором с.
Для определения скорости точки В4 воспользуемся векторным уравнением:
VB 4 = VB 2+ VB 4 B 2, (5)
где VB 4 – абсолютная скорость точки В4 (векторы скоростей всех точек, принадлежащих пуансону 4, совпадают, так как это звено совершает поступательное движение), VB 2 – скорость точки В2 (полюса), VB 4 B 2 – скорость точки В4 в поступательном движении относительно точки В2.
В соответствии с данным уравнением через конец вектора b 2 проведём параллельно направляющей В2В4 вертикальную прямую, а из полюса P3 – горизонтальную, параллельно штанге. Пересечение этих прямых задаёт векторы абсолютной b 4 (VB 4) и относительной b 4 b 2 (VB 4 B 2) скоростей.
Значение скоростей равны:
VB 4 =μv* b 4 =0,0007*63=0,0441 (м/с),
VB 4 B 2 = μv* b 4 b 2 =0,0007*14=0,01 (м/с).
Аналогично построим планы скоростей для всех остальных положений механизма 1…12 (Рисунок 4…9). Все найденные значения относительных угловых и относительных линейных скоростей представлены в Таблице 2. Изменение относительных линейных и угловых скоростей представлены в виде графиков на Рисунках 10, 11.
Таблица 2. Значения кинематических передаточных функций механизма в зависимости от угла поворота кривошипа.
| № положения | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 1 | ||
| φ, рад | 0 | π/6 | π/3 | π/2 | 2π/3 | 5π/6 | π | 7π/6 | 4π/3 | 3π/2 | 9π/3 | 11π/6 | 2π | ||
| VА / ω1, м | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 | ||
| VB2 / ω1, м
| 0,025 | 0,032 | 0,046 | 0,05 | 0,043 | 0,031 | 0,025 | 0,037 | 0,045 | 0,05 | 0,046 | 0,036 | 0,025 | ||
| VС / ω1, м | 0 | 0,024 | 0,047 | 0,05 | 0,041 | 0,022 | 0 | 0,027 | 0,041 | 0,05 | 0,044 | 0,028 | 0 | ||
| VЕ / ω1, м | 0 | 0,012 | 0,023 | 0,025 | 0,02 | 0,011 | 0 | 0,014 | 0,021 | 0,025 | 0,022 | 0,014 | 0 | ||
| VB4 / ω1, м | 0 | 0,025 | 0,044 | 0,05 | 0,042 | 0,024 | 0 | 0,028 | 0,042 | 0,05 | 0,043 | 0,027 | 0 | ||
| ω 2 / ω1 | 0,083 | 0,082 | 0,05 | 0 | 0,051 | 0,079 | 0,083 | 0,068 | 0,035 | 0 | 0,035 | 0,062 | 0,083 | ||
| ω 5 / ω1 | 0 | 0,115 | 0,22 | 0,238 | 0,193 | 0,107 | 0 | 0,129 | 0,197 | 0,238 | 0,21 | 0,133 | 0 |
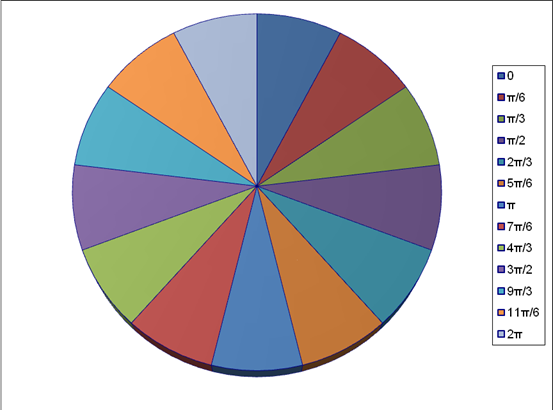
Рисунок 10. Зависимости относительных линейных скоростей характерных точек механизма от угла поворота кривошипа.
ряд 1 - V А / ω 1
ряд 2 - VB2 / ω 1
ряд 3 - VС / ω1
ряд 4 - VЕ / ω1
ряд 5 - VB4 / ω1
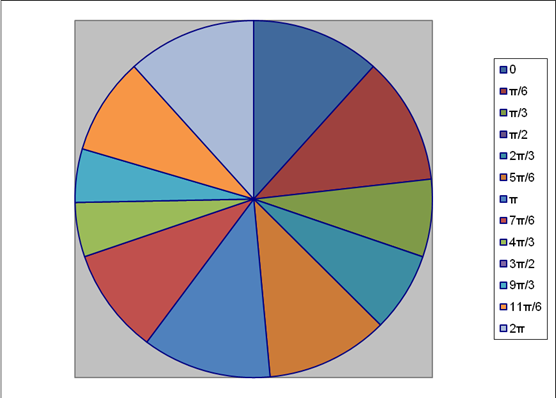
Рисунок 11. Зависимости относительных угловых скоростей звеньев механизма от угла поворота кривошипа
ряд 1 - ω 2 / ω1
ряд 2 – ω 5 / ω1
СИЛОВОЙ АНАЛИЗ МЕХАНИЗМА
Анализ нагруженности реального механизма представляет собой довольно сложную задачу. Для упрощения её решения в механизме с одной степенью свободы совокупность всех звеньев и усилий заменяют динамической моделью.
Динамическая модель представляет собой одно звено (звено приведения) с переменными инерционными характеристиками, находящиеся в равновесии под действием момента движущих сил, приложенного со стороны привода, и момента сил сопротивления, определяемого силами полезных и вредных сопротивлений. Так как природа этих усилий различна, то их целесообразно разделить на усилия, независимые от времени – силы статического сопротивления и усилия, связанные с переменностью движения звеньев – силы динамического сопротивления. Соответственно, момент движущих сил, приложенный к кривошипу, определяется двумя составляющими:
Мдв=Мст+Мдин, (1)
где Мдв – момент движущих сил;
Мст – момент движущих сил, предназначенный для преодоления сил статического сопротивления (статический момент);
Мдин – момент движущих сил, предназначенный для преодоления сил динамического сопротивления (динамический момент).
ОПРЕДЕЛЕНИЕ МОМЕНТА МСТ(Φ) ДЛЯ ПРЕОДОЛЕНИЯ СИЛ СТАТИЧЕСКОГО СОПРОТИВЛЕНИЯ
|
|
|
Используя теорему мощностей, можно записать формулу для расчёта статического момента, предназначенного для преодоления сил статического сопротивления:

где Fi – сила статического сопротивления, приложенная в i-ой точке механизма;
Vi – линейная скорость i-ой точки механизма;
ω1- угловая скорость кривошипа 1;
Fi^(Vi/ω1) – угол между вектором i-ой силы и вектором скорости точки её приложения;
n – число сил сопротивления статического характера.
Статический момент, предназначенный для преодоления сил статического сопротивления вычисляется по формуле:
Мст= - [ G 2 ·(VB 2/ω1)·cos(G 2, VB 2/ω1)+ G 3 ·(VB 2/ω1)·cos(G 3, VB 2/ω1) + G 4 · ·(VB 4/ω1)·cos(G 4, VB 4/ω1)+ G 5 ·(VE /ω1)·cos(G 5, VE /ω1)+ Q ·(VB 4/ω1) ·cos(Q, VB 4/ω1)], (3)
Третье слагаемое равно нулю, т.к. угол G 4, VB 4/ω1 равен 90ْ или 270ْ в зависимости от положения пуансона, следовательно, cos(G 4, VB 4/ω1)=0 во всех положениях.
Пятое слагаемое нужно записывать со знаком минус (угол Q, VB 4/ω1 =180ْ, cos180ْ =-1); оно не равно нулю в те моменты времени, когда пуансон выдавливает заготовку, следовательно, формула (3) примет вид:
Мст= - [ G 2 ·(VB 2/ω1)·cos(G 2, VB 2/ω1)+ G 3 ·(VB 2/ω1)·cos(G 3, VB 2/ω1)+ G 5 · ·(VE /ω1)·cos(G 5, VE /ω1)- Q ·(VB 4/ω1)], (4)
Значения углов между вектором i-ого усилия и вектором скорости i-ой точки приведены в таблице 3.
Таблица 3. Значения углов между вектором 1-ого усилия и вектором 1-ой точки.
| № положения | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 1 |
| φ, рад | 0 | π/6 | π/3 | π/2 | 2π/3 | 5π/6 | π | 7π/6 | 4π/3 | 3π/2 | 5π/3 | 11π/6 | 2π |
| G 2, VB 2/ ω 1 | 180 | 128 | 104 | 90 | 77 | 52 | 0 | 46 | 69,5 | 90 | 110 | 132 | 180 |
| G3,VB2/ω1 | 180 | 128 | 104 | 90 | 77 | 52 | 0 | 46 | 69,5 | 90 | 110 | 132 | 180 |
| G5,VE/ω1 | VE=0 | 79 | 84,5 | 90 | 98,5 | 102 | VE=0 | 78 | 82 | 90 | 97 | 101 | VE=0 |
Проведём расчёт Мст для каждого из выбранных положений механизма:
Мст1=-(2500·0,025·cos(180ْ)+800·0,025·cos(180ْ)+1500·0)=-(-62,5-20)=82,5 (н·м);
Мст2=-(2500·0,032·cos(128ْ)+800·0,032·cos(128ْ)+1500·0,012·cos(79ْ))=-(-49,25-15,76+3,43)=61,58 (н·м);
Мст3=-(2500·0,046·cos(104ْ)+800·0,046·cos(104ْ)+1500·0,023·cos(84,5ْ))=-(-27,82-8,9+3,31)=33,41 (н·м);
Мст4=-(2500·0,05·cos(90ْ)+800·0,05·cos(90ْ)+1500·0,025·cos(90ْ)-1750·0,05)=-(0+0+0-87,5)=87,5 (н·м);
Мст5=-(2500·0,043·cos(77ْ)+800·0,043·cos(77ْ)+1500·0,02·cos(98,5ْ)-5540·0,042)= -(24,18+7,74-4,43-232,68)=205,19 (н·м);
Мст6=-(2500·0,031·cos(52ْ)+800·0,031·cos(52ْ)+1500·0,011·cos(102ْ))=-(47,71+15,27-3,43)= -59,55 (н·м);
Мст7=-(2500·0,025·cos(0ْ)+800·0,025·cos(0ْ)+1500·0)=-(62,5+20)=-82,5 (н·м);
Мст8=-(2500·0,037·cos(46ْ)+800·0,037·cos(46ْ)+1500·0,014·cos(78ْ))=-(64,26+20,56+4,37)= -89,19 (н·м);
Мст9=-(2500·0,045·cos(69,5ْ)+800·0,045·cos(69,5ْ)+1500·0,021·cos(82ْ))= -(39,4+12,61+4,38)=-56,39 (н·м);
Мст10=-(2500·0,05·cos(90ْ)+800·0,05·cos(90ْ)+1500·0,025·cos(90ْ))=-(0+0+0)=0 (н·м);
Мст11=-(2500·0,046·cos(110ْ)+800·0,046·cos(110ْ)+1500·0,022·cos(97ْ))=-(-39,33-12,59-4,02)=47,9 (н·м);
Мст12=-(2500·0,036·cos(132ْ)+800·0,036·cos(132ْ)+1500·0,014·cos(101ْ))=-(-60,22-19,27-4,01)=75,48 (н·м);
|
|
|
Мст13=-(2500·0,025·cos(180ْ)+800·0,025·cos(180ْ)+1500·0)=-(-62,5-20)=82,5 (н·м).
ОПРЕДЕЛЕНИЕ МОМЕНТА МДИН (Φ) ДЛЯ ПРЕОДОЛЕНИЯ СИЛ ДИНАМИЧЕСКОГО СОПРОТИВЛЕНИЯ
Силы динамического сопротивления, действующие в механизме, также как и силы статического сопротивления могут быть приведены к кривошипу. Динамический момент найдём по формуле:
Мдин= ω 1²/2 ·d I пр/ d φ + ε 1 · I пр,(5)
где ω 1 – угловая скорость кривошипа;
ε 1 – угловое ускорение кривошипа;
φ – угол поворота кривошипа;
I пр – приведённый момент инерции механизма.
Т.к. угловая скорость кривошипа ω 1 постоянная, то ε 1 =0. Значит формулу (5) можно записать в виде:
Мдин= ω 1²/2 ·d I пр/ d φ,(6)
где величина ω 1²/2 =const, а ω 1 =2π·n1/60=2·3,14·140/60=14,65 рад, следовательно, ω 1²/2= 107,3113 рад².
Параметр I пр определяется формулой
I пр = ∑ (mi ·(Vi / ω 1)²+ Ii ·(ωi / ω 1)²), (7)
где mi – масса i-ого звена, mi = Gi / g;
Ii – момент инерции i-ого звенаотносительно полюса;
Vi / ω 1 и ωi / ω 1 – кинематические передаточные функции;
n – количество весомых звеньев.
Рассчитаем значения момента инерции (I пр) для каждого из положений механизма. Для нашего случая формулу (7) можно записать в следующем виде:
I пр =(m 2 ·(VB 2 / ω 1)²+ (m 2 ·(l 2)²/12 ) ·(ω 2 / ω 1)²)+((m 5 ·(l 5)²/3 ) · (ω 5 / ω 1)²) + m 4 · ·(VB 4 / ω 1)²+ m 3 ·(VB 2 / ω 1)², (8)
где m 2 = G 2 / g = 2500/9,8=255,1 (кг) – масса шатуна;
m 3 = G 3 / g = 800/9,8=81,6 (кг) – масса ползуна;
m 4 = G 4 / g = 1000/9,8=102 (кг) – масса пуансона;
m 5 = G 5 / g = 1500/9,8=153,1 (кг) – масса кулисы;
I 2= m 2 ·(l 2)²/12=255,1·(0,6)²/12=7,653 (кг·м²) – момент инерции шатуна;
I 5= m 5 ·(l 5)²/3=153,1·(0,21)²/3=2,251 (кг·м²) – момент инерции кулисы.
Подставив найденные значения m 2, m 3, m 4, I 2, I 5 (эти величины постоянные) в формулу (8), получим:
I пр =255,1·(VB 2 / ω 1)²+7,653·(ω 2 / ω 1)²+2,251·(ω 5 / ω 1)² + 102·(VB 4 / ω 1)²+81,6· ·(VB 2 / ω 1)², (9)
I пр =336,7·(VB 2 / ω 1)²+7,653·(ω 2 / ω 1)²+2,251·(ω 5 / ω 1)² + 102·(VB 4 / ω 1)², (9)
Проведём расчёт I пр для всех выбранных положений механизма по формуле (9):
I пр 1=336,7·(0,025)²+7,653·(0,083)²+2,251·(0)² + 102·(0)²=0,21+0,053=0,263 (кг·м²);
I пр 2=336,7·(0,032)²+7,653·(0,082)²+2,251·(0,115)² + 102·(0,025)²=0,345+0,052+0,030+ +0,064=0,491 (кг·м²);
I пр 3=336,7·(0,046)²+7,653·(0,05)²+2,251·(0,22)² + 102·(0,044)²=0,712+0,019+0,109+ +0,197=1,037 (кг·м²);
I пр 4=336,7·(0,05)²+7,653·(0)²+2,251·(0,238)² + 102·(0,05)²=0,842+0+0,128+0,255=1,225 (кг·м²);
I пр 5=336,7·(0,043)²+7,653·(0,051)²+2,251·(0,193)² + 102·(0,042)²=0,623+0,02+0,084+ +0,180=0,907 (кг·м²);
I пр 6=336,7·(0,031)²+7,653·(0,079)²+2,251·(0,107)² + 102·(0,024)²=0,324+0,048+0,026+ +0,059=0,457 (кг·м²);
I пр 7=336,7·(0,025)²+7,653·(0,083)²+2,251·(0)² + 102·(0)²=0,210+0,053+0+0=0,263 (кг·м²);
I пр 8=336,7·(0,037)²+7,653·(0,068)²+2,251·(0,129)² + 102·(0,028)²=0,461+0,035+0,037+ +0,08=0,613 (кг·м²);
I пр 9=336,7·(0,045)²+7,653·(0,035)²+2,251·(0,197)² + 102·(0,042)²=0,682+0,01+0,087+ +0,18=0,959 (кг·м²);
I пр 10=336,7·(0,05)²+7,653·(0)²+2,251·(0,238)² + 102·(0,05)²=0,842+0+0,126+0,255=1,223 (кг·м²);
I пр 11=336,7·(0,046)²+7,653·(0,035)²+2,251·(0,21)² + 102·(0,043)²=0,712+0,01+0,099+ +0,189=1,01 (кг·м²);
I пр 12=336,7·(0,036)²+7,653·(0,062)²+2,251·(0,133)² + 102·(0,027)²=0,436+0,029+0,04+ +0,074=0,579 (кг·м²);
Значение первой производной приведённого момента инерции по углу поворота кривошипа определим, используя аппроксимацию первой производной конечными разностями:
I´ пр i=(dI пр i/dφi)=(I пр (i+1) -I пр i)/(φ(i+1) -φi), (10)
где I пр(i +1), I пр i – значения приведённого момента инерции для i+1 и i-го положений кривошипа, соответственно;
φ (i +1) и φi – значения угла поворотакривошипа для i+1 и i-го положений кривошипа, соответственно.
Для вычисления первой производной I ´пр(φ) по формуле (10) необходимо дополнительно разбить график I пр(φ) на интервалы, т.к. стандартных двенадцати положений явно недостаточно.
В положениях 8, 15, 22 функция I пр(φ) имеет экстремумы, поэтому первая производная I ´пр(φ) в этих точках равна нулю. Проведём расчёт I ´пр(φ) по формуле (10):
I ´пр1= 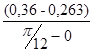 =
=  = 0,371 (кг·м²/рад);
= 0,371 (кг·м²/рад);
I ´пр2=  =
=  = 0,5 (кг·м²/рад);
= 0,5 (кг·м²/рад);
I ´пр3=  =
= 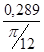 = 1,104 (кг·м²/рад);
= 1,104 (кг·м²/рад);
I ´пр4= 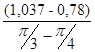 =
= 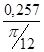 = 0,982 (кг·м²/рад);
= 0,982 (кг·м²/рад);
I ´пр5= 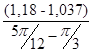 =
= 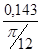 = 0,546 (кг·м²/рад);
= 0,546 (кг·м²/рад);
I ´пр6= 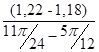 =
=  = 0,306 (кг·м²/рад);
= 0,306 (кг·м²/рад);
I ´пр7= 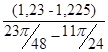 =
=  = 0,076 (кг·м²/рад);
= 0,076 (кг·м²/рад);
I ´пр8=  =
=  =- 0,076 (кг·м²/рад);
=- 0,076 (кг·м²/рад);
I ´пр9=  =
=  =- 0,458 (кг·м²/рад);
=- 0,458 (кг·м²/рад);
I ´пр10= 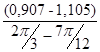 =
=  =- 0,756 (кг·м²/рад);
=- 0,756 (кг·м²/рад);
I ´пр11=  =
=  =- 0,867 (кг·м²/рад);
=- 0,867 (кг·м²/рад);
I ´пр12= 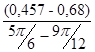 =
= 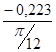 =- 0,852 (кг·м²/рад);
=- 0,852 (кг·м²/рад);
I ´пр13=  =
= 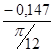 =- 0,562 (кг·м²/рад);
=- 0,562 (кг·м²/рад);
I ´пр14=  =
=  =- 0,31 (кг·м²/рад);
=- 0,31 (кг·м²/рад);
I ´пр15=  =
= 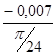 =- 0,054 (кг·м²/рад);
=- 0,054 (кг·м²/рад);
I ´пр16= 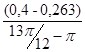 =
=  = 0,523 (кг·м²/рад);
= 0,523 (кг·м²/рад);
I ´пр17= 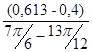 =
= 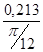 = 0,814 (кг·м²/рад);
= 0,814 (кг·м²/рад);
I ´пр18=  =
=  = 0,676 (кг·м²/рад);
= 0,676 (кг·м²/рад);
I ´пр19= 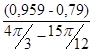 =
=  = 0,646 (кг·м²/рад);
= 0,646 (кг·м²/рад);
I ´пр20=  =
=  = 0,615 (кг·м²/рад);
= 0,615 (кг·м²/рад);
I ´пр21=  =
=  = 0,535 (кг·м²/рад);
= 0,535 (кг·м²/рад);
I ´пр22=  =
=  =- 0,008 (кг·м²/рад);
=- 0,008 (кг·м²/рад);
I ´пр23=  =
=  =- 0,241 (кг·м²/рад);
=- 0,241 (кг·м²/рад);
I ´пр24=  =
=  =- 0,573 (кг·м²/рад);
=- 0,573 (кг·м²/рад);
I ´пр25=  =
=  =- 0,802 (кг·м²/рад);
=- 0,802 (кг·м²/рад);
I ´пр26= 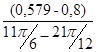 =
=  =- 0,844 (кг·м²/рад);
=- 0,844 (кг·м²/рад);
I ´пр27=  =
=  =- 0,646 (кг·м²/рад);
=- 0,646 (кг·м²/рад);
По результатам вычислений I ´пр(φ) строим график зависимости первой производной I пр от угла поворота кривошипа. Значения I ´пр(φ) в выбранных положениях (в таблицу занесены только основные положения) приведены в Таблице 4. Экстремумы функции в точках 8, 22 смещены в положения 4, 10, соответственно.
По формуле 6 рассчитаем момент движущих сил для преодоления сил динамического сопротивления во всех выбранных положениях механизма:
Мдин=107,3113·d I пр/ d φ;
Мдин1=107,3113·0=0 (н·м);
Мдин2=107,3113·0,5=53,656 (н·м);
Мдин3=107,3113·0,982=105,38 (н·м);
Мдин4=107,3113·(-0,08)=-8,585 (н·м);
Мдин5=107,3113·(-0,76)=-81,557 (н·м);
Мдин6=107,3113·(-0,85)=-91,215 (н·м);
Мдин7=107,3113·(-0,05)=-5,366 (н·м);
Мдин8=107,3113·0,814=87,351 (н·м);
Мдин9=107,3113·0,646=69,323 (н·м);
Мдин10=107,3113·(-0,01)=-1,073 (н·м);
Мдин11=107,3113·(-0,57)=-61,167 (н·м);
Мдин12=107,3113·(-0,84)=-90,142 (н·м).
Полученные значения Мдин приведены в Таблице 4.
График зависимости Мдин (φ) показан на Рисунке 13.

Рисунок 12. Зависимости приведённого момента инерции I пр и его первой производной I ´пр от угла поворота кривошипа.
РАСЧЁТ КПД МЕХАНИЗМА
Момент движущих сил Мдв, в соответствии с зависимостью (1), был определён в предположении, что кинематические пары механизма идеальны.
Влияние сил трения учитывают с помощью коэффициента полезного действия η. При последовательном соединении кинематических пар их общий КПД определяется следующим выражением:
η=η1·η2·……·ηк , где к -число кинематических пар.
При параллельном соединении кинематических пар КПД определяется как среднее арифметическое КПД отдельных пар, при условии, что поток мощности распределяется равномерно между кинематическими парами:
η=(η1+η2+…+ηк)/к, где к -число кинематических пар.
Суммарный КПД для нашего механизма (Рисунок 14) равен:
η∑= [(ηс+ηс)/2]·ηс·ηк·ηпн2·ηпн4·ηк·[(ηс+ηс)/2]= ηс·ηс·ηк·ηпн2·ηпн4·ηк·ηс=
= η3с· η2к·ηпн2·ηпн4 , (11)
где ηс= 0,98 – КПД подшипника скольжения;
ηк= 0,99 – КПД подшипника качения;
ηпн2 =0,86 – КПД кинематической пары «ползун по направляющей»;
ηпн4 =0,86 – КПД кинематической пары «пуансон по направляющей»;
Т.к. сила, определяющая в направляющих потери на трение, была учтена явным образом при подсчёте статического момента, то в формулу вычисления КПД она не входит.
η∑= (0,98)3·(0,99)2 · 0,86·0,86=0,68.
РАСЧЁТ ДВИЖУЩЕГО МОМЕНТА М∑(Φ)
По формуле (1) мы определяем момент движущих сил, считая, что кинематические пары идеальны. Однако силы трения присутствуют всегда, и их обычно учитывают с помощью коэффициента полезного действия – КПД.
Выражение для суммарного момента движущих сил М∑ с учётом потерь на трение примет вид:
М∑= k ·( Мст+Мдин ), (12)
где k – коэффициент, учитывающий присутствие сил трения в кинематических парах, равный: k =η, если (Мдв<0) – соответствуетработе привода в режиме генератора (когда привод играет роль тормоза);
k =1/η, если (Мдв>0) – соответствует работе привода в режиме двигателя.
Используя данные Таблицы 4, рассчитаем суммарный момент движущих сил М∑ для всех выбранных положений механизма:
М∑1=Мдв1/ η= 82,5/0,68=121,32 (н·м);
М∑2=Мдв2/ η= 115,2/0,68=169,41 (н·м);
М∑3=Мдв3/ η= 138,8/0,68=204,12 (н·м);
М∑4=Мдв4/ η= 78,91/0,68=116,04 (н·м);
М∑5=Мдв5/ η= 123,6/0,68=181,76 (н·м);
М∑6=Мдв6· η= -151·0,68=-102,68 (н·м);
М∑7=Мдв7· η= -87,9·0,68=-59,77 (н·м);
М∑8=Мдв8· η= -1,85·0,68=-1,26 (н·м);
М∑9=Мдв9/ η= 12,92/0,68=19 (н·м);
М∑10=Мдв10· η= -1,07·0,68=-0,73 (н·м);
М∑11=Мдв11· η= -13,3·0,68=-9,04 (н·м);
М∑12=Мдв12· η= -14,6·0,68=-9,93 (н·м);
М∑13=Мдв13/ η= 82,5/0,68=121,32 (н·м);
Полученные данные приведены в Таблице 4.
Зависимость М∑(φ) представлена на Рисунке 13.
Таблица 4. Результаты расчёта момента движущих сил и его составляющих.
| № положения | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 1 |
| φ, рад | 0 | π/6 | π/3 | π/2 | 2π/3 | 5π/6 | π | 7π/6 | 4π/3 | 3π/2 | 5π/3 | 11π/6 | 2π |
| Мст, н•м | 82,5 | 61,58 | 33,41 | 87,5 | 205,2 | -59,6 | -82,5 | -89,2 | -56,4 | 0 | 47,9 | 75,48 | 82,5 |
Q, кН
0
0
0
1,75
5,54
0
0
0
0
0
0
0
0
Iпр, кг•м²
0,263
0,491
1,037
1,225
0,907
0,457
0,263
0,613
0,959
1,223
1,01
0,579
0,263
I´пр, кг•м²/рад
0
0,5
0,982
-0,08
-0,76
-0,85
-0,05
0,814
0,646
-0,01
-0,57
-0,84
0
Мдин, н•м
0
53,66
105,4
-8,59
-81,6
-91,2
-5,37
87,35
69,32
-1,07
-61,2
-90,1
0
Мдв, н•м
82,5
115,2
138,8
78,91
123,6
-151
-87,9
-1,85
12,92
-1,07
-13,3
-14,6
82,5
М∑, н•м
121,3
169,4
204,1
116
181,8
-103
-59,8
-1,26
19
-0,73
-9,04
-9,93
121,3



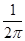 ·∫ М∑(φ) d φ, (14)
·∫ М∑(φ) d φ, (14)