 |
Эквивалентность и преобразование формул
|
|
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
 |
ФГБОУ ВО
“Воронежский государственный УНИВЕРСИТЕТ
ИНЖЕНЕРНЫХ технологиЙ”
Кафедра информационных технологий,
Моделирования и управления
 |
АЛГЕБРЫ ВЫСКАЗЫВАНИЙ И ПРЕДИКАТОВ
Методические указания
К практическим занятиям
Для студентов, обучающихся по направлению
09.03.02 – “Информационные системы и технологии”
Очной формы обучения
ВОРОНЕЖ
УДК 517.11(075.8)
Алгебры высказываний и предикатов [Электронный ресурс]: метод. указания к практическим занятиям / Воронеж. гос. ун-т инж. технол.; сост. Ю. В. Бугаев, И. Ю. Шурупова. – Воронеж: ВГУИТ, 2015. – 28 с. – [ЭИ]
Методические указания разработаны в соответствии с требованиями ФГОС ВО подготовки выпускников по направлениям 09.03.02 – “Инфор-мационные системы и технологии”. Они предназначены для закрепления теоретических знаний дисциплины по выбору “Математическая логика и теория алгоритмов” вариативной части блока Б1. Работа содержит методику выполнения практических заданий и варианты заданий для самостоятельной работы.
Библиогр.: 6 назв.
Составители: профессор Ю.В. БУГАЕВ,
доцент И.Ю. ШУРУПОВА
Научный редактор доцент Л.А. КОРОБОВА
Рекомендуется к размещению
в ЭОС и ЭБ ВГУИТ
Ó Бугаев Ю.В., Шурупова И.Ю.
Ó ФГБОУ ВПО “Воронежский
государственный университет
инженерных технологий”, 2015
Оригинал-макет данного издания является собственностью Воронежского государственного университета инженерных технологий, его репродуцирование (воспроизведение) любым способом без согласия университета запрещается.
|
|
|
Цель занятий - овладение основными понятиями и методами алгебры высказываний и логики предикатов, выработка навыков решения практических задач.
Процесс изучения дисциплины направлен на формирование компетенции:
- способность использовать основные законы естественнонаучных дисциплин в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования (ОПК-2).
Формулы алгебры высказываний.
Эквивалентность и преобразование формул
Напомним определение формулы алгебры высказываний. Формулами алгебры высказываний являются:
1) логические константы 0 и 1;
2) пропозициональные переменные;
3) если U и V – формулы, то каждое из выражений Ø(U), (U) Ù (V), (U) Ú (V), (U) ® (V), (U) ~ (V) есть формула;
4) других формул, построенных не по пп. 1) - 3), нет.
Для проверки свойств эквивалентности, выполнимости, опровержимости, тождественной истинности и ложности формул могут использоваться таблицы истинности. Для построения таблицы истинности формулы воспользуемся следующим алгоритмом.
1. Пронумеровать простые высказывания в алфавитном порядке.
2. Для каждого элементарного высказывания рассмотреть все возможные наборы значений истинности. Всего возможно 2n комбинаций, где n - число элементарных высказываний. Это количество строк в таблице.
3. Пронумеровать сложные высказывания, содержащие одну логическую операцию, затем сложные высказывания, содержащие две логических операции, и т.д., увеличивая сложность высказываний в соответствии с порядком выполнения операций.
4. Вычислить значения истинности всех сложных высказываний. Столбец с последним номером будет содержать значение истинности для всей логической формулы.
Задание 1.1. Построить таблицу истинности формулы
Ø(А Ù В) ® ØА Ú С.
|
|
|
Решение.
1. Пронумеруем простые высказывания в алфавитном порядке А-1, В-2, С-3.
2. Каждый набор значений истинности элементарных высказываний изобразится набором 000, 001, 010 и т. д. Для нашего примера число комбинаций равно 8-ми, то есть таблица истинности будет содержать 8 строк.
3. Пронумеруем сложные высказывания формулы: АÙВ - 4; Ø(AÙB) - 5; ØA - 6; ØAÚС - 7; конечная операция ® - 8.
4. Вычислим последовательно значения истинности сложных высказываний.
| Ø (A Ù B) | ® | Ø A Ú С | ||||||
Анализируя истинностные значения формулы, содержащиеся в столбце 8, получим, что данная формула является и выполнимой, и опровержимой, и, следовательно, не тавтология и не противоречие. Для проверки эквивалентности формул строятся их таблицы истинности на одинаковых интерпретациях.
Однако такой способ очень громоздок, поэтому в дальнейшем решать такие задачи будем с помощью эквивалентных преобразований, используя основные тавтологии 1-13 (см. лекции или учебное пособие).
Задание 1.2. Доказать эквивалентность формул
 .
.
Решение.
 º
º 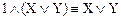
Двойственная формула  доказывается аналогично. В дальнейшем при проведении преобразований формул эти законы, называемые законами обобщенного склеивания, будут часто использоваться, поэтому добавим их под номером 14 в список основных тавтологий.
доказывается аналогично. В дальнейшем при проведении преобразований формул эти законы, называемые законами обобщенного склеивания, будут часто использоваться, поэтому добавим их под номером 14 в список основных тавтологий.
Задание 1.3. Доказать эквивалентность формул
(AÚ B) Ù (B Ú C) Ù (C Ú A) º (A Ù B) Ú (B Ù C) Ú (C Ù A).
Решение.
(AÚ B) Ù (B Ú C) Ù (C Ú A) º (BÚ (A Ù C)) Ù (C Ú A) º
º (B Ù (C Ú A)) Ú (A Ù C Ù (C Ú A)) º (B Ù C) Ú (B Ù A) Ú (A Ù C).
Как легко видеть, последняя формула цепочки эквивалентна формуле правой части задания в силу коммутативности операций Ù и Ú. Данные формулы являются самодвойственными.
Для того чтобы воспользоваться тавтологиями 1-14 требуется привести формулу к приведенному виду. Определим порядок построения приведенной формулы.
1. Удаляются операции импликация и эквиваленция по формулам 11, 12.
2. Операции отрицания спускаются до высказывательных переменных с помощью законов де Моргана и двойного отрицания.
В дальнейшем, если это возможно, полученная приведенная формула упрощается с помощью свойств 3, 4, 5, 6, 9, 10.
|
|
|
Задание 1.4. Доказать тождественную истинность формулы
(P ® R) ® ((Q ® R) ® ((P Ú Q) ® R)).
Решение.
(P ® R) ® ((Q ® R) ® ((P Ú Q) ® R)) º
º Ø( ) Ú (Ø(
) Ú (Ø( ) Ú (Ø(P Ú Q) Ú R) º
) Ú (Ø(P Ú Q) Ú R) º
º (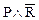 ) Ú (
) Ú ( ) Ú (
) Ú ( ) Ú R º R Ú P Ú (
) Ú R º R Ú P Ú ( ) Ú (
) Ú ( ) º º R Ú P Ú Q Ú (
) º º R Ú P Ú Q Ú ( ) º R Ú P Ú Q Ú
) º R Ú P Ú Q Ú  º R Ú Q Ú 1 º 1.
º R Ú Q Ú 1 º 1.
Начиная с 3-й, все формулы цепочки преобразований являются приведёнными.
Задание 1.5. Упростить схему

Решение. Запишем формулу, соответствующую схеме, по приведенным выше правилам
U = 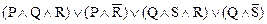 .
.
|
|
|


