 |
Формулы алгебры предикатов сигнатуры s
|
|
|
|
Напомним, что строго предикат можно определить как отображение n -ной степени предметного множества M, называемой местностью или арностью предиката в двухэлементное множество B = {1, 0}
.
Например, предикат простого числа 
задаётся правилом 
и может быть определён на произвольном числовом множестве. Всюду в дальнейшем для краткости будем определять предикаты записью 
.
Для предикатов кроме логических операций алгебры высказываний вводятся операции утверждения общности и утверждения существования, называемые операциями связывания предметных переменных. С помощью этих операций из предикатов строятся формулы алгебры предикатов.
Например, для предиката делимости D(x,y): ² x нацело делится на y ², определённого на множестве натуральных чисел N, можно построить формулы алгебры предикатов, являющиеся высказываниями, так как обе предметные переменные в них связаны.
1) Высказывание 
читается, как “для любого x существует y, такое, что x делится на y ”, и является истинным высказыванием, так как любое натуральное x делится на себя и на 1, т.е. y = x или y =1;
2) Высказывание 
читается, как “существует y, на который делится любой x ”, и является истинным высказыванием, так как на значение y =1 делится любое натуральное x;
3) Высказывание 
читается, как “существует x, который делится на любое y ”, и является ложным высказыванием, так как нет ни одного натурального числа, которое делится на любое натуральное число;
4) Высказывание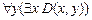 
читается, как “для любого y существует такой x, что x делится на y ”, и является истинным высказыванием, так как для любого натурального y можно указать множество значений 
N, которые делятся на y.
Ряд важнейших понятий алгебры предикатов основывается на понятии модели.
|
|
|
Моделью M называется любое множество M с заданными на нем предикатами 
:
M = < M; >,
а набор s = < 
> называется сигнатурой модели M.
Любое утверждение в некоторой предметной области можно записать в виде формулы алгебры предикатов сигнатуры s, выбрав соответствующее предметное множество и набор предикатов, определённых на нём, называемый сигнатурой модели. В качестве примера рассмотрим теоремы и определения из евклидовой геометрии. Предметным множеством M здесь является множество точек, прямых и плоскостей трёхмерного пространства.
Задание 5.1. Записать в виде формулы на модели
M g= < M;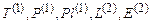 
>, где
, 
,
, 
,
,
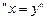следующие утверждения:
a) Через каждые 2 точки можно провести прямую.
b) Если 2 точки различны, то проходящая через них прямая единственна.
c) Через каждые 3 точки, не лежащие на одной прямой, можно провести единственную плоскость.
d) Определение параллельных прямых на плоскости.
Решение.
a) Данное утверждение можно сформулировать с использованием предикатов модели следующим образом: для произвольных двух точек существует прямая, на которой лежат эти точки. Запишем его в виде формулы
b) В дополнении к предыдущему утверждению здесь говорится, что если произвольные точки не совпадают, то построенная по ним прямая является единственной, т.е. любая другая прямая, проходящая через эти точки, совпадает с ней. Таким образом, получим формулу
c) Данное утверждение гласит, что если 3 точки не лежат на одной прямой, то существует плоскость, на которой лежат эти точки, причём любая другая такая плоскость совпадает с ней. Введём для краткости записи итоговой формулы вспомогательные формульные предикаты:
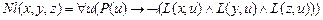: “ x, y, z не лежат на одной прямой“;
: “ x, y, z лежат на плоскости v “.
Запишем с их помощью утверждение задания
.
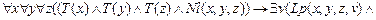
d) Напомним, что параллельными называются те прямые, которые лежат на одной плоскости и не имеют общих точек, либо совпадают, т.е.
|
|
|
.
Заметим, что в предыдущих формулах все переменные – связанные, т.е. формулы являются высказываниями, принимающими значение 1. Данная формула является формульным предикатом от переменных 
, который может принимать различные значения для конкретных значений переменных.
Контрольные вопросы и задания
1. Представить формулой на модели
M P = < P; M(1), W(1), C(2), Y(2), G(2)>, где
M(x): ² x – мужчина²,
W(x): ² x – женщина²,
C(x, y): ² x ребёнок y ²,
Y(x, y): ² x моложе, чем y ²,
G(x, y): ² x состоит в браке с y ²,
следующие утверждения:
a) Каждый человек имеет отца и мать.
b) Каждый, кто имеет отца, имеет и мать.
c) Каждый человек моложе своих родителей.
d) Каждый человек моложе родителей своих родителей.
e) Человек x состоит в браке.
f) x и y братья (т.е. имеют общих родителей).
g) Все дети человека x состоят в браке.
h) Каждый ребёнок человека y состоит в браке с ребёнком человека x.
2. В модели с одним двуместным предикатом 
записать утверждения:
a) предикат R рефлексивен;
b) предикат R симметричен;
c) предикат R транзитивен;
d) предикат R является отношением эквивалентности.
3. Определить являются ли следующие формулы на модели M 1 = < N; D (2), S (3), P (3)>, где D(x,y): “ x нацело делится на y ”, 
выполнимыми, истинными, ложными на модели?
a) 
b)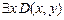 
c) 
d)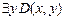 
e) 
f) 
4. Построить на модели M 2 = < N; S (3), P (3)> формулу, принимающую значение истина тогда и только тогда, когда:
a) x = 0;
b) x = 1;
c) x = 2;
d) x – чётно;
e) x – нечётно;
f) x – простое число.
|
|
|
