 |
Формулы алгебры предикатов
|
|
|
|
Математическая логика описывает общие методы умозаключений, применяемые к утверждениям, записанным в виде формул. Поэтому от символов предикатов фиксированной сигнатуры в формулах алгебры предикатов сигнатуры s перейдём к предикатным переменным. Например, формула
U = 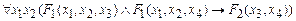 (1)
(1)
является формулой алгебры предикатов, в которой  - произвольные предикаты арности 3 и 2 соответственно. Для определения же свойств таких формул рассматриваются формулы сигнатуры s, полученные замещением предикатных переменных на предикаты некоторой заданной сигнатуры s.
- произвольные предикаты арности 3 и 2 соответственно. Для определения же свойств таких формул рассматриваются формулы сигнатуры s, полученные замещением предикатных переменных на предикаты некоторой заданной сигнатуры s.
Задание 6.1. Является ли модель арифметики натуральных чисел M a = < N; E (2), S (3), P (3)>, где



допустимой для формулы (1)? Определить является ли формула (1) выполнимой на модели M a, просто выполнимой, тождественно истинной на модели M a, общезначимой?
Решение. Модель арифметики натуральных чисел является допустимой для формулы U, так как можно построить сигнатурное отображение  множества предикатных переменных формулы
множества предикатных переменных формулы  в сигнатуру модели s = < E (2), S (3), P (3)>. Вариантов такого отображения два:
в сигнатуру модели s = < E (2), S (3), P (3)>. Вариантов такого отображения два:
1)  ,
,  ;
;
2)  ,
,  .
.
Проверим, является ли формула выполнимой на допустимой модели N. Рассмотрим формулу
s1 U =  ,
,
полученную подстановкой в формулу U предикатов сигнатурного отображения å1. Легко проверить, что s1 U  = 1 для любых значений
= 1 для любых значений  , так как
, так как
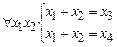 Þ
Þ  , является истинным утверждением.
, является истинным утверждением.
Это означает, что формула U выполнима на модели M a и, более того, она истинна на этой модели. Выполнимость формулы следует из её выполнимости на модели M a.
Для проверки тождественной истинности формулы на модели нужно проверить истинность s U при любом сигнатурном отображении. Аналогично предыдущему случаю получим, что формула s2 U =  истинна на модели M a, а следовательно U тождественно истиннана этой модели.
истинна на модели M a, а следовательно U тождественно истиннана этой модели.
|
|
|
Данная формула не является общезначимой, чтобы доказать это достаточно привести пример допустимой модели, на которой формула не будет тождественно истинной. В качестве такой модели возьмем M 3 = < N; G (2), S (3), P (3)>, где  .
.
Для доказательства общезначимости формулы нужно показать её тождественную истинность на любой допустимой модели, т. е. для любого предметного множества и любых предикатов соответствующей арности.
Задание 6.2. Доказать общезначимость формулы
 .
.
Решение. Так как единственная переменная в обеих частях эквиваленции связана, то обе они являются высказываниями. Поэтому для доказательства общезначимости формулы, покажем, что истинностные значения левой и правой части совпадают для любых одноместных предикатов 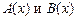 , определённых на произвольном множестве M.
, определённых на произвольном множестве M.
Пусть  , тогда по определению операции утверждения общности
, тогда по определению операции утверждения общности  M, откуда следует, что
M, откуда следует, что 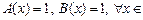 M, это означает, что
M, это означает, что  и
и  , а, следовательно, истинна и их конъюнкция
, а, следовательно, истинна и их конъюнкция  . Те же рассуждения справедливы и в обратную сторону.
. Те же рассуждения справедливы и в обратную сторону.
Задание 6.3. Построить ПН-форму для формулы

Решение. Воспользовавшись общезначимостью из предыдущего задания, получим
 º
º
º  .
.
В первом дизъюнкте переменные x и y – связанные, а z – свободная, а во втором – наоборот. Переобозначив связанные переменные  º
º
º  ,
,
получим, что первый дизъюнкт не зависит от w, а второй – от u и v. Поэтому, вынеся соответствующие им кванторы в начало формулы  º
º
º  получим её ПН-форму.
получим её ПН-форму.
Контрольные вопросы и задания
1. Является ли модель M = < M; T(0), Q(1), R(1), P(2), S(2)> допустимой для формул:
a)  ;
;
b) 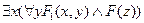 .
.
Определить является ли формула выполнимой на модели, просто выполнимой, тождественно истинной на модели, общезначимой, если M ={ a, b }, T(0) = 1, а остальные предикаты заданы таблицами?
| x | Q | R |
| a b |
| x | y | P | S |
| a a b b | a b a b |
2. Является ли модель арифметики натуральных чисел допустимой для формул. Определить является ли формула выполнимой на модели, просто выполнимой, ложной на модели, невыполнимой, тождественно истинной на модели, общезначимой?
|
|
|
a) 
b) 
3. Доказать общезначимость формул:
a) 
b) 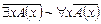
c) 
d) 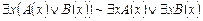
e) 
f) 
4. Выполнимы ли следующие формулы:
a) 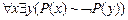 ;
;
b)  ;
;
c)  ;
;
d)  .
.
5. Построить ПН-форму для формул:
a)  ;
;
b)  ;
;
c)  ;
;
d)  .
.
6. Привести формулу к клазуальной нормальной форме:
a)  ;
;
b)  ;
;
c) 
 ;
;
d)  ;
;
e) 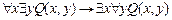 ;
;
f)  .
.
Библиографический список
Основной
1. Судоплатов, С. В. Математическая логика и теория алгоритмов [Текст]: учебник для студ. вузов (гриф МО) / С. В. Судоплатов, Е. В. Овчинникова. - М.; Новосибирск: ИНФРА - М; НГТУ, 2004. - 224 с.
2. Новиков, Ф. А. Дискретная математика для программистов [Текст]: учебное пособие для студ. вузов (гриф МО) / Ф. А. Новиков. - 2-е изд. - СПб.: ПИТЕР, 2006. - 364 с.
3. Лавров, И.А. Задачи по теории множеств, математической логике и теории алгоритмов [Текст] / И.А. Лавров, Л.Л. Максимова - М.: Физматлит, 2002. - 256 с.
4. Верещагин, Н.К. Вводный курс математической логики: учебное пособие / Н.К. Верещагин, В.А. Успенский, В.Е Плиско. – ФИЗМАТЛИТ, 2007. – 126 с. (http://www.iprbookshop.ru)
Дополнительный
5. Кузнецов, О.П. Дискретная математика для инженеров [Текст]: учебник для вузов (гриф Пр. / О.П. Кузнецов - 5-е изд., стер. - СПб.: Лань, 2007. - 400 с.
6. Эдельман, С.Л. Математическая логика [Текст]: учебное пособие для ин-тов / С.Л. Эдельман - М.: Высш. школа, 1975. - 176 с. с ил.
Электронное издание
|
|
|


