 |
Алгоритм имитационной модели одноканальной СМО
|
|
|
|
Министерство образования Российской Федерации
Государственное образовательное учреждение высшего профессионального образования
Таганрогский государственный радиотехнический университет
В.И.ФИНАЕВ
АЛГОРИТМИЗАЦИЯ И ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ
С ПРИМЕНЕНИЕМ
АППАРАТА СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ
Таганрог 2003
УДК 62 – 501.72:519.52(07.07)
В.И. Финаев В.И. Алгоритмизация и имитационное моделирование с применением аппарата систем массового обслуживания: Учебное пособие. Таганрог: ТРТУ, 2003. 72 с.
Рассматриваются особенности построения алгоритмов для имитационного моделирования процессов функционирования искусственных систем различного назначения (производственных, экономических, систем связи, коммунального обслуживания и прочее). При алгоритмизации функционирование интерпретируется, как функционирование системы массового обслуживания. Результаты функционирования в имитационной модели фиксируются в подпрограммах набора данных для последующей статистической обработки и построения кумулятивных эмпирических функций распределения вероятностей рассматриваемых событий.
Табл. 2. Ил. 67. Библиогр.: 7 назв.
Печатается по решению редакционно-издательского совета Таганрогского государственного радиотехнического университета.
Рецензенты:
Региональный (областной) центр новых информационных технологий, директор центра, д.т.н., профессор В.М.Курейчик;
А.В. Маргелов, д. т. н., профессор, ведущий научный сотрудник ТНИИС.
Ó Таганрогский государственный
радиотехнический университет, 2003
ОГЛАВЛЕНИЕ
|
|
|
ВВЕДЕНИЕ 4
1. ИМИТАЦИОННАЯ МОДЕЛЬ ОДНОКАНАЛЬНОЙ СМО 9
1.1. Алгоритм имитационной модели одноканальной СМО 9
1.2. Алгоритмы подпрограмм 14
ПОСТРОЕНИЕ ИМИТАЦИОННОЙ МОДЕЛИ ПРИ
ПРОИЗВОЛЬНОМ РАСПРЕДЕЛЕНИИ ВХОДНОГО ПОТОКА 26
3. ИМИТАЦИОННЫЕ МОДЕЛИ МНОГОФАЗНЫХ СМО 30
4. ИМИТАЦИОННЫЕ МОДЕЛИ МНОГОКАНАЛЬНЫХ СМО 35
2.1 Модели систем с общей очередью 35
4.2 Модели СМО с очередью к каждому прибору 45
ИМИТАЦИОННЫЕ МОДЕЛИ СМО
С ОТНОСИТЕЛЬНЫМИ ПРИОРИТЕТАМИ 52
6. АЛГОРИТМИЗАЦИЯ ИМИТАЦИОННОЙ МОДЕЛИ СМО ПРОИЗВОЛЬНОЙ СТРУКТУРЫ 55
7. ВАРИАНТЫ ЗАДАНИЙ 60
8. ВОПРОСЫ И ОТВЕТЫ ДЛЯ САМОПРОВЕРКИ 68
БИБЛИОГРАФИЧЕСКИЙ СПИСОК 71
ВВЕДЕНИЕ
Существует развитый математический аппарат, описывающий функционирование систем массового обслуживания (СМО).
СМО состоит из входного потока заявок (одного или нескольких), прибора или приборов обслуживания, выходного потока заявок, обслуженных или покинувших систему, не дождавшись окончания обслуживания.
Исходя из характеристик потоков заявок и структуры приборов обслуживания [1-6], СМО классифицируют следующим образом.
По потокам заявок СМО делятся на СМО с однородным потоком и приоритетные СМО.
Исходя из того, каким временем на ожидание располагает заявка, СМО делятся на СМО с отказами, если эта величина времени ожидания равна нулю, смешанные СМО, если время ожидания является конечной величиной (СМО с ограниченной очередью), СМО с ожиданием, если время ожидания является бесконечной величиной (с бесконечной очередью).
По количеству и структурному расположению приборов обслуживания СМО делятся на одноканальные (рис.В.1,а), n -канальные, если имеются n параллельно расположенных приборов (рис.В.1,б), m -фазные СМО, если имеются последовательно расположенные m приборов (рис.В.1,в), СМО смешанной структуры (рис.В.1,г).
Классификация может быть осуществлена, исходя из математических законов, описывающих математические модели входного потока заявок и времени обслуживания.
|
|
|
Таким образом, при моделировании объекта с применением математического языка СМО требует выделения в процессе формализации понятий: заявка (требование), поток заявок, прибор обслуживания, очередь на обслуживание, дисциплины выбора на обслуживание, закон обслуживания, поток обслуженных заявок, поток потерянных заявок.
Моделирование сложных систем с применением схем СМО требует формального определения входных и выходных параметров, параметров состояния, на основе которых определяются показатели эффективности функционирования системы.
Основной моделью, описывающей функционирование такой системы, как СМО, является описание времени задержки в системе. В качестве показателей эффективности могут быть применены:
- коэффициент использования системы как отношение интенсивности поступающих на обслуживание заявок к интенсивности их обслуживания;
- вероятность того, что поступившая в СМО заявка застанет ее свободной от обслуживания;
- описание периода занятости системы, т.е. интервалов времени, в течение которых прибор «работает» не прерываясь;
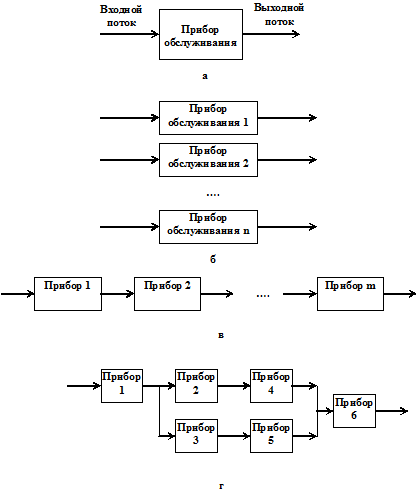
Рис.В.1
- вероятность отказа на обслуживание;
- среднее число заявок в очереди;
- описание выходных потоков заявок,
- другие интегральные показатели функционирования СМО.
Почему аппарат теории массового обслуживания широко применим при моделировании систем самого различного назначения?
Если это системы, связанные с обслуживанием клиентов, например в прачечной, химчистке, кассе и прочее, то здесь очевидно применение аппарата. Моделями СМО адекватно моделируются процессы погрузки транспорта, стрельба по целям, передача информации по каналам связи, потоки транспортных средств, перевозка грузов, обработка деталей на станке и многие другие процессы функционирования разных систем.
Изготовление какого-либо изделия, состоящего из большого числа деталей, можно представить в виде модели СМО сложной структуры. Действительно, изготовление детали требует выполнение определенного множества последовательных операций на разных станках и, возможно, на разных производственных участках, например, отливка, штамповка, а затем токарные операции. Все эти операции, выполняемые на разных станках разными рабочими, в результате позволяют представить структуру сложной СМО. Однако здесь при моделировании появляются математические сложности.
|
|
|
Математическую модель СМО в виде системы уравнений Эрланга [1,2,3], как наиболее простую аналитическую модель, можно получить при пуассоновском потоке заявок и экспоненциальном распределении времени обслуживания. Удобство пользования данной моделью ограничивается требованием стационарности процессов и отсутствием необходимости оценки изменения вероятностных характеристик во времени.
Если же перед исследователем ставится более сложная задача оценки таких критериев, как функции распределения вероятностей времени задержки, периода занятости, числа заявок в очереди, то в этом случае можно применить математические модели, исследованные в работах [1,3,4,5].
Наиболее широко применяется описание математических моделей в виде характеристических функций, в частности, в виде преобразований Лапласа-Стильтьеса [4].
Модель времени задержки представима в виде интегро-дифференциального уравнения Линди-Такача-Севастьянова [1], причем в данной модели предполагается произвольный вид распределения времени обслуживания.
Однако при всей универсальности аппарата характеристических функций для применения его при описании моделей СМО, у него имеется один существенный недостаток, заключающийся в том, что получить реальные распределения действительного параметра времени далеко не всегда возможно. Это связано с тем, что не всегда существуют обратные преобразования Лапласа.
При моделировании приоритетных СМО применяют математические модели, изложенные в работах [4,6].
Если же рассматривать сложные структуры СМО (многофазные, многоканальные, приоритетные), то получить математическую модель в виде аналитических зависимостей невозможно. Поэтому для исследования сложных структур СМО разрабатывают имитационные модели.
|
|
|
При разработке имитационной модели некоторой исследуемой системы важно адекватно определить структуру СМО. Это сложная задача, требующая детального изучения реальных процессов функционирования систем.
После того, как структура получена, т.е. выделены приборы обслуживания, определены входные потоки и потоки между приборами, можно приступить к алгоритмизации.
Алгоритмизация может осуществляться с применением способа Dt -моделирования. Этот способ позволяет определить последовательные состояния сложной системы через интервал времени Dt.
При применении способа Dt -моделирования процесс функционирования сложной системы рассматривают как последовательную смену состояний, заданных параметрами z1(t), z2(t),..., zn(t) в n -мерном фазовом пространстве.
Можно при алгоритмизации применить способ особых точек. При применении этого способа выделяют два типа состояний: обычные состояния, в который сиcтема находится почти вcе время; особые состояния, характерные для cиcтемы в некоторые изолированные моменты времени, совпадающие c моментами поступления в cиcтему входных сигналов от внешней cpеды, выхода параметра zi(t) на границу области существования и т.д. Координаты zi(t) в эти моменты времени могут изменяться cкачком.
Можно применить способ последовательной проводки заявок. При применении данного способа моделирующий алгоритм состоит в последовательном воспроизведении истории отдельных заявок в порядке поступления их в систему. Алгоритм обращается к сведениям о других заявках лишь в том случае, если это необходимо для решения задачи о дальнейшем порядке обслуживания данной заявки. Операторы моделирования составляют сложную логическую структуру.
В данном учебном пособии рассматриваются рекомендации по составлению имитационных моделей СМО сложных структур с применением способа Dt -моделирования.
В первом разделе учебного пособия приведен алгоритм имитационной модели одноканальной СМО при пуассоновском распределении входного потока заявок. Поступление заявки имитируется исходя из вероятности появления заявки за время Dt, а время обслуживания – из функции распределения вероятности длительности обслуживания. Алгоритм состоит из подпрограмм, последовательно связанных друг с другом исходя из логики функционирования СМО. Приведены алгоритмы подпрограмм имитационной модели.
Во втором разделе рассмотрены особенности алгоритма имитационной модели одноканальной СМО при произвольном распределении входного потока заявок. Поступление заявки имитируется исходя из задания модели входного потока. В разделе рассмотрено моделирование при задании модели входного потока в виде распределений вероятностей появления заданного числа заявок.
|
|
|
Рассмотрены изменения в алгоритме моделирования СМО и особенности построения подпрограмм набора статистических данных потока заявок и потока теряемых заявок, а также постановки заявок в очередь.
В третьем разделе учебного пособия рассмотрены особенности алгоритмизации многофазной СМО, состоящей из однотипных по параметрам систем.
В четвертом разделе изложен подход к алгоритмизации многоканальных СМО. Рассмотрена задача алгоритмизации имитационной модели трехканальной СМО с общей очередью, а также при постановке заявок в очередь к каждому из трех приборов. Модульный принцип построения алгоритма позволяет рассматривать любое число приборов обслуживания в структуре многоканальной СМО.
В пятом разделе рассмотрена алгоритмизация СМО с относительными приоритетами при бесконечной очереди.
В шестом разделе рассмотрен пример разработки алгоритма для СМО произвольной структуры. Приведены рекомендации по разработке алгоритмов СМО произвольных структур.
Седьмой раздел содержит варианты заданий для разработки алгоритмов и написания программных приложений для решения задач моделирования.
В конце пособия приведены вопросы и ответы, определяющие основные понятия СМО.
ИМИТАЦИОННАЯ МОДЕЛЬ
ОДНОКАНАЛЬНОЙ СМО
Алгоритм имитационной модели одноканальной СМО
Одноканальная СМО самая простая модель (см. рис.В.1,а) при условии пуассоновского входного потока заявок и экспоненциального (показательного) распределения времени обслуживания. Для такой СМО существуют аналитические модели.
Одноканальную СМО следует рассматривать как элемент, т.е. предел членения СМО сложной структуры. Поэтому алгоритмизацию начнем рассматривать вначале для одноканальной СМО.
Рассмотрим задачу построения имитационной модель одноканальной СМО с пуассоновским потоком заявок, характеризующимся интенсивностью a и функцией распределения времени обслуживания B(t).
Для СМО приняты обозначения А/В/m/L, в которых:
- первая позиция А определяет функцию распределения входного потока заявок (интервала времени между поступающими заявками);
- вторая позиция В определяет функцию распределения закона обслуживания;
- третья позиция определяет m число каналов (приборов) обслуживания;
- четвертая позиция L определяет максимально допустимое число заявок в очереди на обслуживание.
Аналитические законы функций распределений имеют следующее общепризнанное кодированное обозначение:
- М – показательное распределение;
- Er - распределение Эрланга r –го порядка;
- Hk - гиперпоказательное распределение порядка k;
- D - вырожденное распределение;
- G - произвольное распределение.
Если поток заявок пуассоновский, то СМО определена шифром M/G/1/PM.
Пусть максимально возможная длина очереди определится значением идентификатора JPM. Алгоритм имитационной модели разрабатываем по способу Dt -моделирования, т.е будем рассматривать изменение характеристик СМО за каждый, достаточно малый отрезок времени Dt.
Для понимания процесса функционирования одноканальной СМО следует построить временные диаграммы, на которых отображают время задержки w(t) заявок, а также определяют интервалы периода занятости p(t).
На рис.1.1 приведены временные диаграммы, отображающие процесс функционирования СМО.

Рис.1.1
Поток заявок П(t) описывается стохастическим распределением вероятностей длин интервалов между соседними заявками (показаны точками) либо вероятностями появления определенного числа заявок за время t.
Время задержки в момент поступления заявки скачком увеличивается на величину, равную времени обслуживания поступившей заявки, а затем убывает с угловым коэффициентом равным единице.
Интервалы периода занятости p(t) на нижней оси показаны выделенными отрезками (толстые линии). На рис.1.1 имеются идентификаторы М, о назначении которых будет сказано ниже.
При пуассоновском потоке заявок длины интервалов времени между соседними заявками описываются экспоненциальным распределением
A(t)=1-e-at.
Введем идентификаторы:
- I=1, если за такт моделирования Т=Δt поступила заявка с вероятностью Рn;
- I=0, если заявка в систему не поступила;
- М=1, если в СМО есть очередь на обслуживание;
- М=0, если очередь отсутствует;
- L=1, если прибор занят обслуживанием (в СМО одна и более заявок);
- L=0, если прибор от обслуживания свободен (в СМО нет заявок);
- К=1, если обслуживание окончено и заявка покидает СМО.
Тогда, применяя модульный принцип построения программы для имитационного моделирования, построим структурную схему алгоритма имитационной модели СМО M/G/I/JPM, вид которой приведен на рис.1.2.

Рис.1.2
Алгоритм имитационной модели построен в соответствии с процедурами поступления заявок в систему, постановки их в очередь при занятом приборе, обслуживания заявок.
Структура алгоритма имитационной модели состоит из подпрограмм, имитирующих конкретные операции в СМО. «Движение» по подпрограммам осуществляется с помощью ключей.
Работает алгоритм имитационной модели следующим образом.
Вначале происходит обращение к подпрограмме WWOD – ввод исходных данных, в которой описываются необходимые массивы, общие области, задаются начальные значения.
В начальный такт моделирования необходимо определить:
- счетчик тактов моделирования Т=0;
- идентификаторы М=0, L=0, так как нет очереди и прибор свободен от обслуживания;
- длительность времени обслуживания ВТ=0, так как в СМО нет заявок;
- число заявок в очереди JP=0;
- момент времени начала интервала до следующей заявки ТН=0;
- длительность периода занятости PZ=0;
- память под все массивы: N[J] – массив времен поступления J -х заявок в очередь; массивы чисел для сравнения получаемых случайных величин (интервалов времени между соседними заявками, времени ожидания очереди, числа потерянных заявок, времени обслуживания, периода занятости и т.д.) с их оценками;
- и ввести значение вероятности РР=Рn;
- заданное число тактов моделирования TZ, значение JPМ и т.д.
Затем наращивается такт моделирования (см. блок 2 на рис.1.2) и за данный отрезок времени Δt=1 просматриваются изменения в СМО, для чего и предусмотрены подпрограммы.
Далее по алгоритму следует обращение к подпрограмме GEN – генерация заявок входного потока (см. блок 3 на рис.1.2). Алгоритм подпрограммы GEN будет рассмотрен ниже. В подпрограмме GEN на основе анализа полной группы событий – поступления и непоступления заявок за рассматриваемый такт Т определяется факт появления заявки (идентификатор I=1) либо непоявления заявки (идентификатор I=0).
Зная такт моделирования Т, результат работы подпрограммы GEN, при I=1 (см. блок 4 на рис.1.2) и числе заявок в очереди, меньшем максимально возможного (см. блок 5 на рис.1.2), обращаемся к подпрограмме набора статистических данных потока заявок STATP. Это происходит потому, что заявка будет поставлена в очередь на обслуживание. Переход к подпрограмме STATP возможен также и в том случае, если в данном такте моделирования Т заявка поступила в СМО и в этом же такте СМО покидает заявка, обслуживание которой завершено, т.е. идентификатор L=0 (см. блок 6 на рис.1.2).
В подпрограмме STATP набираются статистические данные для построения эмпирической кумулятивной функции распределения А*(t) длин интервалов между двумя любыми соседними заявками. Алгоритм подпрограммы STATP будет рассмотрен ниже.
Затем следует постановка поступившей заявки в очередь, что осуществляется в подпрограмме OSTH. Анализ очереди на обслуживание состоит из анализа следующих событий:
а1) есть очередь и за такт Т поступила заявка;
а2) есть очередь и за такт Т не поступила заявка;
а3) нет очереди и за такт Т поступила заявка;
а4) нет очереди и за такт Т не поступила заявка.
Если поступившую в такт Т заявку идентифицировать обозначением N[J]=T, где J – ее номер в очереди, а N[J]=T – такт поступления заявки в систему, то при событии а1 поступившая заявка получит значение идентификатора N[J]=T, где J=JP+1, JP – число заявок в очереди в предшествующем такте Т-1. При событии а3 поступившая заявка получит значение идентификатора N[1]=T.
Если заявка поступила, а число заявок в очереди равно JPM, а также при полностью заполненном буфере очереди в этом такте не окончено обслуживание заявки, то поступившая заявка теряется. В этом случае происходит переход к подпрограмме набора статистических данных потерянных заявок STAТT.
Если прибор свободен от обслуживания (L=0) и имеется очередь на обслуживание (М=1), то обращаемся к подпрограмме выбора заявки на обслуживание из очереди WIB (см. работу блоков 10, 11, 12 на рис. 1.2).
В соответствии с заданной дисциплиной выбора на обслуживание осуществляется выбор заявки из очереди при условии, что прибор в такте Т свободен от обслуживания. Для заявки, выбранной на обслуживание, определяется время пребывания в очереди W и в подпрограмме набора статистических данных времени задержки в очереди STATO величина W фиксируется для набора статистических данных для дальнейшего построения кумулятивной эмпирической функции распределения времени ожидания W*(t).
Затем в алгоритме следует переход к подпрограмме определения времени обслуживания OBS (см. блок 14 на рис. 1.2). При имитации процессов (см. работу блоков 10, 11 на рис. 1.2), обслуживания прибором анализируются следующие события:
б1) обслуживание предыдущей заявки окончено, очереди нет и заявка не поступила;
б2) обслуживание окончено, заявка поступила, очередь из одной поступившей заявки;
б3) обслуживание окончено, очередь есть, заявка не поступила;
б4) обслуживание окончено, очередь есть, заявка поступила;
б5) обслуживание не окончено, очереди нет, заявка не поступила;
б6) обслуживание не окончено, очереди нет, заявка поступила;
б7) обслуживание не окончено, очередь есть, заявка не поступила;
б8) обслуживание не окончено, очередь есть, заявка поступила.
При выполнении событий б2, б3, б4 определяется время обслуживания В заявки, которая принята на обслуживание в соответствии с результатом работы подпрограммы WIB. При событиях б5 – б8 текущая величина времени обслуживания ВТ уменьшается на единицу. Текущая величина времени обслуживания ВТ введена в соответствии с динамикой изменения времени обслуживания, показанной на рис.1.1.
Затем в подпрограмме набора статистических данных времени обслуживания STATB фиксируется величина В для последующего построения кумулятивной эмпирической функции распределения времени обслуживания В*(t). К подпрограмме STATB обращение происходит только в том такте Т, в котором определено значение времени обслуживание В при занятости прибора обслуживанием (см. блоки 15, 16, 17 на рис. 1.2).
В подпрограмме STATPZ (см. блок 20 на рис. 1.2) фиксируется случайная величина PZ – длительность периода занятости для набора статистических данных кумулятивной эмпирической функции распределения периода занятости Z*(t). Обращение в подпрограмме STATPZ происходит в том случае, если заявок в очереди нет (см. блок 19 на рис. 1.2), прибор свободен от обслуживания (см. блок 15 на рис. 1.2) и подсчитанная величина PZ больше нуля.
В подпрограмме STATW фиксируется случайная величина IN – интервал времени между двумя соседними обслуженными заявками, что позволяет набирать статистические данные для дальнейшего построения кумулятивной эмпирической функции распределения длин интервалов между обслуженными требованиями D*(t).
Алгоритмы подпрограмм
Рассмотрим особенности реализации алгоритмов подпрограмм алгоритма имитационной модели одноканальной СМО.
На рис.1.3 приведена структурная схема алгоритма подпрограммы GEN.
В программе GEN событие появления заявки I=1 (см. блок 3 на рис.1.3) либо событие непоявления заявки I=0 (см. блок 4 на рис.1.3) выбираются по известной схеме моделирования случайных событий. Генерируется подпрограммой RAN случайное число x, равномерно распределенное в интервале (0,1), и сравнивается с величиной РР (см. блок 2 на рис.1.3). Если x£PP, то считается, что за такт Т поступила заявка (I=1), в противном случае принимается решение о непоступлении заявки (I=0). Величина PP из условия пуассновского распределения входного потока заявок определится PP=aΔt.

Рис.1.3
На рис.1.4 приведена структурная схема алгоритма подпрограммы STATP, который работает следующим образом.

Рис.1.4
Если в такте Т появилась на входе СМО заявка (I=1), то идентификатору ТK1 присваивается значение Т. Идентификатор TK1 принимает значение конца интервала между любыми двумя соседними заявками. Идентификатор TH1 принимает значение начала интервала. Длина интервала определится D1=TK1–TH1. Очевидно, что для определения интервала до следующей заявки, конец данного интервала станет началом следующего (см. блок 3 на рис.1.4). Затем значение D1 сравнивается с заданными границами оценок D1[J]. При выполнении условия D1£D1[J] (см. блок 6 на рис.1.4) в соответствующий счетчик K1[J] прибавляется единица. Таким образом, в счетчиках K1[J] к окончанию процесса моделирования (см.блок.23 на рис.1.2) накапливаются частоты Nj событий, состоящих в том, что длины интервалов меньше соответствующих величин D1j. Эмпирические оценки вероятностей (частости) этих событий определятся по формулам
 .
.
где N – число заявок, поступивших в СМО за время моделирования, зафиксированное в счетчике К1[JM1]; JM1 – число счетчиков К1. Заметим, что в счетчик К1[1] заносится величина D11, в счетчик К1[2] заносится величина D12, …, в счетчик К1[JM1] заносится величина D1JM1, D11<D11<…<D1JM1.
Структурная схема алгоритма подпрограммы набора статистики о потерянных заявках STATT (см. рис.1.5) аналогична схеме алгоритма подпрограммы STATP.

Рис.1.5
Информация о частотах длин интервалов между потерянными заявками накапливается в счетчиках K2[J], а в счетчиках K2[JM2] будет к последнему такту моделирования TZ получено количество потерянных заявок. Частости событий, состоящих в том, что длины интервалов D2 меньше границ оценок D2[J], определятся по формуле
 ,
,
а оценка вероятности (частость) потери заявок из-за занятости прибора и буфера очереди определится формулой
 .
.
На рис. 1.6 приведена структурная схема алгоритма подпрограммы OSTH.

Рис.1.6
Определяется номер в очереди J для поступившей заявки. Он будет на единицу больше номера JP последней заявки в очереди на обслуживание (см. блок 1 на рис.1.6). Для поступившей заявки определяется идентификатор N[J]=T (блок 2 на рис.1.6), который имеет значение, равное времени поступления этой заявки в СМО. Число заявок в очереди стало на одну больше, то есть JP=J (блок 3 на рис.1.6). Так как в очереди появилась заявка на обслуживание, то ключ М=1, а значение I=0, так как поступившая заявка «обработана» при постановке на очередь (блок 4 и блок 5 на рис.1.6).
В имитационной модели предусмотрено применение трех дисциплин выбора заявок из очереди:
- первый пришел – первый обслужен (FIFO);
- последний пришел – первый обслужен (LIFO);
- случайный выбор заявки из очереди на обслуживание (SIRO).
На рис. 1.7 приведена структурная схема алгоритма подпрограммы WIBP – выбор заявки из очереди при прямом порядке обслуживания FIFO. Работает алгоритм следующим образом.
Вызывается первый элемент массива N[1] (см. блок 1 на рис.1.7), имеющий значение времени поступления в систему заявки, первой стоящей в очереди. В предшествующем такте Т-1 прибор освободился от обслуживания (L=0) и первая из очереди заявка в такте Т принимается к обслуживанию. Следовательно, время задержки этой заявки в очереди определится W=T–N (см. блок 2 на рис.1.7).

Рис.1.7
Затем, если очередь существует (см. блок 3 на рис.1.7), необходимо «сдвинуть» массив очереди на один элемент вперед, то есть второй элемент массива становится первым, третий – вторым и т.д. (см. блоки 6, 7, 8 на рис.1.7). Затем номер последней заявки в очереди уменьшается на единицу (см. блок 9 на рис.1.7).
Очередь существует, если после выбора заявки на обслуживание номер последней заявки в очереди будет больше или равен двум (см. блок 3 на рис.1.7). Если же в очереди была одна заявки (JP=1), то ключ М=0 и число заявок в очереди JP=0.
На рис. 1.8 приведена структурная схема алгоритма подпрограммы WIBI – выбор заявки из очереди при инверсном порядке обслуживания LIFO.
При данном порядке обслуживания выбирается последняя из очереди заявка (ее номер JP) и время ее задержки в системе определится W=T–N[JP]. Число заявок в очереди после выбора уменьшается на единицу (см. блоки 1,2,3 на рис.1.8).

Рис.1.8
Затем проверяется условие наличия заявок в очереди (см. блок 4 на рис.1.8). Если заявок в очереди нет, то ключ М=0.
На рис.1.9 приведена структурная схема алгоритма подпрограммы WIBS – случайного (равновероятного) выбора заявки из очереди на обслуживание. Работает алгоритм следующим образом.
Подпрограммой RAN (см. блок 1 на рис.1.9) генерируется случайное число X, равновероятно распределенное в интервале (0,1). Затем величина этого числа приводится к длине очереди или величине интервала (0,JP). Для этого число X умножается на величину JP (см. блок 2 на рис.1.9). Полученное число X*=X´JP равновероятно распределено в интервале (0,JP).
Затем происходит поиск в схеме случайных событий. Число X* поочередно сравнивается с числом J по правилу X* £ J, где J=1,2,…,JP (см. блоки 3, 4, 5 на рис.1.9).
При первом же выполнении условия считается, что на обслуживание случайно выбрана J -я заявка. Определяется ее время задержки W=T–N[J] (см. блоки 6, 7 на рис.1.9), а затем все заявки, стоящие в очереди после J -ой, сдвигаются на один номер вперед (см. работу блоков 8, 9, 10 на рис.1.9). Затем уменьшается на одну число заявок в очереди (см. блок 11 на рис.1.9), и если число заявок в очереди равно нулю, то ключ М=0 (см. блоки 12, 13 на рис.1.9).
На рис. 1.10 приведена структурная схема алгоритма подпрограммы STATO – набора статистических данных о времени задержки заявок.
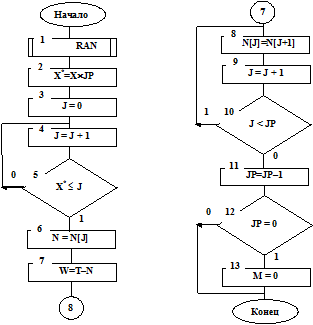
Рис.1.9

Рис.1.10
Полученная в подпрограмме WIB случайная величина W сравнивается с границами W[J] по правилу  (см. блок 2 на рис.1.10). В счетчиках K3[J] накапливается величина частоты события (см. блок 3 на рис.1.10), состоящего в том, что случайная величина W≤W[J]. Оценки вероятностей (частости) этих событий определятся по формуле
(см. блок 2 на рис.1.10). В счетчиках K3[J] накапливается величина частоты события (см. блок 3 на рис.1.10), состоящего в том, что случайная величина W≤W[J]. Оценки вероятностей (частости) этих событий определятся по формуле
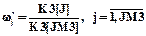 .
.
На рис. 1.11 приведена структурная схема алгоритма подпрограммы OBS - имитации обслуживания заявок прибором.

Рис. 1.11
Работает алгоритм следующим образом. Имитация длительности обслуживания должна осуществиться либо при поступлении заявки в СМО, свободную от обслуживания, либо после окончания обслуживания очередной заявки и при наличии заявок в очереди. Изменение времени обслуживания в каждом такте моделирования осуществляется идентификатором ВТ.
Если в (Т-1)-й такте не окончено время обслуживания заявки, то ВТ>0 (см. блок 1 на рис.1.11). Затем проверяется условие, не будет ли окончено обслуживание в Т -м такте (см. блоки 2, 3 на рис.1.11). Если обслуживание окончено, то формируются признаки выходного потока заявок К=1 (заявка покидает СМО обслуженной) и свободного прибора (L=0).
Если в предшествующий такт обслуживание было окончено (ВТ=0), то имитируется время обслуживания В в подпрограмме OPRB (см. блок 6 на рис.1.11) для принятой на обслуживание заявки. Время обслуживания В определяется исходя из задаваемого вида функции распределения вероятностей B(t). При имитации могут быть применены известные методы: метод обратных функций, метод ступенчатой аппроксимации и другие.
Наращивается значение идентификатора PZ – периода занятости (см. блок 7 на рис.1.11). Определяется идентификатор текущего времени ВТ=В и устанавливается признак занятости прибора L=1.
На рис. 1.12 приведена структурная схема алгоритма подпрограммы STATB – набора статистических данных о времени обслуживания заявок.
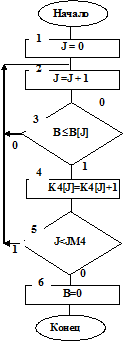
Рис.1.12
Статистические данные накапливаются в такты, при которых прибор занят и начато обслуживание очередной заявки (см. блоки 15, 16 на рис.1.2) L=1 и B>0, то есть в такты принятия заявок на обслуживание. В алгоритме подпрограммы STATB организован цикл по переменной J (см. блоки 1, 2, 5 на рис.1.12). Случайная величина В сравнивается с границами В[J], заданными с экрана дисплея (см. блок 3 на рис.1.12). В счетчиках K4[J] накапливаются величины, определяющие частоты, состоящие в том, что время обслуживания В меньше границы его оценки B[J],  .
.
Частости этих событий определяются формулой
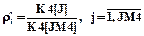 .
.
На рис. 1.13 приведена структурная схема алгоритма подпрограммы STATW – набора статистических данных выходного потока обслуженных заявок.

Рис.1.13
Набор статистических данных для исследования интервалов времени между обслуженными заявками осуществляется в такты, в которых истекает время обслуживания (L=0), обслуженная заявка покидает СМО, то есть признак наличия заявки выходного потока К=1 (см. блоки 15, 21 на рис. 1.2).
В блоках 1, 2 (см. рис.1.13) определяется интервал времени D3 между соседними обслуженными заявками. В блоке 3 начало нового интервала ТН3 между обслуженными заявками определяется как значение конца предшествующего интервала ТК3.
Логика работы алгоритма подпрограммы STATW подобного изменения значений идентификаторов ТН3, ТК3 и определения значений идентификатора D3 показана на рис.1
|
|
|


