 |
Модели СМО с очередью к каждому прибору
|
|
|
|
Рассмотрим задачу построения имитационной модели трехканальной СМО, в которой заявки, поступающие в систему, ставятся в очередь только к одному прибору и потом поступают на обслуживание к этому прибору.
Структурная схема такой СМО представлена на рис. 4.8.

Рис. 4.8
Особенностью данной СМО является распределение заявок входного потока с функцией распределения A(t) в очереди к приборам обслуживания. Непосредственно выбор заявок из очереди и обслуживание в каждом приборе моделируются так же, как и в имитационной модели одноканальной СМО.
На рис. 4.9 приведена структурная схема алгоритма имитационной модели рассматриваемой СМО. Работает алгоритм следующим образом.
Реализация алгоритма и работа подпрограммы GEN генерации заявок не отличается от реализации подпрограммы GEN для одноканальной СМО (см. рис.1.3).
Отличие состоит в том, что, если в такте Т поступила заявка в рассматриваемую систему из трех приборов обслуживания (I=1 в блоке 4 на рис. 4.9), то анализируется условие JP<JPM (см. блоки 4, 5 на рис. 4.9). Под JP понимается сумма заявок, находящихся во всех трех очередях, то есть JP=JP1+JP2+JP3.
Если это условие выполняется, то управление передается подпрограмме набора статистических данных входного протока STATP и затем подпрограмме распределения заявок по очередям к приборам ROSTH (см. блоки 3, 4, 5,10, 11 на рис. 4.9). Если условие не выполняется, но есть хотя бы один из приборов, свободный от обслуживания, то заявка также не теряется (см. работу алгоритма по блокам 3, 4, 5, 6, 7, 8, 10, 11 на рис. 4.9).
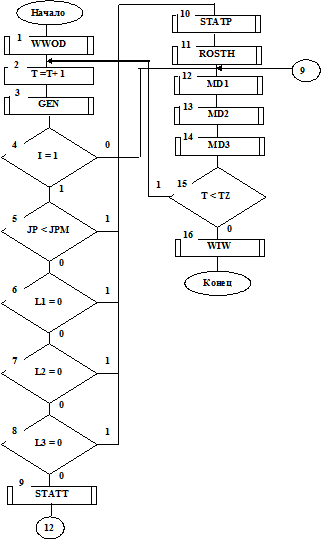
Рис.4.9
В противном случае, после работы алгоритма по блокам 3, 4, 5, 6, 7, 8, управление передается подпрограмме набор статистических данных потока потерянных заявок STATT.
|
|
|
Особенности алгоритма модели данной СМО состоят в реализации вариантов алгоритмов подпрограммы ROSTH. В СМО могут быть следующие правила распределения заявок по приборам обслуживания:
а) к прибору с меньшей очередью;
б) случайным образом;
в) по порядку следования номеров приборов;
г) преимущественно к прибору с меньшим средним временем обслуживания.
Очевидно, что могут существовать другие правила распределения заявок к приборам.
На рис. 4.10 приведена структурная схема алгоритма подпрограммы ROSTHM распределения заявок к приборам с меньшей очереди.

Рис.4.10
Как видно из схемы алгоритма, в нем существуют логические переходы, определенные состояниями очередей к приборам. В табл. 4.2 приведены комбинации возможных состояний очередей к приборам и действие алгоритма подпрограммы ROSTHM по выбору приборов при постановке поступившей заявки в очередь.
Таблица 4.2
| JP1= JPМ1 | JP2= JPM2 | JP3= JPM3 | JP1<JP2<JP3 JP1<JP3<JP2 | JP2<JP1<JP3 JP2<JP3<JP1 | JP3<JP1<JP2 JP3<JP2<JP1 | Действие |
| Заявка к 3-му прибору | ||||||
| Заявка ко 2-му прибору | ||||||
| Заявка к 1-му прибору | ||||||
| Заявка ко 2-му прибору | ||||||
| Заявка к 1-му прибору | ||||||
| Заявка к 3-му прибору | ||||||
| Заявка к 1-му прибору | ||||||
| Заявка к 3-му прибору | ||||||
| Заявка ко 2-му прибору | ||||||
| Заявка к 1-му прибору | ||||||
| Заявка ко 2-му прибору | ||||||
| Заявка к 3-му прибору | ||||||
| Заявка к прибору, идентификатор занятости L которого равен нулю. |
В случае если максимально допустимые емкости очередей к каждому прибору одинаковые JPM1=JPM2=JPM3, то необходимость в блоках 16, 17, 18 (см. рис. 4.10) отпадает и выходы блоков 10, 11, 12 подаются на вход блока 13.
|
|
|
Рассмотрим на некоторых примерах, как реализованы логические переходы в алгоритме подпрограммы ROSTHM при анализе состояний приборов и очередей заявок к приборам обслуживания.
Пусть, например, поступила заявка и очереди ко всем приборам заполнены полностью, заняты обслуживанием первый и второй приборы, но в текущем такте Т освобождается от обслуживания третий прибор (последняя сторока в табл.4.2).
В этом случае работа алгоритма происходит последовательно по блокам 1, 2, 3, 4, 6, 8, 9 (см. рис.4.10). В результате заявка будет поставлена в очередь к третьему прибору обслуживания (см. блоки 8, 9 на рис. 4.10).
Пусть сложилась такая ситуация, что очереди в первом и втором приборе одинаковы, меньше их наибольшего значения и меньше очереди к третьему прибору обслуживания. В этом случае работа алгоритма происходит последовательно по блокам 1, 9, 10, 13, 15, 5, 19 (см. рис.4.10). В результате поступившая в систему заявка будет поставлена в очередь к первому прибору обслуживания (см. блоки 5, 19 на рис. 4.10).
Если же очередь к первому прибору меньше наибольшего значения JPM1, больше очереди ко второму прибору, а очереди к первому и второму приборам меньше очереди к третьему прибору обслуживания, то работа алгоритма происходит последовательно по блокам 1, 9, 10, 16, 7, 20 (см. рис.4.10). В результате поступившая в систему заявка будет поставлена в очередь ко второму прибору обслуживания (см. блоки 7, 20 на рис. 4.10).
На рис. 4.11 приведена структурная схема алгоритма подпрограммы ROSTHS распределения заявок к прибором случайным образом. Работает алгоритм следующим образом.
Вначале проверяются условия, при которых в очередях к приборам обслуживания имеются свободные места JP1<JPM1, JP2<JPM2, JP3<JPM3 (см. блоки 1 – 3 на рис. 4.11). Если все эти условия выполняются, то равновероятно выбирается одна из очередей (см. работу блоков 4, 5, 6, 7 на рис. 4.11). То есть генерируется число Х, равномерно распределенное в интервале (0,1), которое затем приводится к отрезку (0,3). Если Х меньше либо равно единице, то заявка ставится в очередь к первому прибору (см. блоки 8, 20 на рис.4.11). Если Х меньше либо равно двум, то заявка ставится в очередь ко второму прибору (см. блоки 9, 21 на рис.4.11). Если Х меньше либо равно трем, то заявка ставится в очередь к третьему прибору (см. блоки 10, 22 на рис.4.11).
|
|
|
Если JP1=JPM1, JP2<JPM2, JP3<JPM3, то равновероятно выбираются второй и третий приборы обслуживания (см. работу алгоритма по блокам 1, 11, 12, 13, 14 на рис. 4.11). Если JP1<JPM1, JP2=JPM2, JP3<JPM3, то равновероятно выбирается первый и третий приборы (см. работу блоков 1, 2, 17, 18, 19 на рис. 4.11).
Если из трех неравенств выполняется только одно, то заявка направляется к соответствующему прибору обслуживания. Например, при JP1<JPM1, JP2=JPM2, JP3=JPM3 заявка будет поставлена в очередь к первому прибору обслуживания (см. работу алгоритма по блокам 1, 2, 17, 8, 20 на рис. 4.11).

Рис.4.11
На рис. 4.12 приведена структурная схема алгоритма подпрограммы ROSTHN распределения заявок в соответствии со следованием порядков номеров приборов обслуживания при неограниченных длинах очередей.
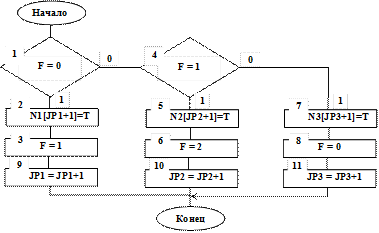
Рис. 4.12
Принцип реализации алгоритма распределения заявок к приборам в соответствии с их порядковыми номерами основан на запоминании номеров прибора, в которых была направлена заявка. Следующая заявка будет направлена в прибор, номер которого на единицу больше. Для этого вводится ключ F.
Если значение ключа F=0, то заявка направлена в очередь к первому прибору (см. работу блоков 1, 2 на рис. 4.12). После чего значение F=1 и число заявок в очереди к первому прибору увеличивается на единицу (см. работу блоков 3, 9на рис. 4.12).
Если значение ключа F=1, то заявка направлена в очередь ко второму прибору (см. работу блоков 1, 4, 5 на рис. 4.12). После чего значение F=2 и число заявок в очереди ко второму прибору увеличивается на единицу (см. работу блоков 6, 10 на рис. 4.12).
Если значение ключа F не равно ни нулю, ни единице, то заявка направлена в очередь к третьему прибору (см. работу блоков 1, 4, 7). После чего значение F=0 и число заявок в очереди к третьему прибору увеличивается на единицу (см. работу блоков 8, 11на рис. 4.12).
После работы подпрограммы ROSTH управление (см. рис. 4.9) передаётся подпрограммам MD1, MD2, MD3, в которых моделируются процессы обслуживания в каждом из каналов. Реализация каждой из подпрограмм одинакова и представляет собой последовательность блоков 9 – 22 имитационной модели одноканальной СМО (см. рис.1.2).
|
|
|
|
|
|


