 |
Как осуществляется классификация СМО?
|
|
|
|
СМО классифицируют следующим образом.
По потокам заявок СМО делятся на СМО с однородным потоком и приоритетные СМО.
По дисциплинам обслуживания СМО делятся на СМО с дисциплиной FIFO (первый пришел - первый обслуживается), СМО с дисциплиной LIFO (последний пришел - первый обслуживается), СМО со случайным выбором на обслуживание.
Исходя из того, каким временем на ожидание располагает заявка, СМО делятся на СМО с отказами, если эта величина времени ожидания равна нулю; смешанные СМО, если время ожидания является конечной величиной (СМО с ограниченной очередью); СМО с ожиданием, если время ожидания является бесконечной величиной (с бесконечной очередью).
По количеству и структурному расположению приборов обслуживания СМО делятся на одноканальные, если имеется один прибор обслуживания; n -канальные, если имеются n параллельно расположенных приборов; m -фазные СМО, если имеются последовательно расположенные m приборов; СМО смешанной структуры. Классификация может быть осуществлена, исходя из математических законов, описывающих математические модели потока входных заявок и времени обслуживания.
Дайте определение простому потоку заявок.
Простейший поток (поток Пуассона) удовлетворяет условиям:
- ординарный поток, если за сколь угодно малый отрезок времени вероятность появления двух и более заявок равна нулю;
- стационарный поток, если вероятность поступления k -заявок за интервал времени (t0,t) не зависит от выбора момента t0;
- поток без последействия, если вероятность появления k -заявок внутри некоторого интервала не зависит от появления заявок до момента начала этого интервала.
Для простого потока вероятность поступления k -событий за время t определится
|
|
|

Функция распределения времени поступления между двумя заявками определяется экспоненциальным распределением - A(t)=1-e-lt.
Какие теоретические распределения наиболее часто применяются для аппроксимации эмпирических распределений входных потоков заявок, времени обслуживания?
Распределение Пуассона

Экспоненциальное распределение времени поступления между двумя заявками
A(t)=1-e-lt.
Функция распределения плотности вероятности интервалов между заявками для эрланговского потока r-го порядка
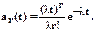
Гауссово распределение, описывающее нормальный эргодический поток с нулевым математическим ожиданием. Одномерная плотность вероятности этого процесса имеет вид
 .
.
От нормального распределения можно перейти к распределению с не нулевым математическим ожиданием.
Релеевское распределение потока заявок с плотностью вероятности заявок

Поток заявок может быть регулярным, с постоянным временным интервалом между поступающими заявками.
Что такое период занятости СМО?
Отрезки времени, в течение которых прибор обслуживания непрерывно занят обслуживанием поступающих заявок.
Приведите пример временных диаграмм, иллюстрирующих процесс функционирования СМО.
Выведите модель одноканальной СМО с пуассоновским потоком заявок и экспоненциальным распределением времени обслуживания в виде уравнений Эрланга.
См. [7. С. 58 - 60]
Дайте определение коэффициента использования СМО.
Коэффициент использования r СМО определяется как отношение интенсивности входного потока заявок l (число заявок поступающих в СМО в единицу времени) к интенсивности обслуживания заявок m (число заявок обслуживаемых в СМО в единицу времени). При r³1 очередь в СМО неограниченно возрастает.
|
|
|


