Главная | Обратная связь | Поможем написать вашу работу!

Статистические методы изучения уровней динамики

Основная цель статистического изучения динамики коммерческой деятельности состоит в выявлении и измерении закономерностей их развития во времени. Это достигается посредством построения и анализа статистических рядов динамики.

Рядами динамики называются статистические данные, отображающие развитие изучаемого явления во времени. В каждом ряду динамики имеются два основных элемента: показатель времени t; соответствующие им уровни развития изучаемого явления у. В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты) времени, либо отдельные периоды (годы, кварталы, месяцы, сутки).

Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами.

В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим, ряды динамики подразделяются на моментные и интервальные.

Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени.

Примером моментного ряда динамики является следующая информация о списочной численности работников фирмы N в 1994 г.:

Дата	1.01	1.04	1.07	1.10	1.01
Год	1994 г.	1994 г.	1994 г.	1994 г.	1995 г.
Число работников, чел.	192	190	195	198	200

Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности. Так, основная часть персонала фирмы N, составляющая списочную численность на 1.01.1994г., продолжающая работать в течение данного года, отображена в уровнях последующих периодов. Поэтому при суммировании уровней моментного ряда динамики может возникнуть повторный счет.

Интервальные ряды динамики отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени.

Примером интервального ряда динамики могут служить данные о розничном товарообороте магазина в 1990-1994 гг.:

Год	1990	1991	1992	1993	1994
Объем розничного товарооборота, тыс. руб.	885,7	932,6	980,1	1028,7	1088,4

Особенностью интервального ряда динамики является то, что каждый его уровень складывается из данных за более короткие интервалы времени. Например, суммируя товарооборот за первые три месяца года, получают его объем за I квартал, а сумма товарооборота четырех кварталов дает объем товарооборота за год и т.д.

Ряды динамики могут быть полными и неполными.

Полный ряд - ряд динамики, в котором одноименные моменты времени или периоды времени строго следуют один за другим в календарном порядке или равноотстоят друг от друга.

Неполный ряд динамики - ряд, в котором уровни зафиксированы в неравноотстоящие моменты или периоды времени.

Пример.

Численность населения СССР характеризуется данными переписей, млн. чел.:

1939 1959 1970 1979 неполный моментный ряд

170,6 208,8 241,7 262, 4 абсолютных величин

Приведение рядов динамики в сопоставимый вид.

Ряды динамики, изучающие изменение статистического показателя, могут охватывать значительный период времени, на протяжении которого могут происходить события, нарушающие сопоставимость отдельных уровней ряда динамики (изменение методологии учета, изменение цен и т.д.).

Для того, чтобы анализ ряда был объективен, необходимо учитывать события, приводящие к несопоставимости уровней ряда и использовать приемы обработки рядов для приведения их в сопоставимый вид.

Наиболее характерные случаи несопоставимости уровней ряда динамики:

Территориальные изменения объекта исследования, к которому относится изучаемый показатель (изменение границ городского района, пересмотр административного деления области и т.д.).

Разновеликие интервалы времени, к которым относится показатель. Так, например, в феврале - 28 дней, в марте - 31 день, анализируя изменения показателя по месяцам, необходимо учитывать разницу в количестве дней.

Изменение даты учета. Например, численность поголовья скота в разные годы могла определяться по состоянию на 1 января или на 1 октября, что в данном случае приводит к несопоставимости.

Определение среднего уровня ряда динамики.

В качестве обобщенной характеристики уровней ряда динамики служит средний уровень ряда динамики 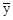. В зависимости от типа ряда динамики используются различные расчетные формулы.

Интервальный ряд абсолютных величин с равными периодами (интервалами времени):

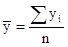
Моментный ряд с равными интервалами между датами:

Моментный ряд с неравными интервалами между датами:

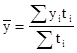
где - уровни ряда, сохраняющиеся без изменения на протяжении интервала времени .

Показатели изменения уровней ряда динамики.

Одним из важнейших направлений анализа рядов динамики является изучение особенностей развития явления за отдельные периоды времени.

С этой целью для динамических рядов рассчитывают ряд показателей:

К - темпы роста;

- абсолютные приросты;

- темпы прироста.

Темп роста - относительный показатель, получающийся в результате деления двух уровней одного ряда друг на друга. Темпы роста могут рассчитываться как цепные, когда каждый уровень ряда сопоставляется с предшествующим ему уровнем: , либо как базисные, когда все уровни ряда сопоставляются с одним и тем же уровнем , выбранным за базу сравнения: . Темпы роста могут быть представлены в виде коэффициентов либо в виде процентов.

Абсолютный прирост - разность между двумя уровнями ряда динамики, имеет ту же размерность, что и уровни самого ряда динамики. Абсолютные приросты могут быть цепными и базисными, в зависимости от способа выбора базы для сравнения:

цепной абсолютный прирост

;

базисный абсолютный прирост

Для относительной оценки абсолютных приростов рассчитываются показатели темпов прироста.

Темп прироста - относительный показатель, показывающий на сколько процентов один уровень ряда динамики больше (или меньше) другого, принимаемого за базу для сравнения.

Базисные темпы прироста:

Цепные темпы прироста:

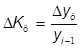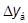и - абсолютный базисный или цепной прирост;

- уровень ряда динамики, выбранный за базу для определения базисных абсолютных приростов;

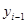- уровень ряда динамики, выбранный за базу для определения i-го цепного абсолютного прироста.

Существует связь между темпами роста и прироста:

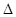К = К - 1 или 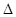К = К - 100 % (если темпы роста определены в процентах).

Если разделить абсолютный прирост (цепной) на темп прироста (цепной) за соответствующий период, получим показатель, называемый - абсолютное значение одного процента прироста:

Определение среднего абсолютного прироста,

средних темпов роста и прироста.

По показателям изменения уровней ряда динамики (абсолютные приросты, темпы роста и прироста), полученным в результате анализа исходного ряда, могут быть рассчитаны обобщающие показатели в виде средних величин - средний абсолютный прирост, средний темп роста, средний темп прироста.

Средний абсолютный прирост может быть получен по одной из формул:

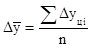или ,

где n - число уровней ряда динамики;

- первый уровень ряда динамики;

- последний уровень ряда динамики;

- цепные абсолютные приросты.

Средний темп роста можно определить, пользуясь формулами:

где n - число рассчитанных цепных или базисных темпов роста;

- уровень ряда, принятый за базу для сравнения;

- последний уровень ряда;

- цепные темпы роста (в коэффициентах);

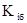- первый базисный темп роста;

- последний базисный темп роста.

Между темпами прироста и темпами роста К существует соотношение = К - 1, аналогичное соотношение верно и для средних величин.

Определение общей тенденции развития.

Определение уровней ряда динамики на протяжении длительного периода времени обусловлено действием ряда факторов, которые неоднородны по силе и направлению воздействия, оказываемого на изучаемое явление.

Рассматривая динамические ряды, пытаются разделить эти факторы на постоянно действующие и оказывающие определяющее воздействие на уровни ряда, формирующие основную тенденцию развития, и случайные факторы, приводящие к кратковременным изменениям уровней ряда динамики. Наиболее важна при анализе ряда динамики его основная тенденция развития, но часто по одному лишь внешнему виду ряда динамики ее установить невозможно, поэтому используют специальные методы обработки, позволяющие показать основную тенденцию ряда. Методы обработки используются как простые, так и достаточно сложные. Простейший способ обработки ряда динамики, применяемый с целью установления закономерностей развития - метод укрупнения интервалов.

Суть метода в том, чтобы от интервалов, или периодов времени, для которых определены исходные уровни ряда динамики, перейти к более продолжительным периодам времени и посмотреть, как уровни ряда изменяются в этом случае.

Другой способ определения тенденции в ряду динамики — метод скользящих средних. Суть метода заключается в том, что фактические уровни ряда заменяются средними уровнями, вычисленными по определённому правилу, например:

— исходные или фактические уровни ряда динамики заменяются средними уровнями:

...

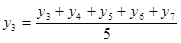
В результате получается сглаженный ряд, состоящий из скользящих пятизвенных средних уровней . Между расположением уровней и устанавливается соответствие:

— — — —,

сглаженный ряд короче исходного на число уровней 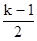, где k - число уровней, выбранных для определения средних уровней ряда.

Сглаживание методом скользящих средних можно производить по четырём, пяти или другому числу уровней ряда, используя соответствующие формулы для усреднения исходных уровней.

Полученные при этом средние уровни называются четырёхзвенными скользящими средними, пятизвенными скользящими средними и т.д.

При сглаживании ряда динамики по чётному числу уровней выполняется дополнительная операция, называемая центрированием, поскольку, при вычислении скользящего среднего, например по четырём уровням, относится к временной точке между моментами времени, когда были зафиксированы фактические уровни и . Схема вычислений и расположений уровней сглаженного ряда становится сложнее:

... — исходные уровни;

— — ... — сглаженные уровни;

— — ... — центрированные сглаженные уровни;

Метод скользящих средних не позволяет получить численные оценки для выражения основной тенденции в ряду динамики, давая лишь наглядное графическое представление (пример 1).

Наиболее совершенным способом определения тенденции развития в ряду динамики является метод аналитического выравнивания. При этом методе исходные уровни ряда динамики заменяются теоретическими или расчетными , которые представляют из себя некоторую достаточно простую математическую функцию времени, выражающую общую тенденцию развития ряда динамики. Чаще всего в качестве такой функции выбирают прямую, параболу, экспоненту и др.

Например, ,

где - коэффициенты, определяемые в методе аналитического выравнивания;

- моменты времени, для которых были получены исходные и соответствующие теоретические уровни ряда динамики, образующие прямую, определяемую коэффициентами .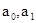

Расчет коэффициентов ведется на основе метода наименьших квадратов:

Если вместо 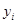подставить (или соответствующее выражение для других математических функций), получим:

Это функция двух переменных (все и известны), которая при определенных достигает минимума. Из этого выражения на основе знаний, полученных в курсе высшей математики об экстремуме функций n переменных, получают значения коэффициентов .

Для прямой:

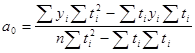
где n — число моментов времени, для которых были получены исходные уровни ряда .

Если вместо абсолютного времени выбрать условное время таким образом, чтобы , то записанные выражения для определения упрощаются:

РАЗДЕЛ 2

Практическая часть

Имеются следующие выборочные данные по предприятиям из отраслей промышленности в отчетном году (выборка 20-% механическая)

№ предприятия по п/п	выпуск продукции, тыс.ед.	затраты на производство продукции, млн.руб	№ предприятия по п/п	выпуск продукции, тыс.ед.	затраты на производство продукции, млн.руб
1	160	18,240	16	148	17,612
2	140	17,080	17	110	13,970
3	105	13,440	18	146	17,666
4	150	17,850	19	155	17,980
5	158	18,170	20	169	19,260
6	170	19,210	21	156	17,940
7	152	17,936	22	135	16,335
8	178	19,580	23	122	15,250
9	180	19,440	24	130	15,860
10	164	18,860	25	200	21,000
11	151	17,818	26	125	15,250
12	142	17,040	27	152	17,784
13	120	15,000	28	173	19,030
14	100	13,000	29	115	14,490
15	176	19,360	30	190	19,950

Задание 1

Признак- себестоимость единицы продукции. Число групп –пять.

1. постройте статистический ряд распределения организации по признаку, образовав заданное число групп с равными интервалами.

2. постройте графики распределения полученных рядов. Графически определить значений моды и медианы.

3. рассчитайте характеристики интервального ряда распределения- среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации.

4. вычислить среднюю арифметическую по исходным данным, сравните ее с аналогичным показателем, рассчитываемым в пункте три для интервального ряда распределения. Объяснить причину расхождения.

5. Сделать вывод.

Задание 2

1.связь между признаками - выпуск продукции и себестоимость единицы продукции. Установить наличие и характер связи между признаками, образовав заданное число групп с равными интервалами по обеим признакам, методами:

1.) Аналитической группировки

2.) корреляционной таблицы.

Задание 3

По результатам выполнения задания 1 с вероятностью 0,954 определите:

1.ошибку выборки среднего уровня себестоимости единицы продукции и границы, в которых будет располагаться средний уровень генеральной совокупности.

2. ошибку выборки доли предприятий с уровнем себестоимости единицы продукции 125 тыс.руб. и более, и границы, в которых будет находиться генеральная доля.

Задание 4

Имеются данные о выпуске однородной продукции и ее себестоимости по двум филиалам фирмы:

филиал	базисный период		отчетный период
филиал	выпуск продукции тыс.руб.	себестоимость продукции тыс. руб.	выпуск продукции тыс.руб.	себестоимость продукции тыс.руб.
1	20	2	31,5	2,5
2	20	2,1	10,5	2,7

Итого