Тензор конечных деформаций

Рассмотрим произвольно ориентированный бесконечно ма­лый отре­зок внутри деформируемого тела, ограниченный точ­ками 1{ x, y, z } и 2{ x + dx, y + dy, z + dz } (рис. 8). Под действием внеш­них сил концы отрез­ка получают некоторые переме­ще­ния, которые предполагаются непре­рывными функциями коор­ди­нат. Обозначим проекции вектора перемеще­ния точки 1 по осям координат x, y, z соответственно u (x, y, z), v (x, y, z), w (x, y, z). Тогда компоненты перемещения второго конца отрезка соста­вят u + du, v + dv, w + dw, а координаты точек 1 и 2 после де­фор­мации будут 1’{ x + u, y + v, z + w }; 2’{ x + dx + u + du, y + dy + v + d v, z + dz + w + dw }.

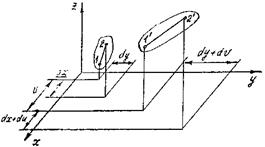
Рис. 8 Конечная деформация бесконечно малого отрезка внутри деформируемого тела

Для определения приращений du, dv, dw воспользуемся по­ня­тием дифференциала функции трех независимых перемен­ных (1.48)

;

; (1.52)

Различные меры деформации основаны на сравнении тех или иных геометрических характеристик в исходном и ко­неч­ном состояниях. С этой целью можно сравнивать длины, пло­ща­ди или объемы. Тензор конечных деформаций основан на сравнении квадратов длины. В ис­ходном состоянии

. (1.53)

Квадрат длины рассматриваемого отрезка после деформа­ции соста­вит

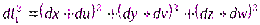
или с учетом приращений (1.52)

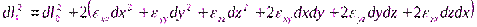(1.54)

где

;

;

; (1.55)

;

;

.

По предложению Грина [6], за меру деформации можно принять отношение

. (1.56)

Переходя от проекций длины отрезка в исходном состоянии dx, dy, dz к его направляющим косинусам

,

уравнение (1.54) можно представить в виде

. (1.57)

Сравнение уравнений (1.57) и (1.14) позволяет утверждать, что компоненты , характеризующие деформацию сплошной сре­ды в ок­рестности рассматриваемой точки, образуют сим­мет­рич­ный тензор второго ранга

, (1.58)

который называют тензором конечной деформации Грина.

Если воспользоваться индексными обозначениями для ком­по­нент вектора перемещения

, (1.59)

тогда тензор (1.58) с компонентами (1.55) можно записать в крат­ком виде

, (1.60)

суммирование в правой части проводится только по индексу k, так как другие индексы в одночленах не повторяются.

Тензор малых деформаций

В области упругих и упругопластических деформаций для боль­шин­ства металлов компоненты малы по сравнению с еди­ницей, и в уравнениях (1.55) квадратами производных, а так­же их произведени­ями можно пренебречь. Тогда вместо (1.60) получим тензор

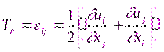, (1.61)

который называют тензором малых деформаций Коши.

В технических приложениях обычно используют обозначе­ния

; (1.62)

,

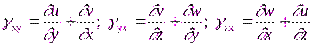при этом тензор малых деформаций принимает вид

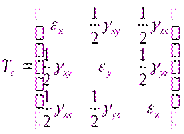. (1.63)

Компоненты (1.62) имеют простой геометрический смысл и харак­теризуют деформацию волокон, первоначально парал­лель­­ных осям ко­ординат. На рис. 9 показана проекция одной грани параллелепипеда на плоскость x - y (с длинами ребер dx и dy в исходном состоянии) до и после деформации.

Рис. 9 Линейные и угловые деформации

Из соотношения (1.58) при условии dl ₀ dl ₁ следует, что ком­­поненты тензора (1.63), расположенные на главной диа­го­на­ли, опре­деляют относительное растяжение или сжатие (при < 0) ребер параллелепипеда

. (1.64)

Действительно, считая поворот ребер незначительным, для сто­­ро­ны ab можно записать

.

Аналогичным образом, разность перемещений концов от­рез­ка ac в направлении оси y, отнесенная к его начальной длине dy, определя­ет деформацию e_y.

С другой стороны, сумма углов поворота сторон ab и ac

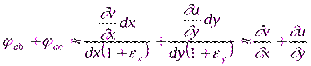
определяет деформацию сдвига или искажение первоначально пря­мого угла

.

Компоненты тензора 0,5 представляют усредненные сдви­ги граней параллелепипеда.

Так как компоненты малой деформации (1.62) образуют сим­­метрич­ный тензор второго ранга, для них справедливы все соотношения, полученные в разд. 1.1 для тензора напряжений. В частности, в окрестности любой точки деформированного тела можно выделить три главных направления, вдоль которых деформации сдвига отсутствуют, а деформации растяжения или сжатия достигают экстремальных значе­ний и называются главными деформациями , , 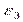. Тензор дефор­мации в глав­ных осях имеет вид

. (1.65)

Тензор деформации имеет три инварианта

, (1.66)

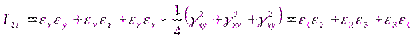, (1.67)

, (1.68)

которые не зависят от выбора осей координат и могут быть ис­поль­зованы для описания физических закономерностей про­цес­сов деформа­ции.

Линейный инвариант характеризует относительное измене­ние объе­ма бесконечно малого параллелепипеда. Если его ори­ен­тировать по главным осям и обозначить исходные размеры a ₀, b ₀, h ₀, тогда, в соответствии с определением (1.64), конечные размеры составят

a ₁= a ₀(1+ ); b₁=b₀ (1+ ); h₁=h₀ (1+ ).

Следовательно,

(1.69)

и для несжимаемой среды должно выполняться условие

= 0. (1.70)

Тензор деформации можно разложить на шаровой тензор и девиатор

= + ; . (1.71)

Диагональные компоненты шарового тензора равны средней дефор­мации

. (1.72)

и характеризуют объемное расширение среды.

Для несжимаемых материалов шаровой тензор деформации равен нулю, а девиатор совпадает с полным тензором .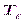

В плоскостях, которые проходят через одно из главных нап­равле­ний и делят пополам углы между другими главными нап­рав­лениями, сдвиги достигают экстремальных значений и на­зы­ваются главными деформациями сдвига

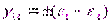; ; . (1.73)

Для тензора деформации можно построить круги Мора, оп­ре­делить параметр Лодэ-Надаи [3-6].

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: