Остаточные напряжения, их роль при ОМД, методы их устранения

37) Закон был сформулирован С.И. Губкина: в случае возможного перемещения точек деформируемого тела в различных направлениях, каждая точка деформируемого тела перемещается в направлении наименьшего сопротивления. Пользуясь законом можно определить любую форму и размеры поперечного сечения получить заготовку квадратного, прямоугольного или любого сечения в процессе пластического формообразования.

Предположим, что свободной осадке подвергается заготовка квадратного сечения (рис. 1.14, а). В плоскости поперечного сечения осаждаемых заготовки проведем биссектрисы углов, что в данном случае является одновременно диагоналями. Очевидно, что каждая частица данного участка пересечения перемещаться по перпендикуляру к стороне периметра, как указано на рис.1.14., a стрелками. Также очевидно, что поток частиц, перемещающихся в центральных частях будет больше, чем в периферийных (вблизи углов). Поэтому сечение заготовки примет такую форму, как показано на рис. 1.14, а штриховой линией. При продолжении деформации настоящее сечение превратится в круг, поскольку при данной площади сечения заготовки круг имеет наименьший периметр. Рассуждая таким же образом, нетрудно доказать, что при осадке заготовки прямоугольного сечения ее пересечение стремиться к эллипсу (рис. 1.14, б). При осадке цилиндрической заготовки ее пересечение оставаться круглым. Искажение формы поперечного сечения заготовок, деформируются, связано с наличием контактного трения. Рисунок 1.14. Сечение квадратного и прямоугольного образцов до и после осадки (штриховая линия) Закон наименьшего сопротивления справедлив только при больших значениях коэффициента трения, если же он мал, то частицы в горизонтальных поперечных сечениях перемещаться не по нормали к периметру, а по лучах, проведенных из центра симметрии сечения. Закон имеет большое значение при всех технологических процессах обработки давлением. Он позволяет рационально подбирать форму поперечного сечения заготовок для конкретных случаев пластической деформации. На основании закона наименьшего периметра возможно применение заготовок квадратного сечения при штамповке поковок осадкой, имеющие в плане круглое сечение.

38) Уравнения равновесия показывают зависимость напряжений от координат, В общем случае объемного напряженного состояния имеем три уравнения равновесия:

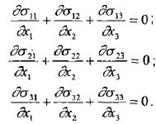
Уравнение пластичности связывает напряжения, необходимые для осуществления пластической деформации, с физическими свойствами деформируемого тела (сопротивление деформации σт).

Эти уравнения содержат 6 неизвестных (три нормальных и три касательных). Число уравнений меньше числа неизвестных. Присоединим к ним шесть уравнений связи (между напряжениями и деформациями):

(связь между модулями G' = Е'/З) и три уравнения неразрывности деформации:

B последних девяти уравнениях содержатся еще семь неизвестных: три линейные деформации, три деформации сдвига, модуль деформации второго рода G' (или модуль пластичности E').
В результате для объемного напряженного состояния имеем 13 уравнений с 13-ю неизвестными.
Решение этой системы уравнений в принципе возможно, так как число уравнений равно числу неизвестных, но практически эта задача не разрешима из-за большого числа неизвестных в частных производных.
Задача упрощается для частных случаев напряженно-деформированного состояния.
Для осесимметричного напряженного состояния имеем два уравнения равновесия, одно уравнение пластичности, четыре уравнения связи и одно уравнение неразрывности деформаций. Итого восемь уравнений с 8-ю неизвестными.

Для плоского напряженного и плоского деформированного состояний имеем два уравнения равновесия

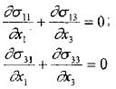
и одно уравнение пластичности: - для плоского напряженного состояния

- для плоского деформированного состояния

где σ11, σ33 - нормальные напряжения на произвольной площадке; σ13 - касательное напряжение; k - постоянная пластичности - максимальное касательное напряжение (сопротивление чистому сдвигу при пластическом деформировании). k=σт/√3.
Всего три уравнения с тремя неизвестными.
Несмотря на эти значительные упрощения задачи для осесимметричного, плоского напряженного или плоского деформированного состояния, для данных случаев также решено ограниченное число задач,
Более широкое применение получил метод совместного решения приближенных уравнений равновесия и уравнения пластичности (инженерный метод). Его широко применяют для расчета усилий и расхода энергии при ОМД.

39) Рассмотрим процесс осаживания металла между двумя плоскими бойками. Работа равна произведению силы на путь. Полная сила, производящая деформацию, определяется произведением удельного давления на площадь соприкосновения металла с бойком. Эта площадь меняется в процессе деформации, увеличиваясь от F₁ в начальный момент, до F₂ в конечный момент сжатия. Удельное давление, т.е. сжимающие усилие, отнесенное к единице площади, принимаем постоянным.

40) Реализация технологии волочения сверхпроводящей композитной заготовки требует знания температурных условий деформирования. При многократном волочении температура заготовки изменяется за счет деформационного разогрева в каждом проходе и определяется условиями охлаждения между проходами. Знание температурного режима необходимо для оценки термоупругого состояния многокомпонентной заготовки, предотвращения возможного отслоения оболочки от сердечника.

Для определения разогрева металла проволоки при деформации необходимо определить работу, затраченную на деформацию, в виде

,

где - сопротивление деформации, зависящее в общем случае от степени деформации.

Если принять, что вся работа пластической деформации переходит в тепло, то повышение температуры для единицы объема материального элемента в течение адиабатного процесса деформирования определится уравнением

,

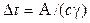где с – удельная теплоемкость протягиваемого металла; – плотность металла.