Главная | Обратная связь | Поможем написать вашу работу!

Теоретическая основа линейного программирования

Постановка задачи

Постановка практической задачи ЛП включает следующие основные этапы:

· определение показателя эффективности, переменных задачи,

· задание линейной целевой функции S(x), подлежащей минимизации или максимизации,

· задание ограничений.

Приведем сейчас общую математическую формулировку основной задачи линейного программирования.

Дана система линейных уравнений с n неизвестными:

a11 x1 + a11 x2 + …… + a11 xn = b1,

a21 x1 + a22 x2 + …… + a2n xn = b2,

am1 x1 + am2 x2 + …… + amn xn = bm,

и линейная функция

f = c1 x1 + c2 x2 +………+ cn xn (1.2)

Требуется найти такое неотрицательное решение системы

x1 ≥0, x2 ≥0, … …, xn ≥0 (1.3)

при котором функция f принимает наименьшее значение.

Уравнения (1.1) называют системой ограничений данной задачи; функцию f — целевой функцией (или линейной формой).

Методы решения задач линейного программирования

Симплекс – метод

Симплекс метод - метод линейного программирования, который реализует рациональный перебор базисных допустимых решений, в виде конечного итеративного процесса, необходимо улучшающего значение целевой функции на каждом шаге.

Применение симплекс-метода для задачи линейного программирования предполагает предварительное приведение ее формальной постановки к канонической форме с n неотрицательными переменными: (X1,..., Xn), где требуется минимизация линейной целевой функции при m линейных ограничениях типа равенств. Среди переменных задачи выбирается начальный базис из m переменных, для определенности (X1,..., Xm), которые должны иметь неотрицательные значения, когда остальные (n-m) свободные переменные равны 0. Целевая функция и ограничения равенства преобразуются к диагональной форме относительно базисных переменных, переменных, где каждая базисная переменная входит только в одно уравнение с коэффициентом 1:

X₀ + A_0,m+1*X_m+1 +... + A_0,n*X_n = A_0,0 X₁ + A_1,m+1*X_m+1 +... + A_1,n*X_n = A_1,0 .. ............... . X_i + A_i,m+1*X_m+1 +... + A_i,n*X_n = A_i,0 . . ............... . X_m + A_m,m+1*X_m+1 +... + A_m,n*X_n = A_m,0

Данная формальная модель задачи линейного программирования обычно задается в форме так называемой симплекс-таблицы, удобной для выполнения операций симплекс-метода:

Симплекс-таблица

	1	X₁	X₂	...	X_m	X_m+1	...	X_n
X₀	A_0,0	0	0	...	0	A_0,m+1	...	A_0,n
X₁	A_1,0	1	0	...	0	A_1,m+1	...	A_1,n
X₂	A_2,0	0	1	...	0	A_2,m+1	...	A_2,n
...	...	...	...	...	...	...	...	...
X_m	A_m,0	0	0	...	1	A_m,m+1	...	A_m,n

Верхняя строка симплекс-таблицы представляет целевую функцию задачи. Каждая строка симплекс-таблицы, кроме первой, соответствует определенному ограничению-равенству задачи. Свободные члены ограничений составляют крайний левый столбец таблицы. Слева от таблицы записаны текущие базисные переменные (X1,..., Xm). Сверху от таблицы приведен набор всех переменных задачи, где Xm+1,..., Xn - свободные переменные задачи.

Преобразования таблицы надо производить до тех пор, пока не будет получена симплекс-таблица, которая одновременно является прямо и двойственно допустимой.

Данный метод получил широкое распространение и большую популярность по сравнению с другими подходами, так как крайне редко на практике встречаются задачи трудные для симплекс-метода.

Геометрический метод

Применяется дя задач с двумя переменными. Метод решения состоит в следующем:

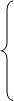На плоскости Ох1х2 строятся прямые, которые задают соответствующие ограничения:

a11 x1 + a11 x2 + …… + a11 xn = b1,

a21 x1 + a22 x2 + …… + a2n xn = b2,

…………………………………………

am1 x1 + am2 x2 + …… + amn xn = bm.

Находим множество всех точек х1,х2, удовлетворяющим всем неравенствам. Такое множество называется областью допустимых решений. Строим вектор и перемещаем линию уровня, который задается уравнением: с1х1+с2х2 = const в направлении вектора до последней точки пересечения с ОДР. Эта точка и дает решение задачи Lmax = значению L в этой точки

Двойственная задача.

Общая схема построения двойственной задачи.

Если задана общая задача ЛП:

где D определяется системой уравнений и неравенств:

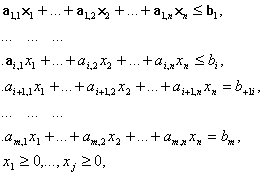
то двойственной по отношению к ней называется общая задача ЛП:

где D* определяется системой уравнений и неравенств:

Как следует из приведенной схемы при переходе от прямой задачи ЛП к двойственной:

1. Тип оптимума меняется на противоположный, т. е. максимум на минимум, и наоборот.

2. Вектор коэффициентов целевой функции c и столбец ограничений b меняются местами.

3. Матрица ограничений задачи А транспонируется.

4. Множество индексов переменных, на которые наложено условие неотрицательности в прямой задаче определяют номера ограничений, имеющих форму неравенств в двойственной задаче.

5. Множество номеров ограничений, имеющих форму неравенств в прямой задаче определяют множество индексов переменных, на которые накладывается условие неотрицательности, в двойственной задаче.

Из приведенного определения вытекает важное свойство — симметричность отношения двойственности, т. е. задача, двойственная по отношению к двойственной, совпадает с прямой (исходной) задачей.

((D*)*, (f*)*)≡(D, f),

Основные теоремы:

Теорема 1. Если одна из двойственных задач имеет конечный оптимум, то другая также имеет конечный оптимум, причем экстремальные значения целевых функций совпадают

Теорема 2 (о дополняющей нежесткости). Для того чтобы план х* и у* являлись оптимальными решениями соответственно задач линейного программирования и двойственной к ним необходимо и достаточно, чтобы выполнялись следующие соотношения:

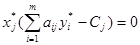
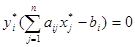
Теорема 3 (об оценках). Значение переменных 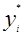в оптимальном решении двойственной задачи представляет собой оценки влияния свободных членов bi в системе ограничения прямой задачи на величину целевой функции f(x*)

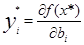
Транспортная задача.

Одна из наиболее распространенных задач математического программирования — транспортная задача. В общем виде ее можно представить так: требуется найти такой план доставки грузов от поставщиков к потребителям, чтобы стоимость перевозки (или суммарная дальность, или объем транспортной работы в тонно-километрах) была наименьшей. Следовательно, дело сводится к наиболее рациональному прикреплению производителей к потребителям продукции (и наоборот). В простейшем виде, когда распределяется один вид продукта и потребителям безразлично, от кого из поставщиков его получать, задача формулируется следующим образом.

Имеется ряд пунктов производства с объемами производства в единицу времени (месяц, квартал), равными соответственно и пункты потребления потребляющие за тот же промежуток времени соответственно 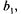продукции. В случае, если решается закрытая (сбалансированная) задача, сумма объемов производства на всех пунктах-поставщиках равна сумме объемов потребления на всех пунктах-получателях:

Кроме того, известны затраты по перевозке единицы продукта от каждого поставщика к каждому получателю — эти величины обозначаются 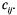В качестве неизвестных величин выступают объемы продукта, перевозимого из каждого пункта производства в каждый пункт потребления, соответственно обозначаемые .

Тогда наиболее рациональным прикреплением поставщиков к потребителям будет такое, при котором суммарные затраты на транспортировку будут наименьшими:

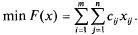
При этом каждый потребитель получает нужное количество продукта:

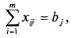
и каждый поставщик отгружает весь произведенный им продукт:

Как и во всех подобных случаях, здесь также оговаривается неотрицательность переменных: поставка от какого-то пункта производства тому или иному пункту потребления может быть равна нулю, но отрицательной, т. е. следовать в обратном направлении, быть не может.

Рассмотрим таблицу.

Строки транспортной таблицы соответствуют пунктам производства (в последней клетке каждой строки указан объем запаса продукта ai), а столбцы — пунктам потребления (последняя клетка каждого столбца содержит значение потребности bj). Все клетки таблицы (кроме тех, которые расположены в нижней строке и правом столбце) содержат информацию о перевозке из i-го пункта в j-й: в левом верхнем углу находится цена перевозки единицы продукта, а в правом нижнем — значение объема перевозимого груза для данных пунктов. Клетки, которые содержат нулевые перевозки (xi,j=0), называют свободными, а ненулевые — занятыми (xi,j>0).

	В1	В2	……	Вn	Всего
	C_1,1	C_1,2	……	C_1,n	а1
A₁	C_2,1	C_2,2	……	C_2,n	а2
A₂	….	….	….	….
….	…	…	…	….	….
A_m	C_m,1	C_m,2	……	C_m,n	аm
	b1	b2		bn

Несбалансированную (открытую) транспортную задачу приводят к виду, показанному выше, искусственно: в модель вводятся так называемые фиктивный поставщик или фиктивный потребитель, которые балансируют спрос и потребление.

В настоящее время разработано множество различных алгоритмов решения транспортной задачи: распределительный метод, метод потенциалов, дельта-метод, венгерский метод, метод дифференциальных рент, различные сетевые методы и т. д.

123 4 5

Воспользуйтесь поиском по сайту: