Особенности машинной арифметики, точность вычислений на ЭВМ

ВВЕДЕНИЕ

Цикл лабораторных работ предназначен для студентов второго курса (четвертый семестр), изучающих дисциплину "Вычислительная математика" и работающих в компьютерных классах на базе ЭВМ типа IBM PC AT-286 и выше, снабженных компилятором языка С (С++). Первые две работы цикла посвящены особенностям машинной арифметики, точности вычислений на ЭВМ и обусловленности вычислительной задачи. Они служат практической иллюстрацией вводной части теоретического курса дисциплины. Каждая из последующих работ ставит целью изучение либо конкретного численного метода, либо набора численных процедур (схем, формул), позволяющих реализовать выполнение одной из классических задач вычислительной математики: решение нелинейных уравнений, интерполирование функций, численное интегрирование, решение систем линейных алгебраических уравнений. Порядок расположения лабораторных работ в методических указаниях соответствует последовательности изложения лекционного материала. Для углубленного изучения перечисленных выше задач и методов их решения целесообразно воспользоваться литературой [1-10], приведенной в библиографическом списке.

Выполнение каждой лабораторной работы следует осуществлять поэтапно в следующем порядке:

- подготовка к решению задачи на персональной ЭВМ (ПЭВМ);

- проведение вычислительного эксперимента на ПЭВМ;

- анализ результатов вычислений; оформление отчета.

Подготовка к решению задачи на ПЭВМ производится как вне компьютерного класса, так и непосредственно на ПЭВМ. Она включает:

- ознакомление с описанием работы и заданием для выполнения;

- составление программных модулей, содержащих определенные заданием и персональным вариантом вычислительной процедуры, и/или ввод исходных данных;

- компиляцию разработанных программных модулей, их отладку и сопряжение с имеющимся для большинства работ программами-функциями, реализующими конкретные численные методы;

- планирование вычислительного эксперимента на ПЭВМ в рамках выполняемого задания.

Программы - функции, предназначенные для применения в процессе вычислений, представлены в виде библиотеки модулей на языке программирования С++. Это предопределяет ориентацию цикла работ на студентов, владеющих данным языком и навыками программирования в необходимом объеме.

Проведение вычислительного эксперимента на ПЭВМ осуществляется в соответствии с порядком выполнения работы и заданием на исследование указанных зависимостей и обусловленности изучаемого метода.

Анализ результатов вычислений заключается в построении исследуемых зависимостей и сравнительной оценке метода (вычислительной процедуры) по характерным для данной группы методов параметрам, например, скорости сходимости, степени обусловленности, достижимой точности и т.п.

Анализ результатов и оформление отчета производится вне компьютерного класса.

Отчет должен содержать:

- постановку задачи;

- тексты разработанных программ;

- результаты вычислений, их теоретический и экспериментальный анализ в виде таблиц и графиков, снабженных необходимыми комментариями;

- развернутые выводы по лабораторной работе.

В методических указаниях приведено также задание на курсовую работу, которая ориентирована на исследование четырех методов решения нелинейных уравнений.

 

Особенности машинной арифметики, точность вычислений на ЭВМ

(Лабораторная работа №1)

 

В фундаменте математического анализа прочно утвердилась система действительных чисел. Однако, как бы она не упрощала анализ, практические вычисления вынуждены обходиться без нее [9].

Обычным способом аппроксимации системы действительных чисел в ЭВМ посредством конкретных математических представлений являются числа с плавающей точкой. Множество F чисел с плавающей точкой характеризуется четырьмя параметрами: основанием b, точностью t и интервалом показателей [L,M]. Каждое число 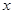с плавающей точкой, принадлежащее F, имеет значение

,

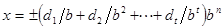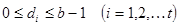где целые числа удовлетворяют неравенствам и 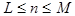. Если для каждого ненулевого 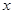из F справедливо , то система F называется нормализованной. Целое число 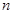называется показателем, а число 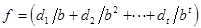- дробной частью. Обычно целое число 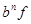хранится по той или иной схеме представления, принятой для целых чисел, например, величины со знаком, дополнения до единицы или дополнения до двух. Если принять 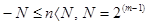, то переходим к общепринятой терминологии, при которой t - разрядность мантиссы, m - разрядность порядка.

Действительная машинная реализация представлений чисел с плавающей точкой может отличатся в деталях от рассматриваемой идеальной, однако различия несущественны, и на практике их почти всегда можно игнорировать, анализируя основные проблемы ошибок округления. Величина b^1-t является оценкой относительной точности плавающей арифметики, которая характеризуется посредством машинного эпсилон, т.е. наименьшего числа с плавающей точкой e, такого, что 1+e>1. Точное значение машинного эпсилон зависит не только то указанных выше параметров, но и от принятого способа округления.

В вычислительных машинах используются различные системы чисел с плавающей точкой, причем в некоторых ЭВМ несколько систем. Так, для современных ПЭВМ характерно применение двух систем, которые называются обычной точностью и удвоенной точностью.

Рассматриваемое множество F не является континуумом или даже бесконечным множеством. Оно содержит ровно 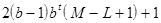чисел, которые расположены неравномерно (равномерность расположения имеет место лишь при фиксированном показателе). В силу того, что F - конечное множество, не представляется возможным сколь-нибудь детально отобразить континуум действительных чисел. Например, действительные числа модулей, большим максимального элемента из F, вообще не могут быть отображены, причем последнее справедливо также в отношении ненулевых действительных чисел, меньших по абсолютной величине по сравнению с наименьшим положительным числом из F, и, наконец, каждое число из F должно представлять целый интервал действительных чисел, для которой, как и для любой модели, присущи допущения и ограничения.

На множестве F определены арифметические операции в соответствии с тем, как они выполняются ЭВМ. Эти операции, в свою очередь моделируются в машине посредством приближений, называемых плавающими операциями. Для плавающих операций сложения, вычитания, умножения и деления существует возможность возникновения ошибок округления, переполнения и появления машинного нуля. Следует отметить, что операции плавающего сложения и умножения коммутативны, но не ассоциативны, и дистрибутивный закон для них также не выполняется. Невыполнение указанных алгебраических законов, имеющих фундаментальное значение для математического анализа, приводит к сложности анализа плавающих вычислений и возникающих при этом ошибок.

Целью лабораторной работы №1 является изучение особенностей вычислений с плавающей точкой.

В работе предлагается, используя готовые программы, выполнить исследования машинной арифметики и точности вычислений на ПЭВМ. Программы для удобства пользователя объединены в одном исполняемом модуле lab1.exe, запускаемом на выполнение просто указанием имени и нажатием клавиши "Enter". В модуле приведены аннотация к лабораторной работе, развернутые теоретические пояснения к каждому заданию (программе), собственно задания и рекомендации по вариации значений параметров при проведении расчетов. Программы в процессе работы выдают подсказки по действиям пользователя и запросы на ввод значений параметров. Это позволяет студентам осуществлять многосторонние исследования, одновременно усваивая теоретические положения вводной части курса дисциплины "Вычислительная математика".

Работа в соответствии с числом используемых расчетных программ содержит следующие четыре задания:

1) исследуйте распределение нормализованных чисел с плавающей точкой на вещественной оси для различных значений параметров b, t, m (из-за ограниченности ресурсов ПЭВМ не рекомендуется задавать большие значения параметров: b=2, t£7, m£4);

2) вычислите значения величины машинного эпсилон e(с) для различных значений константы c, меняющихся от 0 до 2¹⁵, постройте график этой зависимости и объясните полученные результаты;

3) исследуйте абсолютные и относительные ошибки округления при вычислениях с плавающей точкой сумм чисел (N чисел вида 1/N) при различных значениях шага суммирования;

4) исследуйте проявления ошибок округления, возникающих при вычислении показательной функции e^x для чисел с плавающей точкой для двух вариантов алгоритма вычислений, также скорость сходимости обоих вариантов.

В последнем задании при первом варианте алгоритма значение функции e^x вычисляется как сумма сходящегося бесконечного ряда, а при втором число x разлагается на целую и дробную части [9].

Студентам требуется выполнить все перечисленные задания, при этом индивидуальных вариантов не предусматривается, - значения необходимых параметров выбираются по усмотрению каждого исследователя. Порядок выполнения заданий может быть произвольным, однако рекомендуется придерживаться приведенной в их перечислении последовательности 1),2),3),4).

 

 

12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: