 |
Решение нелинейных уравнений
|
|
|
|
Задача нахождения корней нелинейных уравнений вида  (где
(где  - некоторая непрерывная функция) встречается в различных областях инженерной и научной деятельности [1-10]. Нелинейные уравнения делятся на два класса - алгебраические и трансцендентные. Алгебраическими называются уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). Уравнения, которые содержат другие функции (тригонометрические, показательные, логарифмические и т.п.), называются трансцендентными.
- некоторая непрерывная функция) встречается в различных областях инженерной и научной деятельности [1-10]. Нелинейные уравнения делятся на два класса - алгебраические и трансцендентные. Алгебраическими называются уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). Уравнения, которые содержат другие функции (тригонометрические, показательные, логарифмические и т.п.), называются трансцендентными.
Методы решения нелинейных уравнений подразделяются на прямые и итерационные. Прямые методы позволяют записать корни в виде некоторого конечного соотношения. Такие методы для решения ряда трансцендентных, а также простейших алгебраических уравнений известны из школьного курса алгебры. Однако встречающиеся на практике уравнения не удается решить столь простыми методами. Для их решения применяются итерационные методы, при которых алгоритм нахождения корня уравнения в общем случае включает два этапа:
- отыскания приближенного значения корня или содержащего его отрезка;
- уточнения приближенного значения до некоторой заданной степени точности.
Общие сведения
Пусть задана непрерывная функция  вещественного аргумента x и требуется численным методом решить уравнение
вещественного аргумента x и требуется численным методом решить уравнение  , т.е. найти приближение x* к вещественному корню этого уравнения. Если уравнение имеет несколько вещественных корней, то сначала производят их отделение (изоляцию), а затем уточняют положение отдельного корня. Считается, что отделение корня произведено, если выделен такой интервал [a0, b0] области определения функции
, т.е. найти приближение x* к вещественному корню этого уравнения. Если уравнение имеет несколько вещественных корней, то сначала производят их отделение (изоляцию), а затем уточняют положение отдельного корня. Считается, что отделение корня произведено, если выделен такой интервал [a0, b0] области определения функции  , на концах которого значения функции
, на концах которого значения функции  (a0) и
(a0) и  (b0) имеют разные знаки и внутри которого имеется ровно один корень уравнения
(b0) имеют разные знаки и внутри которого имеется ровно один корень уравнения  . Для уточнения метода используют итерационные методы, такие как метод бисекции (половинного деления), метод хорд (секущих или ложного положения), метод Ньютона (касательных), метод итераций (последовательных приближений). В указанных методах вычисляются либо последовательность значений границ сужающихся интервалов a0, b0, a1, b1,..., an, bn,..., содержащих корень, либо последовательность приближений к корню x0, x1, x2,..., xn,...[2,7,8,11].
. Для уточнения метода используют итерационные методы, такие как метод бисекции (половинного деления), метод хорд (секущих или ложного положения), метод Ньютона (касательных), метод итераций (последовательных приближений). В указанных методах вычисляются либо последовательность значений границ сужающихся интервалов a0, b0, a1, b1,..., an, bn,..., содержащих корень, либо последовательность приближений к корню x0, x1, x2,..., xn,...[2,7,8,11].
|
|
|
В первом случае итерационный процесс заканчивается, как только длина текущего интервала становится достаточно малой (например, ½bn-an½<e). Во втором случае условием остановки вычислений является малость очередного приращения hn=xn-xn-1, ½hn½<e. В обоих случаях параметр e определяет момент остановки вычислений. Иногда в качестве условия остановки используют условие ½  (
(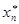 ) ½<e, где
) ½<e, где 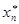 - текущее приближение к корню, например,
- текущее приближение к корню, например, 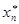 =1/2(an + bn ) в методе бисекции. Выполнение этого условия свидетельствует о малости значения функции в точке
=1/2(an + bn ) в методе бисекции. Выполнение этого условия свидетельствует о малости значения функции в точке 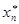 , т.е. позволяет считать, что
, т.е. позволяет считать, что  (
(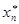 )»0.
)»0.
Для каждого итерационного метода можно указать некоторые условия сходимости. Однако не всегда легко проверить или гарантировать выполнение этих условий. Кроме того необходимо учесть особенности машинных вычислений при реализации итерационных методов. На практике эти затруднения обходят, вводя ограничение nmax на число итераций. Такое ограничение предохраняет от "зацикливания" метода, а также позволяет выявить практическое отсутствие сходимости вычислительного процесса.
Целью лабораторных работ, приводимых в данном разделе, является изучение перечисленных выше четырех итерационных методов приближенного решения нелинейных уравнений, при этом каждая работа посвящена одному из них. Для выполнения работ предлагается использовать набор программ - функций, реализующих конкретные численные методы, а также программу - функцию Round, позволяющую моделировать ошибки в исходных данных. Указанные программы (язык C) размещаются в директории LIBR1.
|
|
|
Метод бисекции
(Лабораторная работа №3)
Если найден отрезок [a,b], такой, что  (a)
(a)  (b)<0, существует точка c, в которой значение функции равно нулю, т.е.
(b)<0, существует точка c, в которой значение функции равно нулю, т.е.  (с)=0, сÎ(a,b). Метод бисекции состоит в построении последовательности вложенных друг в друга отрезков, на концах которых функция имеет разные знаки. Каждый последующий отрезок получается делением пополам предыдущего. Процесс построения последовательности отрезков позволяет найти нуль функции
(с)=0, сÎ(a,b). Метод бисекции состоит в построении последовательности вложенных друг в друга отрезков, на концах которых функция имеет разные знаки. Каждый последующий отрезок получается делением пополам предыдущего. Процесс построения последовательности отрезков позволяет найти нуль функции  (корень уравнения
(корень уравнения  с любой заданной точностью.
с любой заданной точностью.
Рассмотрим один шаг итерационного процесса. Пусть на (n-1)-м шаге найден отрезок [an-1, bn-1]Ì[a, b], такой, что  (an-1)
(an-1)  (bn-1)<0. Разделим его пополам точкой x=(an-1 +bn-1)/2 и вычислим
(bn-1)<0. Разделим его пополам точкой x=(an-1 +bn-1)/2 и вычислим  (x). Если
(x). Если  (x)=0, то x=(an-1+bn-1)/2- корень уравнения. Если
(x)=0, то x=(an-1+bn-1)/2- корень уравнения. Если  (x)¹0, то из двух половин отрезка выбирается та, на концах которой функция имеет противоположные знаки, поскольку искомый корень лежит на этой половине, т.е.
(x)¹0, то из двух половин отрезка выбирается та, на концах которой функция имеет противоположные знаки, поскольку искомый корень лежит на этой половине, т.е.
an=an-1, bn=x, если  (x)
(x)  (an-1) < 0;
(an-1) < 0;
an=x, bn= bn-1, если  (x)
(x)  (an-1) > 0.
(an-1) > 0.
Если требуется найти корень с точностью e, то деление пополам продолжается до тех пор, пока длина отрезка не станет меньше 2e. Тогда координата середины отрезка есть значение корня с требуемой точностью e.
Метод бисекции является простым и надежным методом поиска простого корня уравнения  (простым называется корень x=c дифференцируемой функции
(простым называется корень x=c дифференцируемой функции  , если
, если  (с) и
(с) и 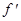 (с)¹0). Этот метод сходится для любых непрерывных функций
(с)¹0). Этот метод сходится для любых непрерывных функций  , в том числе недифференцируемых. Скорость его сходимости невысока. Для достижения точности e необходимо совершить N»log2(b-a)/e итераций. Это означает, что для получения каждых трех верных десятичных знаков необходимо совершить около 10 итераций.
, в том числе недифференцируемых. Скорость его сходимости невысока. Для достижения точности e необходимо совершить N»log2(b-a)/e итераций. Это означает, что для получения каждых трех верных десятичных знаков необходимо совершить около 10 итераций.
В лабораторной работе №3 предлагается, используя программы - функции BISECT и Round из файла methods.cpp (файл заголовков metods.h, директория LIBR1), найти корень уравнения  методом бисекции с заданной точностью Eps, исследовать зависимость числа итераций от точности Eps при изменении Eps от 0.1 до 0.000001, исследовать обусловленность метода (чувствительность к ошибкам в исходных данных).
методом бисекции с заданной точностью Eps, исследовать зависимость числа итераций от точности Eps при изменении Eps от 0.1 до 0.000001, исследовать обусловленность метода (чувствительность к ошибкам в исходных данных).
Выполнение работы осуществляется по индивидуальным вариантам заданий (нелинейных уравнений), приведенным в подразделе 3.6. Номер варианта для каждого студента определяется преподавателем.
|
|
|
Порядок выполнения работы должен быть следующим:
1) Графически или аналитически отделить корень уравнения  (т.е. найти отрезки [Left, Right], на которых функция
(т.е. найти отрезки [Left, Right], на которых функция  удовлетворяет условиям теоремы Коши).
удовлетворяет условиям теоремы Коши).
2) Составить подпрограмму вычисления функции  .
.
3) Составить головную программу, содержащую обращение к подпрограмме f(x), BISECT, Round и индикацию результатов.
4) Провести вычисления по программе. Построить график зависимости числа итераций от Eps.
5) Исследовать чувствительность метода к ошибкам в исходных данных. Ошибки в исходных данных моделировать с использованием программы Round, округляющей значения функции с заданной точностью Delta.
Текст программы-функции BISECT, предназначенной для решения уравнения  методом бисекции, представлен в подразделе 3.7.
методом бисекции, представлен в подразделе 3.7.
Метод хорд
(Лабораторная работа №4)
Пусть найден отрезок [a, b], на котором функция  меняет знак. Для определенности положим
меняет знак. Для определенности положим  (a)>0,
(a)>0,  (b)<0. В методе хорд процесс итераций состоит в том, что в качестве приближений к корню уравнения
(b)<0. В методе хорд процесс итераций состоит в том, что в качестве приближений к корню уравнения  принимаются значения c0, c1,... точек пересечения хорды с осью абсцисс, как это показано на рис.1.
принимаются значения c0, c1,... точек пересечения хорды с осью абсцисс, как это показано на рис.1.

Сначала находится уравнение хорды АВ:
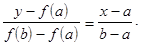
Для точки пересечения ее с осью абсцисс (x=c0, y=0) получается уравнение
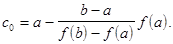
Далее сравниваются знаки величин  (a) и
(a) и  (с0) и для рассматриваемого случая оказывается, что корень находится в интервале (a, c0), так как
(с0) и для рассматриваемого случая оказывается, что корень находится в интервале (a, c0), так как  (a)
(a)  (с0)<0. Отрезок [c0,b] отбрасывается. Следующая итерации состоит в определении нового приближения c1 как точки пересечения хорды АВ1 с осью абсцисс и т.д. Итерационный процесс продолжается до тех пор, пока значение
(с0)<0. Отрезок [c0,b] отбрасывается. Следующая итерации состоит в определении нового приближения c1 как точки пересечения хорды АВ1 с осью абсцисс и т.д. Итерационный процесс продолжается до тех пор, пока значение  (cn) не станет по модулю меньше заданного числа e (см. подраздел 3.1).
(cn) не станет по модулю меньше заданного числа e (см. подраздел 3.1).
Алгоритмы методов бисекции и хорд похожи, однако метод хорд в ряде случаев дает более быструю сходимость итерационного процесса, причем успех его применения, как и метода бисекции, гарантирован.
В лабораторной работе №4 предлагается, используя программы - функции HORDA и Round из файла methods.cpp (файл заголовков metods.h, директория LIBR1), найти корень уравнения  с заданной точностью Eps методом хорд, исследовать скорость сходимости и обусловленности метода.
с заданной точностью Eps методом хорд, исследовать скорость сходимости и обусловленности метода.
|
|
|
Для данной работы, как и для лабораторной работы №3 задаются индивидуальные варианты нелинейных уравнений (см. подраздел 3.6).
Порядок выполнения лабораторной работы №4:
1) Графически или аналитически отделить корень уравнения  (т.е. найти отрезки [Left, Right], на которых функция
(т.е. найти отрезки [Left, Right], на которых функция  удовлетворяет условиям применимости метода).
удовлетворяет условиям применимости метода).
2) Составить подпрограмму - функцию вычисления функции  , предусмотрев округление значений функции с заданной точностью Delta с использованием программы Round.
, предусмотрев округление значений функции с заданной точностью Delta с использованием программы Round.
3) Составить головную программу, вычисляющую корень уравнения  и содержащую обращение к подпрограмме f(x), HORDA, Round и индикацию результатов.
и содержащую обращение к подпрограмме f(x), HORDA, Round и индикацию результатов.
4) Провести вычисления по программе. Теоретически и экспериментально исследовать скорость сходимости и обусловленность метода.
В подразделе 3.7 приводится текст программы - функции HORDA, предназначенной для решения уравнения  методом хорд.
методом хорд.
Метод Ньютона
(Лабораторная работа № 5)
В случае, когда известно хорошее начальное приближение решения уравнения  , эффективным методом повышения точности является метод Ньютона. Он состоит в построении итерационной последовательности
, эффективным методом повышения точности является метод Ньютона. Он состоит в построении итерационной последовательности  сходящейся к корню уравнения
сходящейся к корню уравнения  . Достаточные условия сходимости метода формулируются теоремой, приведенной в [1,7].
. Достаточные условия сходимости метода формулируются теоремой, приведенной в [1,7].
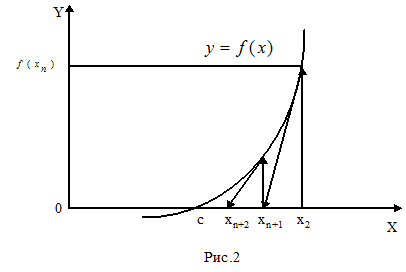
Метод Ньютона допускает простую геометрическую интерпретацию (рис. 2). Если через точку с координатами 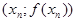 провести касательную, то абсцисса точки пересечения этой касательной с осью Ох будет очередным приближением xn+1 корня уравнения
провести касательную, то абсцисса точки пересечения этой касательной с осью Ох будет очередным приближением xn+1 корня уравнения  .
.
Для оценки погрешности n-го приближения корня предлагается пользоваться неравенством
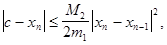
где М2-наибольшее значение модуля второй производной 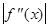 на отрезке [a,b]; m1-наименьшее значение модуля первой производной
на отрезке [a,b]; m1-наименьшее значение модуля первой производной 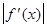 на отрезке [a,b]. Таким образом, если
на отрезке [a,b]. Таким образом, если 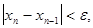 то
то  Это означает, что при хорошем начальном приближении корня после каждой итерации число верных десятичных знаков в очередном приближении удваивается, т.е. процесс сходится очень быстро (имеет место квадратическая сходимость). Из указанного следует, что при необходимости нахождения корня с точностью e итерационный процесс можно прекращать, когда
Это означает, что при хорошем начальном приближении корня после каждой итерации число верных десятичных знаков в очередном приближении удваивается, т.е. процесс сходится очень быстро (имеет место квадратическая сходимость). Из указанного следует, что при необходимости нахождения корня с точностью e итерационный процесс можно прекращать, когда
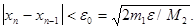 (3.1)
(3.1)
Рассмотрим один шаг итераций. Если на (n-1)-м шаге очередное приближение xn-1 не удовлетворяет условию окончания процесса, то вычисляются величины 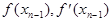 и следующие приближение корня
и следующие приближение корня 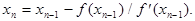 При выполнении условия (3.1) величина xn принимается за приближенное значение корня с, вычисленное с точностью e.
При выполнении условия (3.1) величина xn принимается за приближенное значение корня с, вычисленное с точностью e.
|
|
|
В лабораторной работе № 5 предлагается, используя программы-функции NEWTON и ROUND из файла methods.cpp (файл заголовков methods.h, директория LIBR1), найти корень уравнения  с заданной точностью Eps методом Ньютона, исследовать скорость сходимости и обусловленность метода.
с заданной точностью Eps методом Ньютона, исследовать скорость сходимости и обусловленность метода.
Для данной работы вид функции  задается индивидуально каждому студенту преподавателем из числа вариантов, приведенных в подразделе 3.6.
задается индивидуально каждому студенту преподавателем из числа вариантов, приведенных в подразделе 3.6.
Порядок выполнения лабораторной работы №5.
1) Графически или аналитически отделить корень уравнения  (т.е. найти отрезки [Left, Right], на котором функция
(т.е. найти отрезки [Left, Right], на котором функция  удовлетворяет условиям сходимости метода Ньютона).
удовлетворяет условиям сходимости метода Ньютона).
2) Составить подпрограммы - функции вычисления  ,
,  , предусмотрев округление их значений с заданной точностью Delta.
, предусмотрев округление их значений с заданной точностью Delta.
3) Составить головную программу, вычисляющую корень уравнения  и содержащую обращение к подпрограммам,
и содержащую обращение к подпрограммам,  ,
, 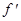 (x), Round, NEWTON и индикацию результатов.
(x), Round, NEWTON и индикацию результатов.
4) Выбрать начальное приближение корня x0 из [Left, Right] так, чтобы 
 >0.
>0.
5) Провести вычисления по программе. Исследовать скорость сходимости метода и чувствительность метода к ошибкам в исходных данных.
Для приближенного вычисления корней уравнения  методом Ньютона предназначена программа - функция NEWTON, текст которой представлен в подразделе 3.7.
методом Ньютона предназначена программа - функция NEWTON, текст которой представлен в подразделе 3.7.
Метод простых итераций
(Лабораторная работа №6)
Метод простых итераций решения уравнения  состоит в замене исходного уравнения эквивалентным ему уравнением x=j(x) и построении последовательности xn+1=j(xn), сходящейся при n®¥ к точному решению. Достаточные условия сходимости метода простых итераций формулируются теоремой, приведенной [1,2,7].
состоит в замене исходного уравнения эквивалентным ему уравнением x=j(x) и построении последовательности xn+1=j(xn), сходящейся при n®¥ к точному решению. Достаточные условия сходимости метода простых итераций формулируются теоремой, приведенной [1,2,7].
Рассмотрим один шаг итерационного процесса. Исходя из найденного на предыдущем шаге значения xn-1, вычисляется y= j(xn-1). Если 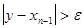 , то полагается xn=y и выполняется очередная итерация. Если же
, то полагается xn=y и выполняется очередная итерация. Если же  , то вычисления заканчиваются и за приближенное значение корня принимается величина xn=y. Погрешность результата вычислений зависит от знака производной
, то вычисления заканчиваются и за приближенное значение корня принимается величина xn=y. Погрешность результата вычислений зависит от знака производной 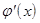 : при
: при 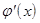 >0 погрешность определения корня составляет qe/1-q, а при
>0 погрешность определения корня составляет qe/1-q, а при 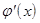 <0 погрешность не превышает e. Здесь q- число, такое, что ½
<0 погрешность не превышает e. Здесь q- число, такое, что ½ 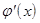 ½£q<1 на отрезке [a,b]. Существование числа q является условием сходимости метода в соответствии с отмеченной выше теоремой.
½£q<1 на отрезке [a,b]. Существование числа q является условием сходимости метода в соответствии с отмеченной выше теоремой.
Для применения метода простых итераций определяющее значение имеет выбор функции  в уравнении
в уравнении  , эквивалентном исходному. Функцию
, эквивалентном исходному. Функцию  необходимо подбирать так, чтобы ½
необходимо подбирать так, чтобы ½ 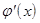 ½£q<1. Это обусловливается тем, что если
½£q<1. Это обусловливается тем, что если 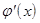 <0 на отрезке [a,b], то последовательные приближения xn=j(xn-1) будут колебаться около корня c, если же
<0 на отрезке [a,b], то последовательные приближения xn=j(xn-1) будут колебаться около корня c, если же 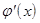 >0, то последовательные приближения будут сходиться к корню c монотонно. Следует также помнить, что скорость сходимости последовательности {xn} к корню c функции
>0, то последовательные приближения будут сходиться к корню c монотонно. Следует также помнить, что скорость сходимости последовательности {xn} к корню c функции  тем выше, чем выше число q.
тем выше, чем выше число q.
В лабораторной работе № 6 предлагается, используя программы-функции ITER и Round из файла methods.cpp (файл заголовков methods.h, директория LIBR1), найти корень уравнения  с заданной точностью Eps методом итераций, исследовать скорость сходимости и обусловленность метода.
с заданной точностью Eps методом итераций, исследовать скорость сходимости и обусловленность метода.
Для данной работы вид функции  задается индивидуально каждому студенту преподавателем из числа вариантов, приведенных в подразделе 3.6.
задается индивидуально каждому студенту преподавателем из числа вариантов, приведенных в подразделе 3.6.
Порядок выполнения лабораторной работы №6 должен быть следующим.
1) Графически или аналитически отделить корень уравнения  .
.
2) Преобразовать уравнение  к виду
к виду  так, чтобы в некоторой окрестности [Left, Right] корня производная
так, чтобы в некоторой окрестности [Left, Right] корня производная 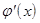 удовлетворяла условию ½
удовлетворяла условию ½ 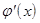 ½£q<1. При этом следует иметь в виду, что чем меньше величина q, тем быстрее последовательные приближения сходятся к корню.
½£q<1. При этом следует иметь в виду, что чем меньше величина q, тем быстрее последовательные приближения сходятся к корню.
3) Выбрать начальное приближение, лежащее на [Left, Right].
4) Составить подпрограмму для вычисления значений 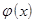 ,
, 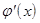 , предусмотрев округление вычисленных значений с точностью Delta.
, предусмотрев округление вычисленных значений с точностью Delta.
5) Составить головную программу, вычисляющую корень уравнения и содержащую обращение к программам 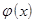 ,
, 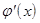 и ITER и индикацию результатов.
и ITER и индикацию результатов.
6) Провести вычисления по программе. Исследовать скорость сходимости и обусловленность метода.
Текст программы - функции ITER, позволяющей вычислять корни уравнения x= 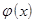 для любой функции, которая удовлетворяет достаточным условиям сходимости метода, приводится ниже.
для любой функции, которая удовлетворяет достаточным условиям сходимости метода, приводится ниже.
3.6. Курсовая работа по дисциплине и варианты заданий
Лабораторные работы, описанные в настоящем разделе, целесообразно объединять для выполнения курсовой работы, нацеленной на сравнительную оценку различных методов приближенного решения нелинейных уравнений. Типовое задание на курсовую работу формулируется следующим образом.
Задание на курсовую работу по дисциплине "Вычислительная математика".
Используя программы - функции BISECT, NEWTON, HORDA, ITER, Round из файла methods.cpp (файл заголовков methods.h, директория LIBR1), найти корень уравнения  с заданной точностью методом бисекции, Ньютона, хорд и итераций соответственно.
с заданной точностью методом бисекции, Ньютона, хорд и итераций соответственно.
Исследуйте обусловленность методов и зависимость числа итераций от точности результата Eps при изменении Eps от 0.0 до 0.000001.
Порядок выполнения курсовой работы
Графически или аналитически отделить корень уравнения  (т.е. найти отрезки [Left, Right], на которых функция
(т.е. найти отрезки [Left, Right], на которых функция  удовлетворяет условиям применимости методов).
удовлетворяет условиям применимости методов).
Составить подпрограмму- функцию вычисления функции  и ее производной
и ее производной  (при необходимости), предусмотрев округление их значений с заданной точностью Delta с использованием библиотечной функции Round.
(при необходимости), предусмотрев округление их значений с заданной точностью Delta с использованием библиотечной функции Round.
Составить головную программу, содержащую ввод исходных данных, обращение к подпрограммам BISECT, NEWTON, HORDA, ITER вывод результатов.
Выполнить вычисления по программе. Построить графики зависимости числа итераций, необходимых для достижения заданной точности Eps, от величины Eps, а также достижимой точности результатов от точности Delta задания функции  .
.
Теоретически и экспериментально сравнить методы бисекции, Ньютона, хорд и итераций по скорости сходимости и степени обусловленности.
Результаты оформить в виде отчета, содержащего постановку задачи, тексты разработанных программ, результаты теоретического и экспериментального анализа в виде таблиц и графиков, выводы.
Вид функции  определяется вариантом задания. Эти же варианты могут использоваться при выполнении лабораторных работ №№3-6 по отдельности.
определяется вариантом задания. Эти же варианты могут использоваться при выполнении лабораторных работ №№3-6 по отдельности.
| № п/п | 
| № п/п | 
|
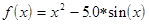 ; ;
| 
| ||
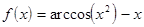 ; ;
| 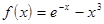 ; ;
| ||
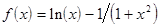 ; ;
| 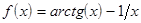 ; ;
| ||
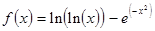 ; ;
|  ; ;
| ||
 ; ;
| 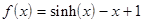 ; ;
| ||
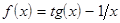 ; ;
| 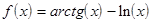 ; ;
| ||
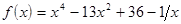 ; ;
| 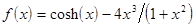 ; ;
| ||
 ; ;
|  ; ;
| ||
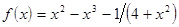 ; ;
| 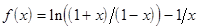 ; ;
| ||
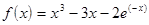 ; ;
| 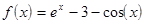 ; ;
| ||
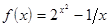 ; ;
|  ; ;
| ||
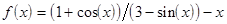 ; ;
| 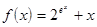 ; ;
| ||
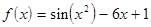 ; ;
| 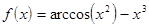 ; ;
| ||
 ; ;
|  ; ;
| ||
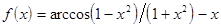 ; ;
| 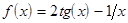 ; ;
| ||
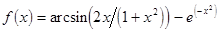 ; ;
| 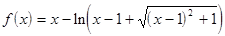 ; ;
| ||
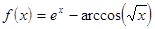 ; ;
|  ; ;
| ||
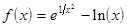 ; ;
| 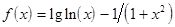 ; ;
|
|
|
|


