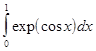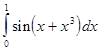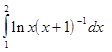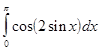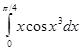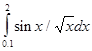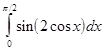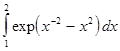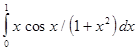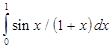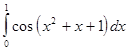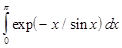 |
Формула Гаусса. (Лабораторная работа №7)
|
|
|
|
В квадратурной формуле Гаусса
узлы 
и коэффициенты 
подобраны так, чтобы формула была точна для всех многочленов степени 
. Для приближенного вычисления интеграла по конечному отрезку 
выполняется замена переменной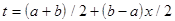 
; тогда квадратурная формула Гаусса принимает вид [2,8,12]
Таблица 4.1
|
,
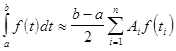где 
; 
- узлы квадратурной формулы Гаусса; 
- гауссовы коэффициенты 
.
Если подынтегральная функция достаточно гладкая, то формула Гаусса обеспечивает очень высокую точность при небольшом числе узлов.
В лабораторной работе №7 требуется, используя квадратурную формулу Гаусса наивысшего порядка точности, вычислить приближенное значение заданного интеграла.
Интеграл предлагается вычислить по квадратурной формуле Гаусса с восемью узлами:
, 
;
, 
;
, 
;
, 
.
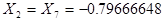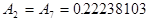Порядок выполнения лабораторной работы №7.
1) Составить программу-функцию для вычисления интеграла по формуле Гаусса.
2) Составить программу-функцию для вычисления значений подынтегральной функции.
3) Составить головную программу, содержащую обращение к вычислительным процедурам и осуществляющую печать результатов.
4) Результаты работы оформить в виде краткого отчета, содержащего характеристику используемого метода вычислений, его точности и полученное значение интеграла.
Варианты заданий к лабораторной работе приведены в таблице 4.2.
Библиографический список
1. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров: Уч.пособие.- М.: Высш.шк., 1994. - 544 с.
|
|
|
2. Бахвалов Н.С., Жидков Н.О., Кобельков Г.М. Численные методы. - М.: Наука, 1987. - 600 с.
3. Березин И.С., Жидков Н.П. Методы вычислений. Т.1.- М.: Наука, 1966. - 632.
4. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Наука, 1970. - 664 с.
5. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. - М.: Наука, 1972. - 367 с.
6. Марчук Г.И. Методы вычислительной математики. - М.: Наука, 1989. - 608 с.
7. Плис А.И., Сливина Н.А. Лабораторный практикум по высшей математики: Учеб. Пособие для втузов. - 2-е изд. - М.: Высш.шк., 1994. - 416 с.
8. Самарский А.А., Гулин А.В. Численные методы. - М.: Наука, 1989. - 432 с.
9. Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений/Пер. с англ. - М.: Мир, 1980. - 279 с.
10. Хемминг Р. Численные методы/Пер. с англ. - М.: Наука, 1972. - 400 с.
11. Сборник задач по структурному программированию: Учеб. пособие/С.А. Ивановский, Ю.Е. Прокофьев, А.В. Смольянинов / Под ред. В.И. Тимохина. - Л.: ЛЭТИ, 1987. - 64 с.
12. Воробьева Г.Н., Данилова А.Н. Практикум по численным методам. - М.: Высш.шк, 1979. - 184 с.
13. Волков Е.А. Численные методы: Учеб. пособие. - М.: Наука, 1982. - 256 с.
14. Основы математического моделирования. Построение и анализ моделей с примерами на языке MATLAB: Учеб. пособие/ Д.Л. Егоренков, А.Л. Фрадков, В.Ю. Харламов; Под ред. А.Л. Фрадкова. - С.-Пб.: БГТУ, 1994. - 192 с.
15. Компьютерная математика. Методич. указ. к лаборат. работам/Сост. И.А. Назаров. - С.-Пб.: ГЭТУ, 1993. - 32 с.
Таблица 4.2
|
Содержание
ÂÂÅÄÅÍÈÅ...................................................................................................................................................................................................
1. ÎÑÎÁÅÍÍÎÑÒÈ ÌÀØÈÍÍÎÉ ÀÐÈÔÌÅÒÈÊÈ, ÒÎ×ÍÎÑÒÜ ÂÛ×ÈÑËÅÍÈÉ ÍÀ ÝÂÌ............................................................................
|
|
|
(Ëàáîðàòîðíàÿ ðàáîòà ¹1)................................................................................................................................................................
2. ÈÇÓ×ÅÍÈÅ ÏÎÍßÒÈß ÎÁÓÑËÎÂËÅÍÍÎÑÒÈ ÂÛ×ÈÑËÈÒÅËÜÍÎÉ ÇÀÄÀ×È.................................................................................
(Ëàáîðàòîðíàÿ ðàáîòà ¹2)...............................................................................................................................................................
3. ÐÅØÅÍÈÅ ÍÅËÈÍÅÉÍÛÕ ÓÐÀÂÍÅÍÈÉ............................................................................................................................................
3.1. Îáùèå ñâåäåíèÿ..........................................................................................................................................................................
3.2. Ìåòîä áèñåêöèè...........................................................................................................................................................................
(Ëàáîðàòîðíàÿ ðàáîòà ¹3)..............................................................................................................................................................
3.3. Ìåòîä õîðä.......................................................................................................................................................................................
(Ëàáîðàòîðíàÿ ðàáîòà ¹4)..............................................................................................................................................................
3.4. Ìåòîä Íüþòîíà.................................................................................................................................................................................
(Ëàáîðàòîðíàÿ ðàáîòà ¹ 5).............................................................................................................................................................
3.5. Ìåòîä ïðîñòûõ èòåðàöèé.......................................................................................................................................................
|
|
|
(Ëàáîðàòîðíàÿ ðàáîòà ¹6)..............................................................................................................................................................
3.6. Êóðñîâàÿ ðàáîòà ïî äèñöèïëèíå è âàðèàíòû çàäàíèé.........................................................................................
3.7. Ïðîãðàììû äëÿ ðåøåíèÿ íåëèíåéíûõ óðàâíåíèé.........................................................................................................
4. ×ÈÑËÅÍÍÎÅ ÈÍÒÅÃÐÈÐÎÂÀÍÈÅ.......................................................................................................................................................
4.1. Ñîñòàâíûå ôîðìóëû ïðÿìîóãîëüíèêîâ, òðàïåöèé, Ñèìïñîíà..................................................................................
(Ëàáîðàòîðíàÿ ðàáîòà ¹6)..............................................................................................................................................................
4.2. Ôîðìóëà Ãàóññà. (Ëàáîðàòîðíàÿ ðàáîòà ¹7)...............................................................................................................
Áèáëèîãðàôè÷åñêèé ñïèñîê........................................................................................................................................................
|
|
|
