Статистические характеристики погрешностей навигационной информации

Навигационная информация, получаемая от любого датчика, представляет собой случайную функцию, для большинства датчиков стационарную. Ошибки навигационной информации наиболее пол­но характеризуются их автокорреляционной функцией или спект­ральной плотностью. Автокорреляционная функция стационарного случайного процесса показывает изменение степени стохастической связи ошибок в зависимости от изменения интервала между изме­рениями. Функция спектральной плотности стационарного случай­ного процесса описывает распределение дисперсии этого процесса по частотам. Функция спектральной плотности стационарного слу­чайного процесса и его автокорреляционная функция связаны меж­ду собой прямым и обратным преобразованиями Фурье.

Для большинства датчиков навигационной информации авто­корреляционная функция погрешности имеет вид (рис. 184)

 

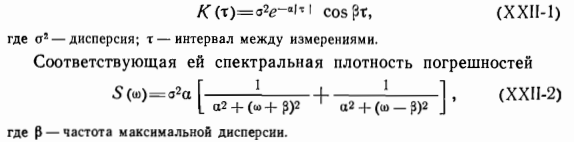
§ 70. СПОСОБЫ ОБЪЕДИНЕНИЯ НАВИГАЦИОННОЕ ИНФОРМАЦИИ

Физический смысл комплек- сирования и условия, от кото­рых зависит его эффективность, хорошо иллюстрируются при­мерами схем компенсации и фильтрации.

Схема компенсации (рис. 185). Обозначим навигацион­ную информацию, поступаю­щую от первого датчика,

где U1 — измеренное значение нави­гационного параметра; U — истинное значение навигационного параметра; Д| — погрешность измерений первого датчика.

Аналогично информация от второго датчика = Фильтр

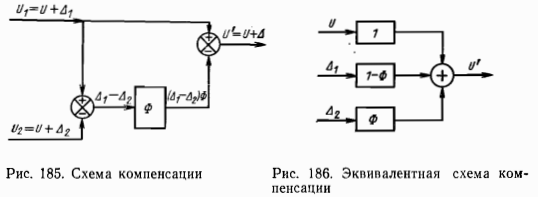
Ф стремятся сконструировать так, чтобы он не пропускал погреш­ность второго датчика Д₂ и в минимальной степени искажал по­грешность первого датчика Дь Если бы удалось создать идеальный фильтр, который полностью отфильтровал бы погрешность Д₂, не искажая при этом погрешности Ai, то на выходе схемы компенса­ции было бы истинное значение навигационного параметра U. В реальном фильтре часть погрешности Д₂ просочится на его вы­ход и несколько изменится погрешность А\. Поэтому выходной сиг­нал схемы компенсации кроме истинного значения навигационного параметра будет содержать некоторую погрешность А:

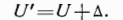
Найдем погрешность Д на выходе схемы компенсации. Напря­жение с выхода первого вычитающего устройства, поступающее на вход фильтра Ф, представляет собой разность погрешностей пер­вого и второго датчиков:

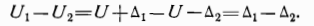
Так как сигнал на выходе фильтра (Ai—Аг)Ф, то сигнал после вто­рого вычитающего устройства (на выходе схемы компенсации):

Выражение (XXII—5) определяет эквивалентную схему, пока­занную на рис. 186. Из эквивалентной схемы видно, что сигнал, проходя через схему компенсации, не изменяется, а погрешности А? и Л] претерпевают те же изменения, которые произошли бы, если бы они прошли через два взаимно-обратных фильтра соответствен­но |Ф| и |1—Ф|. Рассмотрим, как эти преобразования влияют на погрешности измерений, для чего определим изменения спектраль­ной плотности погрешностей Ai и Д₂ при прохождении через филь­тры |Ф| и 11—Ф|.

Из теории случайных функций известна зависимость между дисперсией и спектральной плотностью

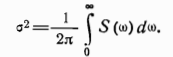
Дисперсии погрешностей первого и второго датчиков соответствен­но:

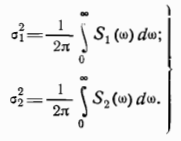
Спектральная плотность сигнала на выходе фильтра равна про­изведению спектральной плотности сигнала на входе фильтра на квадрат нормированной амплитудно-частотной характеристики этого фильтра:

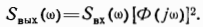
Тогда спектральные плотности погрешностей датчиков после фильтров будут:

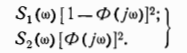
Следовательно, дислерсия погрешности на выходе схемы компен­сации

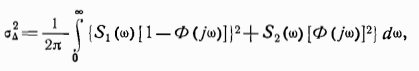
где S, и S ₂(ω) —спектральные плотности погрешностей датчиков навигационной инфор­мации; Ф (fω)—нормированная амплитудно- частотная характеристика фильтра.

Формула позволяет, зная спектральные плотности погрешностей навигационных датчиков и амплитуд­но-частотную характеристику фильтра, оценить величину погрешности на вы­ходе фильтра.

Если спектры погрешностей источ­ников навигационной информации рас­положены в разных частотных облас­тях, средняя квадратическая погрешность после комплексирования будет существенно меньше, чем у каждой из комплексируемых сис­тем в отдельности. Результат при этом в значительной мере зави­сит от качества фильтра.

 

Лучшая оценка навигационного парамет­ра по критерию минимума средней квадратической погрешности бу­дет при применении фильтра, называемого оптимальным. В настоя­щее время оптимальную фильтрацию осуществляют не аппаратур­ным, а программным путем, используя входящую в состав комп­лекса ЭВМ. В качестве оптимальных фильтров в этом случае ис­пользуют преимущественно фильтры Калмана, представляющие собой рекуррентный метод оценки состояний случайного процесса.

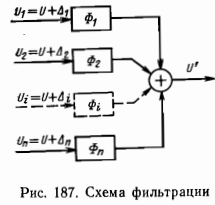Схема фильтрации (рис. 187). Из рисунка видно, что сигнал на выходе схемы фильтрации

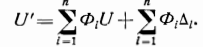
Выражение показывает, что для того, чтобы комп­лексная система не имела динамических ошибок, то есть не иска­жала полезный сигнал, должно быть выполнено условие

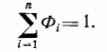
Вместе с тем из условия видна невозможность по­строения устройства, сглаживающего информацию одного источни­ка и не вносящего при этом искажений в полезный сигнал. Умень­шение случайных погрешностей без искажения полезного сигнала возможно, когда имеется минимум два источника информации. Ес­ли схему фильтрации использовать для объединения информации двух источников, то из выражения видно, что характе­ристики фильтров должны быть |Ф| и |1—Ф |. Схема фильтрации в этом случае даст тот же результат, что и схема компенсации, но в ней будет два фильтра вместо одного.

 

Рис. 187. Схема фильтрации

Наибольший эффект дает комплексирование автономных си­стем (систем счисления из курсоуказателя и измерителя скорости или инерциальиых систем) с неавтономными, например радиотех­ническими, так как спектры их погрешностей лежат в разных ча­стотных областях. Однако такие системы относятся к навигацион­ным комплексам, и вопросы их построения выходят за рамки курса радионавигации.

В последнее время появилась тенденция комплексирования раз­нородных радионавигационных средств, в частности приемоинди- каторов фазовых и импульсно-фазовых систем, с спутниковой судо­вой навигационной аппаратурой.

§ 71. КОМПЛЕКСНОЕ ИСПОЛЬЗОВАНИЕ хуя

 

хуя

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: