 |
Дифференциальные уравнения
|
|
|
|
3.7.1 Дифференциальные уравнения 1-го порядка.
3.7.2 Задача Коши. Теорема существования и единственности.
3.7.3 Линейные дифференциальные уравнения второго и третьего порядков.
3.7.4 Теорема об общем решении ЛОДУ. ЛОДУ II-го порядка с постоянными коэффициентами. Структура общего решения.
3.7.5 Линейные неоднородные дифференциальные уравнения II-го порядка с постоянными коэффициентами.
3.7.6 Системы дифференциальных уравнений.
Теория вероятностей
3.8.1 Элементы комбинаторики.
3.8.2 Случайные события.
3.8.3 Классическое определение вероятности.
3.8.4 Алгебра событий. Теоремы сложения и умножения вероятностей.
3.8.5 Теорема полной вероятности. Формула Бейеса.
3.8.6 Формула Бернулли. Локальная и интегральная теоремы Лапласа. Теорема Пуассона.
3.8.7 Дискретные случайные величины. Законы распределения. Числовые характеристики дискретных случайных величин.
3.8.8 Непрерывные случайные величины. Функция распределения и плотность распределения вероятностей. Числовые характеристики непрерывных случайных величин.
3.8.9 Нормальное и равномерное распределения.
Элементы математической статистики
3.9.1 Генеральная совокупность и выборка. Статистическое распределение выборки.
3.9.2 Эмпирическая функция распределения.
3.9.3 Полигон и гистограмма.
3.9.4 Точечные оценки. Выборочная средняя и выборочная дисперсия. Исправленная выборочная дисперсия.
3.9.5 Интервальные оценки. Точность оценки. Доверительная вероятность и доверительный интервал.
3.9.6 Проверка статистических гипотез. Критерий Пирсона.
3.9.7 Выборочное уравнение регрессии. Линейная регрессия.
3.9.8 Выборочный коэффициент корреляции.
3.9.9 Построение выборочного уравнения линейной регрессии.
|
|
|
Варианты контрольных заданий
Студент должен выполнять контрольные задания по номеру варианта, который совпадает с последней цифрой его учебного номера (шифра).
| № варианта | Тема №1 | Тема №2 | Тема №3 |
| 111, 121, 131 | 211, 221, 231 | 311, 321 | |
| 112, 122, 132 | 212, 222, 232 | 312, 322 | |
| 113, 123, 133 | 213, 223, 233 | 313, 323 | |
| 114, 124, 134 | 214, 224, 234 | 314, 324 | |
| 115, 125, 135 | 215, 225, 235 | 315, 325 | |
| 116, 126, 136 | 216, 226, 236 | 316, 326 | |
| 117, 127, 137 | 217, 227, 237 | 317, 327 | |
| 118, 128, 138 | 218, 228, 238 | 318, 328 | |
| 119, 129, 139 | 219, 229, 239 | 319, 329 | |
| 1110, 1210, 1310 | 2110, 2210, 2310 | 3110, 3210 |
| № варианта | Тема №4 | Тема №5 | Тема №6 |
| 411, 421, 431, 441 | 511, 521 | 611, 621, 631, 641 | |
| 412, 422, 432, 442 | 512, 522 | 612, 622, 632, 642 | |
| 413, 423, 433, 443 | 513, 523 | 613, 623, 633, 643 | |
| 414, 424, 434, 444 | 514, 524 | 614, 624, 634, 644 | |
| 415, 425, 435, 445 | 515, 525 | 615, 625, 635, 645 | |
| 416, 426, 436, 446 | 516, 526 | 616, 626, 636, 646 | |
| 417, 427, 437, 447 | 517, 527 | 617, 627, 637, 647 | |
| 418, 428, 438, 448 | 518, 528 | 618, 628, 638, 648 | |
| 419, 429, 439, 449 | 519, 5429 | 619, 629, 639, 649 | |
| 4110, 4210, 4310, 4410 | 5110, 5210 | 6110, 6210, 6310, 6410 |
| № варианта | Тема №7 | Тема №8 | Тема №9 |
| 711, 721, 731, 741 | 811, 821, 831, 841 | 911, 921, 931 | |
| 712, 722, 732, 742 | 812, 822, 832, 842 | 912, 922, 932 | |
| 713, 723, 733, 743 | 813, 823, 833, 843 | 913, 923, 933 | |
| 714, 724, 734, 744 | 814, 824, 834, 844 | 914, 924, 934 | |
| 715, 725, 735, 745 | 815, 825, 835, 845 | 915, 925, 935 | |
| 716, 726, 736, 746 | 816, 826, 836, 846 | 916, 926, 936 | |
| 717, 727, 737, 747 | 817, 827, 837, 847 | 917, 927, 937 | |
| 718, 728, 738, 748 | 818, 828, 838, 848 | 918, 928, 938 | |
| 719, 729, 739, 749 | 819, 829, 839, 849 | 919, 929, 939 | |
| 7110, 7210,7310, 7410 | 8110, 8210, 8310, 8410 | 9110, 9210, 9310 |
| № варианта | Тема №10 | Тема №11 | Тема №12 |
| 1011, 1021, 1031, 1041 | 1111, 1121, 1131 | 1211, 1221 | |
| 1012, 1022, 1032, 1042 | 1112, 1122, 1132 | 1212, 1222 | |
| 1013, 1023, 1033, 1043 | 1113, 1123, 1133 | 1213, 1223 | |
| 1014, 1024, 1034, 1044 | 1114, 1124, 1134 | 1214, 1224 | |
| 1015, 1025, 1035, 1045 | 1115, 1125, 1135 | 1215, 1225 | |
| 1016, 1026, 1036, 1046 | 1116, 1126, 1136 | 1216, 1226 | |
| 1017, 1027, 1037, 1047 | 1117, 1127, 1137 | 1217, 1227 | |
| 1018, 1028, 1038, 1048 | 1118, 1128, 1138 | 1218, 1228 | |
| 1019, 1029, 1039, 1049 | 1119, 1129, 1139 | 1219, 1229 | |
| 10110, 10210, 10310, 10410 | 11110, 11210, 11310 | 12110, 12210 |
Контрольные задания
Тема №1
|
|
|
Линейная алгебра
Задание 1.1 Вычислить определитель матрицы С.
1.1.1 
1.1.2 
1.1.3 
1.1.4 
1.1.5 
1.1.6 
1.1.7 
1.1.8 
1.1.9 
1.1.10 
Задание 1.2 Решить систему линейных уравнений
a) методом Крамера;
b) методом Гаусса.
1.2.1 
1.2.2 
1.2.3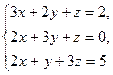 
1.2.4 
1.2.5 
1.2.6 
1.2.7 
1.2.8 
1.2.9 
1.2.10 
Задание 1.3 Решить систему методом Гаусса или доказать, что она несовместна. Если система имеет бесчисленное множество решений, найти общее и одно частное решения.
1.3.1 
1.3.2 
1.3.3 
1.3.4 
1.3.5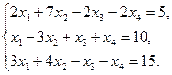 
1.3.6 
1.3.7 
1.3.8 
1.3.9 
1.3.10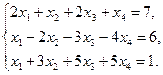 
Тема №2
Элементы векторной алгебры и аналитической геометрии
Задание 2.1 Даны уравнения двух прямых 
, 
и координаты точки 
Требуется найти:
а) уравнение прямой, проходящей через точку 
и точку пересечения данных прямых;
б) расстояние между точкой пересечения двух прямых и точкой ;
в) угол между прямыми и ;
г) уравнение прямой, проходящей через точку параллельно прямой ;
д) уравнение прямой, проходящей через точку перпендикулярно прямой ;
е) расстояние от точки до прямой .
ж) выполнить чертеж.
Выбрать оптимальные пути решения в пунктах б), в), г), д), е).
2.1.1 
2.1.2 
2.1.3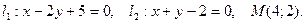 
2.1.4 
2.1.5 
2.1.6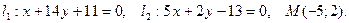 
2.1.7 
2.1.8 
2.1.9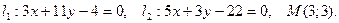 
2.1.10 
Задание 2.2 Даны координаты вершин пирамиды 
Найти:
а) длину ребра 
;
б) угол между ребрами и 
;
в) угол между ребрами и гранью 
;
г) площадь грани ;
д) объем пирамиды;
е) уравнение плоскости ;
ж) уравнение высоты, опущенной из вершины 
на грань .
з) сделать чертеж.
Выбрать оптимальные пути решения в пунктах б), в), г), д).
2.2.1 
2.2.2 
2.2.3 
2.2.4 
2.2.5 
2.2.6 
2.2.7 
2.2.8 
2.2.9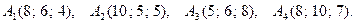 
2.2.10 
Задание 2.3 Привести уравнения кривых второго порядка к каноническому виду, назвать их и выполнить чертеж.
2.3.1
a)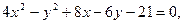 
b) 
c) 
2.3.2
a) 
b) 
c) 
2.3.3
a) 
b) 
c) 
2.3.4
a) 
b)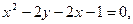 
c) 
2.3.5
a) 
b) 
c)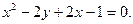 
2.3.6
a) 
b)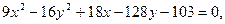 
c) 
2.3.7
a) 
b)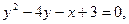 
c) 
2.3.8
a) 
b) 
c) 
2.3.9
a) 
b)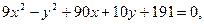 
c) 
2.3.10
a) 
b) 
c) 
Тема №3
Пределы и непрерывность функций
Задание 3.1 Вычислить пределы функций.
3.1.1
а) 
б) 
в) 
г) 
д) 
3.1.2
а) 
б)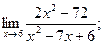 
в) 
г) 
д) 
3.1.3
а) 
б) 
в) 
г) 
д) 
3.1.4
а) 
б) 
в) 
г) 
д) 
3.1.5
а) 
б) 
в) 
г)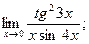 
д) 
3.1.6
а) 
б) 
в) 
г) 
д) 
3.1.7
а) 
б) 
в) 
г) 
д) 
3.1.8
а)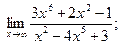 
б) 
в)
г) 
д) 
3.1.9
а) 
б) 
в) 
г) 
д) 
3.1.10
а) 
б)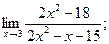 
в)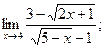 
|
|
|
г)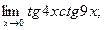 
д)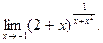 
Задание 3.2 Исследовать функции на непрерывность: найти точки разрыва, указать характер разрыва. Сделать схематический чертёж.
3.2.1
a) 
b) 
c) 
3.2.2
a) 
b) 
c) 
3.2.3
a) 
b) 
c) 
3.2.4
a) 
b) 
c) 
3.2.5
a) 
b)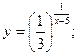 
c) 
3.2.6
a) 
b)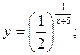 
c) 
3.2.7
a) 
b) 
c) 
3.2.8
a) 
b) 
c) 
3.2.9
a) 
b) 
c) 
3.2.10
a) 
b) 
c) 
Тема №4
Дифференцирование
Задание 4.1 Найти производные функций.
4.1.1
а)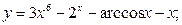 
б) 
в) 
г) 
4.1.2
а) 
б) 
в)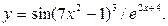 
г) 
4.1.3
а) 
б) 
в) 
г) 
4.1.4
а) 
б) 
в)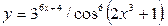 
г) 
4.1.5
а) 
б) 
в) 
г) 
4.1.6
а) 
б) 
в)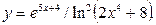 
г) 
4.1.7
а) 
б)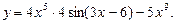 
в) 
г) 
4.1.8
а) 
б) 
в) 
г) 
4.1.9
а) 
б) 
в) 
г) 
4.1.10
а) 
б) 
в) 
г) 
Задание 4.2 Найти производные неявной и параметрической функций.
4.2.1
а) 
б) 
4.2.2
а) 
б)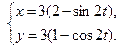 
4.2.3
а) 
б) 
4.2.4
а) 
б) 
4.2.5
а) 
б) 
4.2.6
а) 
б) 
4.2.7
а)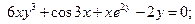 
б) 
4.2.8
а) 
б) 
4.2.9
а) 
б) 
4.2.10
а) 
б) 
Задание № 4.3 Найти предел функции с помощью правила Лопиталя или эквивалентных бесконечно малых.
Решение о выборе метода принять самостоятельно.
4.3.1 
4.3.2 
4.3.3 
4.3.4 
4.3.5 
4.3.6 
4.3.7 
4.3.8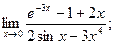 
4.3.9 
4.3.10 
Задание 4.4 Составить уравнения касательной и нормали к кривой в точке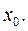 
Выполнить чертёж.
4.4.1 
4.4.2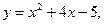 
4.4.3 
4.4.4 
4.4.5 
4.4.6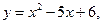 
4.4.7 
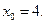
4.4.8 
4.4.9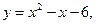 
4.4.10 
Тема №5
Исследование функций
Задание 5.1 Найти наибольшее и наименьшее значения функции 
на отрезке 
.
5.1.1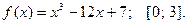 
5.1.2 
5.1.3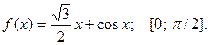 
5.1.4 
5.1.5 
5.1.6 
5.1.7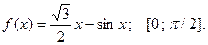 
5.1.8 
5.1.9 
5.1.10 
Задание 5.2 Исследовать методами дифференциального исчисления функции и построить их графики.
5.2.1
a) 
b) 
5.2.2
a) 
b) 
5.2.3
a) 
b) 
5.2.4
a)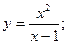 
b) 
5.2.5
a)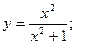 
b) 
5.2.6
a) 
b) 
5.2.7
a) 
b) 
5.2.8
a) 
b) 
5.2.9
a) 
b) 
5.2.10
a) 
b) 
Тема №6
Функции нескольких переменных
Задание 6.1 Найти частные производные:
а) первого порядка;
b) второго порядка.
6.1.1
a) 
;
b) 
.
6.1.2
a) 
;
b) 
.
6.1.3
a) 
;
b) 
.
6.1.4
a) 
;
b) 
.
6.1.5
a)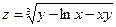 
;
b) 
.
6.1.6
a) 
;
b) 
.
6.1.7
a) 
;
b) 
.
6.1.8
a) 
;
b) 
.
6.1.9
a) 
;
b) 
.
6.1.10
a) 
;
b)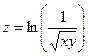 
.
Задание 6.2 Для заданной поверхности составить уравнения касательной плоскости и нормали в точке М(x0,y0,z0).
|
|
|
6.2.1. 
, М(2; -3; 1).
6.2.2. 
, М(2; 3; 4).
6.2.3. 
, М(2; 0; -2).
6.2.4. 
, М(4; 1; -2).
6.2.5. 
, М(-1; 2; 6).
6.2.6. 
, М(4; 1; -4).
6.2.7. 
, М(0; 2; 3).
6.2.8. 
, М(2; -3; 2).
6.2.9. 
, М(1; 2; -1).
6.2.10. 
, М(2; -3; 1).
Задание 6.3 Исследовать функцию на экстремум.
6.3.1 
.
6.3.2 
.
6.3.3 
.
6.3.4 
.
6.3.5 
.
6.3.6 
.
6.3.7 
.
6.3.8 
.
6.3.9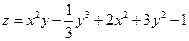 
.
6.3.10 
.
Задание 6.4 Для функции 
найти градиент и производную по направлению 
в точке 
.
6.4.1 
, 
6.4.2 
, 
6.4.3 
. 
6.4.4 
, 
6.4.5 
, 
6.4.6 
, 
6.4.7 
, 
6.4.8 
, 
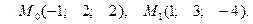
6.4.9 
, 
6.4.10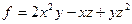 
, 
Тема №7
Неопределённые и определённые интегралы
Задание 7.1 Вычислить неопределённые интегралы.
7.1.1
a) 
;
b) 
;
c)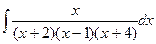 
.
7.1.2
a) 
;
b) 
;
c) 
.
7.1.3
a) 
;
b) 
;
c) 
.
7.1.4
a) 
;
b) 
;
c) 
.
7.1.5
a) 
;
b) 
;
c) 
.
7.1.6
a) 
;
b)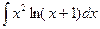 
;
c) 
.
7.1.7
a) 
;
b) 
;
c) 
.
7.1.8
a) 
;
b) 
;
c) 
.
7.1.9
a) 
;
b) 
;
c)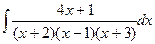 
.
7.1.10
a) 
;
b) 
;
c) 
.
Задание 7.2 Вычислить определенные интегралы (в пункте b) использовать универсальную тригонометрическую подстановку 
).
7.2.1
a) 
;
b) 
.
7.2.2
a) 
;
b) 
.
7.2.3
a) 
;
b) 
.
7.2.4
a) 
;
b) 
.
7.2.5
a) 
;
b)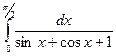 
.
7.2.6
a) 
;
b) 
.
7.2.7
a) 
;
b) 
.
7.2.8
a) 
;
b) 
.
7.2.9
a) 
;
b) 
.
7.2.10
a)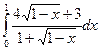 
;
b) 
.
Задание 7.3 Вычислить площадь фигуры, ограниченной данными линиями: а) в декартовых координатах; б) в полярных координатах.
7.3.1
a) 
, 
;
b) 
.
7.3.2
a) 
, 
;
b) 
.
7.3.3
a) 
; 
;
b) 
.
7.3.4
a) 
, 
, 
;
b) 
.
7.3.5
a) 
, 
;
b) 
.
7.3.6
a) 
, 
, 
.
b)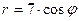 
.
7.3.7
a)
