 |
Аналогия формулы для расчёта работы
|
|
|
|
| № п/п | Раздел физики | Пример | Условие | Формула |
| Механика (динамика) | 
| FS = const FS = var |
A = FS . (S2 –S1)
A = 
| |
| Термодинамика | 
| Р = const Р = var |
A = Р . (V1 –V2)
A = 
| |
 3 3
| Электростатика | 
| q = const | A = q (φ1 – φ2) dA = qdφ |
| Электромагнетизм | 
| J = const | А = J (Ф1 – Ф2) dA = JdФ |
 |
Три вида магнетиков
| № п/п | Диамагнетики | Парамагнетики | Ферромагнетики | |
| Металлы | Си, Аq, Аи. | Аl, Pt | Fe, Ni, Co | |
| Суммарный магнитный момент электронов в атоме | 
 = 0 = 0
| 
 ≠ 0 (мал) ≠ 0 (мал)
| 
 ≠ 0 (велик) ≠ 0 (велик)
| |
Поведение во внешнем магнитном поле напряжённостью 
| 
| 
| 
| |
| Действие на величину внешнего магнитного поля | Чуть ослабляет | Чуть усиливает | Значительно усиливает | |
5 
| Магнитная проницательность среды μ |  μ = 0,999 μ = 0,999
|  μ = 1,001 μ = 1,001
|  μ =103 ÷ 106 μ =103 ÷ 106
|
| Магнитная восприимчивость χ = μ – 1 | χ = – 0,001 | χ = + 0,001 | χ = 103 ÷ 106 | |
Зависимость намагниченности среды Ј от напряжённости внешнего магнитного поля 
| 
| 
| 
| |
| Особенности поведения |   – –
| – | а) при Т ≥ Тк становится парамагнетиком б) при перемагничивании меняет линейные размеры |
Сравнение принципа устройства электродвигателя и электрогенератора
 |
| № п/п | Электродвигатель | Электрогенератор | |
 1 1
| Условие | На рамку в магнитном поле подаётся электрический ток J от внешнего источника | Рамка вращается в магнитном поле с угловой скоростью ω |
| Явление | Возникает вращающий момент сил М | Возникает переменная ЭДС индукции εi | |
| Закон | Ампера | Фарадея | |
| Расчёт | 
 FA = J.ℓ.B sin FA = J.ℓ.B sin  (для N = 1) (для N = 1)
| 
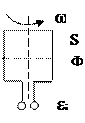 Ф = B. S. cos α (для N = 1) α = Ф = B. S. cos α (для N = 1) α = 
| |
| Пример | |||
| Результат | Рамка с током в магнитном поле сама вращается | В рамке, вращающейся в магнитном поле, появляется ток | |
| Превращение энергии | Электрическая в механическую | Механическая в электрическую | |
| Цель механизма | Совершить механическую работу за счёт энергии источника тока | Создать источник переменного тока за счёт механической энергии |

|
|
|
Три траектории движения электрического заряда в магнитном поле
| № п/п | Рисунок | Угол
α =  
| Синус угла Sin α | Скорость | Сила Лоренца | Траектория | Параметры траектории |

| α = 0 | Sin α = 0 | V = V|| | FЛ = q .V.B sin α FЛ = 0 | Прямая линия | Линия параллельная вектору индукции В | |

| 
| α = 90° | Sin α = 1 | V = V┴ | FЛ = q .V.B (max)
FЛ = Fц.с =  Направлена к центру (т.О)
Направлена к центру (т.О)
| Окружность | 

|

| 0 < α < 90° (острый) | 0 < sin α < 1 | 
 = V. sin α
V|| = V.cos α = V. sin α
V|| = V.cos α
| FЛ = q .V.B sin α | Винтовая линия | h = V|| .T |
 РАЗДЕЛ 6. КОЛЕБАНИЯ
РАЗДЕЛ 6. КОЛЕБАНИЯ
 6.1. Модель колебательного движения – проекция вращательного движения на плоскость
6.1. Модель колебательного движения – проекция вращательного движения на плоскость

Аналогия параметров вращательного и колебательного движения
| № п/п | Вращательное движение | Условие. Формула | Колебательное движение |
| X = R. sin φ | Х – смещение колеблющейся точки (м) | ||
| R = X max R – радиус вращения (м) | R = A = X max | A – амплитуда колебаний (м) | |
| φ – угол поворота (ρ) ∆ φ – угловой путь (ρ) | ∆ φ = 2πΝ Ν = 1 ∆ φ = 2π = 3600 | φ – фаза колебаний (ρ) φ0 – начальная фаза колебаний (ρ) |

Окончание таблицы
ω – угловая скорость  Связь угловой скорости и периода
Связь угла поворота и времени
Связь угловой скорости и периода
Связь угла поворота и времени
|  РМ вращение
РМ вращение  t0 = 0
t0 = 0 
 Ν = 1 φ = ωt +φ0
Ν = 1 φ = ωt +φ0
| ω – циклическая частота колебаний  Связь циклической частоты и периода
Зависимость фазы колебания от времени
Связь циклической частоты и периода
Зависимость фазы колебания от времени
| |
| Т – период вращения (с) | Ν = 1 Т = t1 об | Т – период колебаний (с) | |
 6 6
| ν – частота вращения  Связь частоты и периода
Связь угловой скорости и частоты
Уравнение гармонических колебаний
Связь частоты и периода
Связь угловой скорости и частоты
Уравнение гармонических колебаний
|  Ν = 1
Ν = 1 
 X = R sin φ = A sin (ωt + φ0)
X = R sin φ = A sin (ωt + φ0)
| Связь частоты и периода Связь двух частот Зависимость смещения от времени |
|
|
|
Аналогия формул кинематики поступательного движения и механических колебаний
Материальной точки с описанием электромагнитных колебаний в контуре
(Условия осуществления колебаний)
| № п/п | Поступательное движение | Механические колебания | Электромагнитные колебания | |||||
| Основной параметр | S – криволинейная координата (м) | х – смещение (м) | q – электрический заряд (Кл) | |||||
| Уравнение движения (колебаний) |  
|
|
|
Продолжение таблицы
| Мгновенная линейная скорость (сила тока) | 
|  
| 

| |||||
| Мгновенное линейное ускорение (ЭДС самоиндукции) |  
|  
|  
| |||||
| Связь параметров | – | 
| 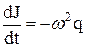
| |||||
 6 6
| Кинетическая энергия | 
| 
| 
| ||||
| Действующая сила | 
|
|
| |||||
| Коофифициент | k = 
| 
|   ; ; 
|
 |
Окончание таблицы
| Потенциальная энергия | 
| 
| 
| |||||
| Полная энергия | Е = Ек + Еn | 2.
| 2.
|

Сравнение механических колебаний пружинного и математического маятников
|
|
|
Воспользуйтесь поиском по сайту:

©2015 - 2026 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...







