С электромагнитными колебаниями в контуре

№ п/п	Маятники	Свободное состояние	Начальное отклонение	Возвращение в равновесие	Противоположное отклонение	Возвращение в равновесие	Исходное состояние
	Пружинный F упр = – kx	0 1 2 3 4 1
х = 0 Е = 0	х = х0 Еn = max V = 0 Ек = 0	х = 0 Еn = 0 V = max Ек = max	х = х0 Еn = max V = 0 Ек = 0	х = 0 Еn = 0 V = max Ек = max	х = х0 Еn = max V = 0 Ек = 0

Окончание таблицы

2	Математический	0   α = 0 Е = 0 положение равновесия	α = α0 Еn = max V = 0 Ек = 0	α = 0 Еn = 0 V = max Eк = max	α = α0 Еn = max V = 0 Е к = 0	α = 0 Еn = 0 V = max Eк = max	α = α0 Еn = max V = 0 Е к = 0
	Электромагнитный контур	q = 0 W = 0	q = q0 Wэ = max J = 0 Wм = 0 J >> εsi < 0 начальная зарядка	2     q = 0 Wэ = 0 J = max Wм = max J << εsi > 0 J >> εsi > 0 разрядка	q = 0 Wэ = max J = 0 Wм = 0 J >> εsi < 0 перезарядка	4     q = 00 Wэ = 0 J = max Wм = max J << εsi > 0 разрядка	q = q0 Wэ = max J = 0 Wм = 0 исходная зарядка

Расчёт частоты и периода незатухающих колебаний для пружинного, физического,

Математического маятников и колебательного контура

№ п/п	Маятник	Пружинный	Физический	Математический	Колебательный контур
1	Основной параметр
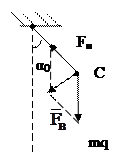
х – смещение (м)	α – угловое смещение (рад)	q – электрический заряд (Кл)
	Основной закон	II закон Ньютона для поступательного движения	II закон Ньютона для вращательного движения	II правило Кирхгофа для контура
	Силы (ЭДС)	F= – k x	M = – mgℓ . sin α	Uc= εsi = – Uc =
	Ускорение	a = x||	a = x||
	Дифференциальное уравнение ДУ І

Окончание таблицы

	ДУ ІІ
	Частота незатухающих колебаний			J = mℓ2
	Период незатухающих колебаний
	Коэффициент затухания	σ = 0	σ = 0	σ = 0	σ = 0
10	Решение ДУ
	Амплитуда колебаний	А0 = const	А0 = const	А0 = const	А0 = const
	Особенности		Тфм = Тм.м.

Сравнение незатухающих и затухающих механических и электромагнитных колебаний

 

№ п/п		Механические колебания пружинного маятника	Электромагнитные колебания в контуре
	Основной параметр	х – смещение	q – электрический заряд
	Основной закон	F = ma
	Сила (ЭДС)	незатухающие	затухающие	незатухающие	Затухающие
F = F упр = – k х	F = Fупр + Fсопр= – k х – rV
4	Ускорение	а = х||	V = х| а = V| = х||		J =
	Дифференциальное уравнение ДУ І
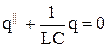
	ДУ ІІ
	Циклическая частота
	Период
	Коэффициент затухания	σ = 0		σ = 0
	Решение ДУ

Окончание таблицы

	Амплитуда	А0 = const		А0 = const
	Особенности
	Графики	а)	б)

 

 

 

 

 

а) незатухающий б) затухающий

 

 

Графики механического колебания пружинного маятника

 

 

Сравнение свободных и вынужденных электромагнитных колебаний

	Колебательный контур	Свободные коле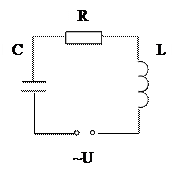бания	Вынужденные колебания
Незатухающие	Затухающие
	Внешний источник	нет	нет	Переменная ЭДС
3	Дифференциальные уравнения ДУ І ДУ ІІ			U= Um. sin (ωвt)
периодические	апериодические
	Сопротивление	R ≈0	R < R кр	R ≥ R кр	R – любое
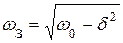	Циклическая частота		(δ<<)	(δ>>)
	Особенность
	Период			0 Т ∞

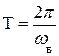
Окончание таблицы

	Решение ДУ			q = Aз
	Амплитуда	А0 = const
	График	а)	б)	в)	г)

 

10. График

 

 

а) б) в)

 

 

г)

Сравнение трёх элементов цепей переменного тока

 

	Резистор	Катушка	Конденсатор
Обозначение на схеме
Параметр	Сопротивление	Индуктивность	Ёмкость
Сопротивление	R – активное	ХL – реактивное индуктивное	ХС – реактивное ёмкостное
Зависимость сопротивления от частоты	не зависит R = const	прямопропорциональная ХL = ωt	обратно прямопропорциональная
Для постоянного тока (ω = 0)	R = const	ХL → 0	ХС → ∞
Векторная диаграмма
Направление вектора тока	совпадает по фазе с вектором напряжения	отстаёт от вектора напряжения на	опережает от вектора напряжения на

Последовательное и параллельное соединение элементов в цепях переменного тока

	Электрическая схема	U = Um.Sin (ωв.t)	U = Um.Sin (ωв.t)
2	Сила тока	JR = JL =JC = J	JR + JL + JC = J
	Напряжение	UR + UL + UC = U	UR = UL = UC = U
	Ось векторной диаграммы	Ось токов	Ось напряжений
	Векторная диаграмма		JCm – JLm
	Теорема Пифагора

 

Окончание таблицы

	Законы Ома	URm = Jm.R ULm = Jm.xL= JmωL	,
	Начальная фаза колебаний

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: