 |
Раздел 4. звукоизоляция. 4.1 Основные положения. 4.2. Звукоизоляция одинарной перегородки
|
|
|
|
Раздел 4. звукоизоляция
4. 1 Основные положения
Слово звукоизоляция обозначает два понятия - звукоизолирующая конструкция и физический эффект снижения шума.
С точки зрения звукоизолирующей конструкции звукоизоляция - это преграда, устанавливаемая на пути распространения звуковых волн, от которой происходит частичное отражение колебательной энергии обратно к источнику звука, уменьшая прохождение звука в защищаемое помещение или пространство. Для наиболее эффективного отражения звука волновое сопротивление конструкции должно как можно больше отличаться от волнового сопротивления среды, в которой распространяется звук. В таблице 4. 1 приведены плотности, скорости звука и волновые сопротивления воздуха и стали соответственно.
Таблица 4. 1
| Среда | Плотность r, кг/м3 | Скорость звука с, м/с | Волновое сопротивление rс, кг/м3с |
| Воздух Сталь | 1. 29 7. 8´ 103 | 340 5200 | 433 40. 6´ 106 |
Таким образом, стальная перегородка будет обладать хорошим звукоизолирующим эффектом для звука, распространяющегося в воздухе. Чем больше отражает поверхность, тем меньше звука проходит через нее. Так, гранитная стена настолько массивна и так мало сжимаема, что легкие молекулы воздуха не могут оказать на нее заметного воздействия. Плотность гранита велика, а вследствие его малой сжимаемости, скорость звука также велика. Поэтому волновое сопротивление гранита огромно. В результате этого при падении звуковой волны из воздуха на гранитную стенку отражается 99% падающей энергии (см. рис. 4. 1).
| Воздух |
| Воздух |
| Гранит |
| 100% |
| 99% |
| 1% |
| 1% |
| 0, 99% |
| 0, 01% |
| (r с)в> > (r с)u (r с)u> > (r с)в |
|
|
|
Рис. 4. 1. Прохождение энергии звуковой волны в воздухе через гранитную стенку
Однако 1% звуковой энергии входит в гранит и доходит до второй границы стены. Поскольку импеданс гранита велик, ничтожные смещения его частиц уже создают высокое давление в волне; однако, эти же смещения создают в воздухе весьма малое давление. Передача энергии снова будет мала.
При решении инженерных задач звукоизолирующие перегородки обычно изготовляют тонкими. Поскольку их толщина мала по сравнению с длиной волны, то обе их стороны движутся синфазно. В этом случае задача о распространении звука в материале перегородки перестает нас интересовать, и физика процесса приобретает другой характер.
4. 2. Звукоизоляция одинарной перегородки
Представим себе тонкую панель или перегородку площадью S м2, имеющую опору, но не закрепленную по периметру. Если с одной стороны приложить к ней постоянное давление, она прогнется и величина прогиба будет целиком определяться ее упругостью (жесткостью). Если давление на одну сторону будет медленно переходить от положительного к отрицательному, возникающее прогибание панели будет по прежнему определяться ее упругостью. Однако, поскольку перегородка обладает инерцией, при достаточном увеличении частоты знакопеременного давления, ее масса начнет сказываться в той же степени (а затем и больше), что и жесткость.
Поэтому говорят, что на очень низких частотах звукоизоляции перегородки управляется ее упругостью. По мере роста частоты все большую роль будет играть масса перегородки. Поясним это на примере, когда возбуждающая сила изменяется по гармоническому закону. В этом случае смещение перегородки синусоидально. На рис. 4. 2 показаны графики смещения, скорости и ускорения перегородки, колеблющейся на некоторой частоте, а также на частоте вдвое большей. При данном звуковом давлении с увеличением частоты смещение убывает по амплитуде, но скорость частиц остается без изменения (p=r с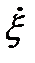 
, 
, 
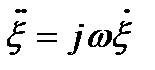). При этом, скорость изменения скорости стала вдвое больше: амплитуда ускорения удваивается при удвоении частоты. Но, согласно второму закону Ньютона, ускорение прямо пропорционально приложенной силе ( 
). Таким образом, теоретически при удвоении частоты потребовалась бы в двое большая сила, чтобы заставить перегородку колебаться с той же скоростью.
|
|
|
| y |
| t |
| t |
| t |
| y |
| t |
| t |
| t |
|
|
|
|
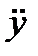
Рис. 4. 2. Изменение смещения, скорости, ускорения панели от времени
(при двух частотах колебаний, справа частота вдвое больше чем слева)
Однако, так как действующая со стороны звуковой волны сила не изменилась, удвоение частоты звука приведет к уменьшению амплитуды скорости колебаний у перегородки вдвое.
По другую сторону от панели картина такова, как если бы источником звука была панель (перегородка). Звук, падающий с одной стороны, приводит ее в колебания, и эти вынужденные колебания излучают с другой стороны звуковые волны - ослабленные копии падающих волн. Поскольку амплитуда скорости уменьшается вдвое при удвоении частоты, можно ожидать, что звуковое давление излучаемых с другой стороны волн также уменьшится вдвое, т. е. на 6дБ.
Как мы знаем из второго закона Ньютона, ускорение обратно пропорционально массе тела. Отсюда следует, что при данной частоте звукоизоляция перегородки увеличивается на 6дБ при каждом удвоении массы панели. Однако, это чисто теоретические рассуждения, на практике возникает множество обстоятельств, в результате которых поведение перегородки не следует точно этому " закону масс". Вместо улучшения изоляции на 6дБ удается получить не более 4-5дБ.
Перегородка как любая колебательная система обладает частотами собственных колебаний, которые определяются упругими и инерционными свойствами самой перегородки. Если частота падающей волны равна или близка к частоте собственных колебаний, то перегородка будет сильно раскачиваться под действием этой волны и эффективно передавать звук через перегородку. Этот резонанс напоминает резонанс груза на пружине, однако, по перегородке могут бежать изгибные волны, как это показано на рис. 4. 3. При наклонном падении звуковой волны на перегородку может оказаться, что длина волны звука, отсчитываемая вдоль перегородки, и длина изгибной волны на ней совпадают. В этом случае перегородка также начинает усиленно раскачиваться, что сопровождается весьма эффективной передачей звука с одной стороны на другую.
|
|
|
Рис. 4. 3. Эффект совпадений соответствует критической частоте ( 
)
Для данной длины изгибной волны существует такая частота падающего звука, ниже которой подобный " эффект совпадений" невозможен, так как даже при падении волны точно вдоль перегородки длина волны звука оказывается больше, чем длина изгибной волны. Эту частоту называют критической. Из всего сказанного следует, что перегородка, масса которой представляется достаточной, чтобы обеспечить хорошую изоляцию звука, на самом деле вследствие эффектов резонанса и совпадений оказывается почти бесполезной на целом ряде частот. Частотная зависимость звукоизоляции перегородки показана на рис. 4. 4. Из рисунка видно, что закон масс окажется выполненным лишь в некоторой полосе частот в середине спектра. Что же можно сделать? Один из способов расширить эту полосу частот, является сдвиг резонансных частот как можно больше вниз, а критическую частоту - как можно дальше вверх по частоте. Прежде всего, выясним, какую роль может сыграть упругость в осуществлении этой задачи. Чем податливей пружина, к которой прикреплена масса, тем ниже собственная частота.
Рис. 4. 4. Звукоизоляция одинарной перегородки: 1 - первый пространственный резонанс; 2 –закон масс; 3-резонанс совпадения (критическая или граничная частота)
Уменьшение жесткости перегородки не только понизит ее собственные частоты, но и укоротит изгибную волну, которая снижает изолирующие качества перегородки, и тем самым повысит критическую частоту. Более тонкая перегородка также имела бы более высокую критическую частоту, но при этом уменьшалась бы ее масса, что, как мы уже знаем, нежелательно.
|
|
|
Следующий прием - увеличение массы перегородки: это выгодно не только в силу закона масс, но и так же потому, что если это можно осуществить, не увеличивая жесткость перегородки, удастся также снизить резонансные частоты и поднять критическую частоту.
Существует, однако, и другой способ повышения звукоизоляции перегородки, и его можно использовать как независимо, так и совместно с вышеуказанными методами. Это демпфирование перегородки, которое существенно снизит потерю звукоизоляции в областях резонансов и эффекта совпадений (см. пунктирную линию на рис. 4. 4).
Теперь мы можем сформировать несколько положений, которыми необходимо руководствоваться при проектировании звукоизолирующих перегородок. Для всех частот, кроме самых низких, определяющими факторами являются:
а) большая масса; б) малая жесткость; в) высокое затухание.
Многие материалы сами по себе в той или иной степени обладают внутренним демпфированием. Например, внутреннее затухание в фанере велико - в сто раз больше, чем в стали. Однако при равных массах фанера обладает гораздо большей жесткостью, чем стальной лист. Поэтому при нанесении демпфирующего слоя стальной лист оказывается гораздо лучше фанеры, так как его резонансные частоты ниже, а критическая частота выше. Наилучшим материалом был бы свинец: его масса значительна, упругость мала, а затухание велико. Но свинец дорог. В таблице 4. 2 приведены сравнительные значения звукоизоляции различных перегородок.
Таблица 4. 2
| Звукоизоляция, дБ | ||||||||
| Материал перегородки | Толщина, мм | средняя | ||||||
| Гц | ||||||||
| Фанера | ||||||||
| Стекло | ||||||||
| Сталь | 1, 2 | |||||||
| Кирпич | ||||||||
| Бетон | ||||||||
| Патентованные модульные акустические панели | ||||||||
| Двойная перегородка из гипсовой штукатурки с металлическими связями | ||||||||
Для расчетной степени звукоизоляции запишем выражение для расчета коэффициента прохождения звука, падающего нормально на границу двух сред с различными волновыми сопротивлениями
(4. 1)
Волновое сопротивление воздушной среды
Z1=r c (4. 2)
Импеданс перегородки включает инерционное сопротивление на единицу ее площади и волновое сопротивление среды за стенкой, тогда для частотного диапазона действия " закона масс"
|
|
|
Z2 =jw m + r c (4. 3)
Подставляя (4. 2), (4. 3) в (4. 1) будем иметь
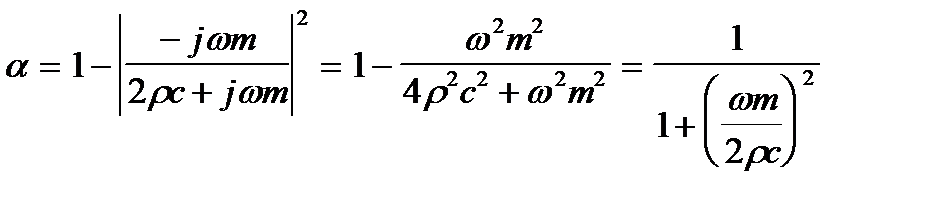(4. 4)
Введем понятие звукопроводности (коэффициент звукопередачи) конструкции t равной отношению энергии прошедшей через конструкцию к энергии, падающей на конструкцию. При отсутствии потерь t = a
Звукоизоляция перегородки при нормальном падении звука:
(4. 5)
при w m > > 1 (4. 5) можно упростить
(4. 6)
|
|
|
|
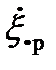
| Рпр |
| Рпад |
| Q |
| Q |
Рис. 4. 5. Прохождение звука через перегородку
При косом падении звука, звукоизоляция перегородки изменится (см. рис. 4. 5). Из условия
(4. 7)
где 
- нормальная составляющая колебательной скорости падающей волны, 
- нормальная составляющая колебательной скорости волны прошедшей через перегородку.
(4. 8)
Из (4. 8) импеданс перегородки при косом падении звука
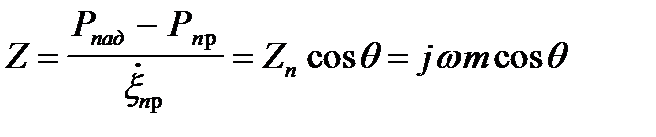(4. 9)
Аналогично выводу формулы (4. 4) можно получить
(4. 10)
Звукоизоляция перегородки при косом падении звука меньше, чем при нормальном падении. Явление уменьшения звукоизоляции при косом падении называется компонент - эффектом.
При расчете фундаментальных (т. е. самых низких собственных колебаний однослойных строительных преград) они могут быть рассмотрены как шарнирно опертые по краям тонкие пластины квадратной и прямоугольной формы, совершающие чисто изгибные колебания. Собственные частоты такой пластины определяют по формуле:
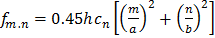, Гц (4. 10а)
где h - толщина пластины (преграды);
спр – скорость продольной волны в преграде:
μ – коэффициент Пуассона;
ρ – плотность среды;
a, b – размеры сторон пластины;
m, n – целочисленные значения, определяющие форму колебаний пластины (преграды).
|
|
|
