 |
Примеры решения задач. Задача 1. Найдем величину снижения уровня звукового давления до величины 0,2 от первоначального. Таким образом, уровень шума каждого из механизмов равен:
|
|
|
|
Примеры решения задач
Задача 1
В помещении установлены два механизма; каждый из них имеет уровень звукового давления над порогом 81 дБ. С помощью ряда мер звуковое давление каждого механизма снижено до величины 0, 2 от первоначального. Каков будет уровень шума в помещении?
Решение:
Найдем величину снижения уровня звукового давления до величины 0, 2 от первоначального.
Таким образом, уровень шума каждого из механизмов равен:
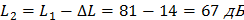
При удвоении силы звука (т. к. работающих механизмов два) звуковой уровень увеличивается на:
Следовательно, общий шум шума двух механизмов после принятия мер по обесшумливанию равен:
Ответ: 
Задача 2
Из условий задачи 1, определить при каком количестве работающих механизмов, уровень шума в помещении достигает 90 дБ?
Решение:
Суммарный уровень n источников шума:
По условию примера:
откуда
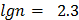и тогда: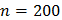 
Этот результат убеждает нас, насколько маловероятно получать в помещениях большие звуковые уровни при одновременной работе нескольких механизмов с малыми или средними уровнями шума. В условиях приведенного примера при доведении числа механизмов до 200 суммарный уровень шума практически не повысится до 90 дБ, так как для размещения такого большого числа механизмов потребуется сильно увеличить размеры помещения.
Ответ: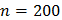
Задача 3
В помещении ограниченного объёма расположены пять механизмов. Уровни шума трех из них 80 дБ, уровень четвертого 83 дБ, пятого 77 дБ. Определить общий уровень шума.
Решение:
Рассчитаем уровень шума при работе трех источников одинакового уровня:
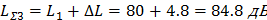
Для того, чтобы рассчитать уровень шума от двух источников разных уровней пользуются рисунком 3. 5 или выполняют расчет по формуле (3. 8).
|
|
|
Ответ: 
Задача 4
Частота основной составляющей шума трансформатора, определяющая общий уровень шума равна 100 Гц, уровень громкости её 100 фонов. На сколько надо понизить шум, чтобы уровень его громкости не превышал 70 фонов?
Решение:
По кривым равной громкости (рисунок 6. 1, приложения) находим, что на частоте 100 Гц уровню громкости в 100 фонов соответствует уровень звукового давления 104 дБ, а уровню громкости в 70 фонов – уровень звукового давления 76 дБ.
Следовательно, уровень силы звука надо снизить на 104-76=28 дБ. Как видно из таблицы 6. 2 приложения, это соответствует уменьшению звукового давления в 25 раз, а интенсивности звука в 630 раз.
Ответ: шум надо снизить на 28 дБ.
Задача 4
Анализ звука судового гудка и звука воздуходувки показал наличие в спектре этих звуков ряда тональных составляющих, определяющих общие уровни звуков. Уровни силы этих составляющих на расстоянии 5 м с указанием их частоты даны в соответствующих графах приведенной ниже таблицы. Определить, какой из звуков громче.
Решение:
По кривым равной громкости (рисунок 6. 1) определяем уровни громкости отдельных составляющих Li, затем по номограмме (рисунок 6. 3) их громкости Gi. Общую громкость находим суммированием громкостей отдельных составляющих. В общем случае при подсчете громкости сложного звука следует учитывать взаимное влияние составляющих при их слуховом восприятии (эффект маскировки). При достаточно больших частотных интервалах между составляющими эффектом их взаимной маскировки можно с известным приближением пренебречь.
По найденной суммарной громкости с помощью номограммы (рисунок 6. 3 приложения) определяется уровень громкости звука гудка и звука воздуходувки. Вычисления сводим в таблицу.
|
|
|
| Звук гудка | Звук воздуходувки | ||||||
| Задано | Находится | Задано | Находится | ||||
| Частота fi, Гц | Уровень силы звука β i, дБ | по кривым равной громкости | по номограмме | Частота fi, Гц | Уровень силы звука β i, дБ | по кривым равной громкости | по номограмме |
| уровень громкости звука Li, фоны | громкость Gi, соны | уровень громкости звука Li, фоны | громкость Gi, соны | ||||
|
|
| ||||||
| по номограмме, Lэ | 116 фонов | по номограмме, Lэ, фон | 107 фонов | ||||
Уровень громкости гудка на 9 фонов больше, чем уровень громкости звука воздуходувки, т. е. звук гудка примерно вдвое громче звука воздуходувки.
|
|
|
