 |
Примеры решения задач. Задача 1. Скорость звука в прокладке с небольшими поперечными размерами по сравнению с длиной волны можно считать равной скорости звука в тонких стержнях
|
|
|
|
Примеры решения задач
Задача 1.
Поперечные размеры звукоизолирующей резиновой прокладки составляют несколько длин продольных волн. Оценить отношение скоростей продольных волн в подобной протяженной прокладке и в прокладках с небольшой опорной площадью, полагая коэффициент Пуассона данной резины μ = 0, 49
Решение:
Скорость звука в прокладке с небольшими поперечными размерами по сравнению с длиной волны можно считать равной скорости звука в тонких стержнях, так как боковые поверхности прокладки имеют возможность при колебаниях расширяться в стороны. В широкой резиновой прокладке скорость распространения продольных волн близка к скорости их распространения в безграничной среде. Используя формулы (2. 4) и (2. 5), получим искомое отношение скоростей звука в широкой и узкой прокладках в следующем виде:
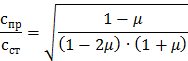
Для указанного значения μ = 0, 49 это отношение:
Ответ: 
Задача 2:
Колеблющаяся металлическая пластина граничит одной стороной с воздухом, а другой – с водой. Оценить соотношение величин звукового давления в воде и в воздухе.
Решение
Колебательные скорости частиц сред по обе стороны пластины равны. Из формулы (2. 14) видно, что в этом случае отношение звуковых давлений в обеих средах равно отношению акустических сопротивлений сред, т. е.:
Ответ: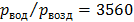 
Задача 3:
Определить скорость распространения изгибных волн с частотами 10 и 1000 Гц в стальной пластине толщиной 1 см. Каково отношение этой скорости к скорости распространения продольных волн?
Решение
По формуле (2. 7а) находим скорость распространения в пластине волн изгиба:
На частоте 10 Гц:
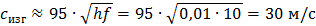
На частоте 1000 Гц:
Скорость распространения волн изгиба на частоте 1000 Гц в 10 раз больше скорости распространения той же волны на частоте 10 Гц. Скорость продольных волн в стержнях и пластинах из конструкционных металлов имеет величину порядка 5 км/с. Следовательно, скорость распространения продольных волн больше скорости распространения волн изгиба в металлической пластине толщиной 1 см на частоте 10 Гц примерно в 170 раз, на частоте 1000 Гц – в 17 раз.
|
|
|
Ответ: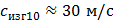 
; 
; скорость распространения продольных волн больше в 170, в 17 раз соответственно.
Задача 4
Звуковое давление на расстоянии 1 м от говорящего человека 0, 1 Па. Определить акустическую мощность эквивалентного источника, излучающего сферическую волну (полагая в первом приближении, что звук голоса следует этому закону).
Решение:
На основании формулы (2. 24):
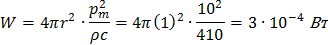
Как видно, акустическая мощность звуков речи невелика. Однако, акустическая мощность шумных механизмов может превышать десятки и сотни ватт.
Ответ: 
Задача 5
При работе ненаправленного точечного источника (т. е. источника весьма малых размеров), излучающего сферическую шумовую волну мощностью W, звуковое давление на фиксированном расстоянии равно p. Чему будет равно звуковое давление на этом расстоянии при увеличении числа источников некогерентного шумового излучения в n раз?
Решение:
Из формул (2. 26) и (2. 24) видно, что для шума величина звукового давления пропорциональна квадратному корню из мощности источника. Получаем для величины звукового давления при действии n источников:
В частности, при переходе от одного источника к двум давление возрастет примерно на 40%, при переходе к трем источникам – на 70% и т. п.
|
|
|
