Раздел 5. виброизоляция. 5.1. Виброизолирующий эффект упругих прокладок

Раздел 5. виброизоляция

Виброизоляция - это способность препятствовать распространению упругих волн и изолировать защищаемые корпусные конструкции от колебательной энергии источников вибрации.

Виброизоляция - установка на пути распространения колебаний волнового сопротивления, существенно отличного от волнового сопротивления материала вибропровода.

Под препятствием понимается как введение дополнительных конструктивных элементов, так и изменение инерционно-жесткостных параметров изолируемой части конструкции.

Виброизолирующий эффект - величина ослабления энергии колебаний конструкции после установки виброизолирующего препятствия

,

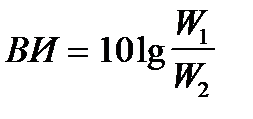где W₁ и W₂ - энергии колебаний конструкции за препятствием до и после установки препятствия.

В качестве препятствий используются упругие прокладки и виброзадерживающие массы.

 

5. 1. Виброизолирующий эффект упругих прокладок

Рассмотрим изоляцию колебаний упругой прокладкой распространяющихся продольно в бесконечном вибропроводе из материалов с большим акустическим сопротивлением. В качестве упругих прокладок обычно применяют резиновые элементы, т. к. в вибропроводе из материала с большим акустическим сопротивлением изолирующим элементом служит упругость, т. е. элемент, обладающий в диапазоне звуковых частот относительно малым акустическим сопротивлением.

Для однородной прокладки в бесконечном вибропроводе (например, валопровод с упругой звукоизолирующей муфтой, см. рис. 5. 1) будем иметь до упругой прокладки колебательную силу F₁ и скорость 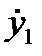 а после упругой прокладки соответственно F₂ и .

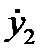F1

F2

r2c2

r1c1

r1c1

l

 

 

Рис. 5. 1 Схема установки упругой прокладки в бесконечном вибропроводе

Используя теорию четырехполюсников, обозначим упругий элемент симметричным четырехполюсником с коэффициентами А, В, С, D. Тогда уравнение четырехполюсника в матричной форме будет иметь вид

                                                              (5. 1)

откуда следует

  

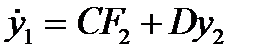                                                                                    (5. 2)

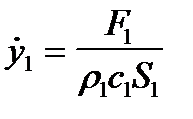,                                                     (5. 3)

Используя (5. 3), заменим в (5. 2) колебательные скорости через силы,

  и   ,

умножая обе части второго уравнения на r₁с₁S₁ и, складывая их с первым уравнением, получим 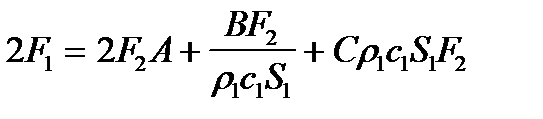. Разделив в полученном уравнении левую и правую части на 2F₂, запишем

                                         (5. 4)

       Подставляя в (5. 4) значения коэффициентов

получим    (5. 5)

Принимая во внимание, что в (5. 5) S₁=S₂, а r₂с₂< < r₁с₁, вторым слагаемым, как значительно более малым по сравнению с третьим, запишем

                                (5. 6)

Для низких частот аргумент 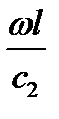 мал, тогда с достаточной для инженерных расчетов точностью можно считать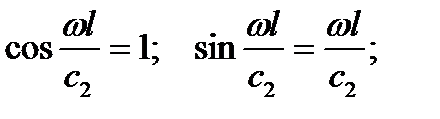

 Тогда (5. 6) будет иметь вид          (5. 7)

где  - жесткость прокладки на единицу площади;  - упругое сопротивление прокладки.

Анализируя (5. 7), можно видеть, что при  т. е. прокладка полностью пропускает колебательную энергию (колебательная сила не уменьшается). Это происходит при , где n=1, 2, 3...., l - длина волны в прокладке. Таким образом, если по длине прокладки укладывается целое число полуволн, то имеет место волновой резонанс, при котором упругая прокладка не является изолятором. Частоты таких резонансов

                                                                                            (5. 8)

Эффект виброизоляции будет максимальным при

Величина эффекта виброизоляции

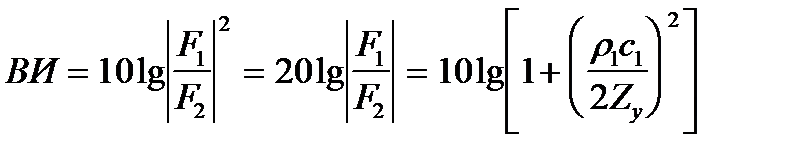     (5. 9)

т. к.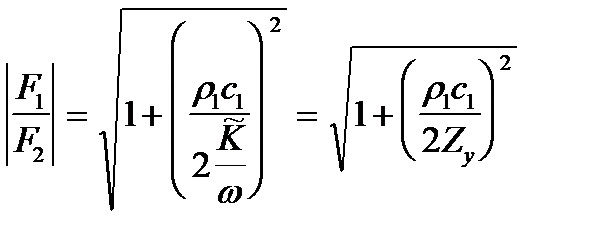

Выражение для определения эффекта виброизоляции изгибных волн упругой прокладкой имеет вид

 

                                           (5. 10)

где f_nn - частота полного пропускания изгибных волн

,                                        (5. 11)

где Е₁, Е₂ -модули упругости материалов вибропровода и прокладки; H - поперечный размер; 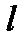 - толщина прокладки; с₂  - скорость звука в материале прокладки.

При частотах f > (3 - 3, 5) f_nn уравнение(5. 10) упрощается

AM; BM, CM r1 c1 S1

M

A, B, C r2 c2 S2

l

lM

                                                                  (5. 12)

AM, BM, CM

M

A =1; B=C=0

Для амортизированного механизма (рис. 5. 2) решение будет отличаться.

 

Рис. 5. 2. Схемы установки механизма на упругой прокладке (а) и при

жестком креплении механизма к абсолютно жесткому фундаменту (б).

 

В частности, матричное уравнение будет:

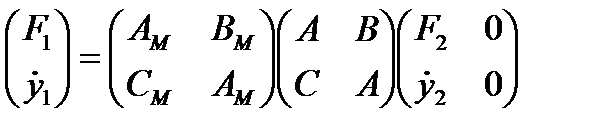                             (5. 13)

Т. к. Z_ф® ¥ , то в (5. 13) 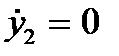, тогда, как и прежде, принимая во внимание, что r₂с₂S₂< < r₁c₁S₁ получим (полагая, что при жестком креплении механизма к фундаменту имеется прокладка длиной l=0); F₁=(A_MA+B_MC)F₂ и (F₁=F_2ЖА_М).

С учетом этого, можно записать

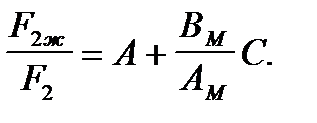                                                                        (5. 14)

Подставляя в (5. 14) вместо коэффициентов четырехполюсников их значения, получим

                                      (5. 15)

Для низких частот  - мало и уравнение (5. 15) будет

                                                 (5. 16)

где  - масса механизма.

Для малых величин , что имеет место на низких частотах и при малых толщинах прокладок, из (5. 15) следует

откуда  и эффективность виброизоляции

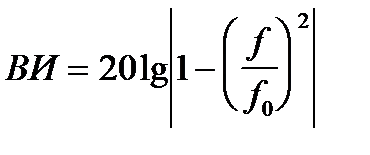                                                                     (5. 17)

Для диапазона частот удовлетворяющего условию f/f_o > 3 формула (5. 17) упрощается

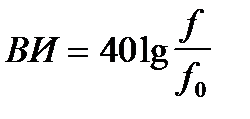                                                         (5. 18)

График зависимости виброизоляции механизма, установленного на упругих прокладках, (рис. 5. 3) связан с амплитудно - частотной характеристикой этой колебательной системы (см. рис. 5. 4).

 

Рис. 5. 3. Частотная зависимость виброизоляции однокаскадной амортизации

Рис. 5. 4. Амплитудно-частотная (а) и виброизолирующая (б) характеристики

 

⇐ Предыдущая12131415161718192021Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: