 |
Приведение общей ЗЛП к каноническому виду.
|
|
|
|
ВВЕДЕНИЕ
Современная экономическая теория, как на микро –, так и на макро–уровне, включает как естественный, необходимый элемент математические модели и методы. Использование математики в экономике позволяет, во–первых, выделить и формально описать наиболее важные, существенные связи экономических переменных и объектов: изучение столь сложного объекта предполагает высокую степень абстракции. Во–вторых, из четко сформулированных исходных данных и соотношений методами дедукции можно получать выводы, адекватные изучаемому объекту в той же мере, что и сделанные предпосылки. В–третьих, методы математики и статистики позволяют индуктивным путем получать новые знания об объекте: оценивать форму и параметры зависимостей его переменных, в наибольшей степени соответствующие имеющимся наблюдением. Наконец, в–четвертых, использование языка математики позволяет точно и компактно излагать положения экономической теории, формулировать ее понятия и выводы.
Математические модели, используемые в экономике, можно подразделять на классы по ряду признаков, относящихся к особенностям моделируемого объекта, цели моделирования и используемого инструментария: модели микро– и макроэкономические, теоретические и равновесные, статистические и динамические.
Суть методов оптимизации заключается в том, что исходя из наличия определенных ресурсов выбирается такой способ их использования (распределения), при котором обеспечивается максимум (минимум) интересующего нас показателя.
В качестве методов оптимизации в экономике находят применение все основные разделы математического программирования (планирования).
Математическая дисциплина, занимающаяся изучением экстремальных (максимальных или минимальных) задач управления, планирования и разработкой методов их решения, получила название математического программирования.
|
|
|
В общем, виде математическая постановка экстремальной задачи состоит в определении наибольшего или наименьшего значения целевой функции 
при условии 
,
где 
и 
– заданные функции, а 
– некоторые действительные числа.
В зависимости от вида функции цели и ограничений математическое программирование делится на линейное и нелинейное. Наиболее
изученным разделом математического программирования является линейное программирование.
Определение. Линейное программирование – наука о методах использования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения.
Эта линейная функция называется целевой, а ограничения в виде уравнений или неравенств, называется системой ограничений.
Определение. Математическое выражение целевой функции и ее ограничений называется математической моделью экономической задачи.
Рассмотрим некоторые задачи линейного программирования (ЗЛП).
1. Задача об использовании ресурсов (задача планирования производства).
Для изготовления различных изделий 
предприятие использует три различных вида сырья. Нормы расхода сырья на производство одного изделия 
, а также общее количество
сырья каждого вида, которое может быть использовано предприятием, приведены в табл.
| Вид сырья | Нормы затрат сырья(кг) на одно изделие | Общее кол–во сырья (кг) | ||
| 
| 
| ||
| I | ||||
| II | ||||
| III | ||||
| Цена одного изделия (грн.) |
Составить план производства изделий, при котором общая стоимость всей произведенной предприятием продукции является максимальной.
Построим математическую модель данной задачи.
|
|
|
Обозначим через 
искомый выпуск изделий 
, через 
– изделий 
,
через 
– изделий 
. Так как на сырье каждого вида имеются нормы затрат, тогда мы можем найти общий объем затрат сырья каждого вида для изготовления всех изделий. Из таблицы следует, что общий объем сырья I вида составит 
, II – 
,
III – 
. А так как на фонд сырья имеются ограничения, следовательно общий объем сырья каждого вида должен быть не больше общего количества сырья, т.е. получим следующую систему неравенств
(1)
По экономическому смыслу переменные 
могут принимать только неотрицательные значения:
(2)
Стоимость всех изделий вида составит 
– 
– 
Соответственно общая стоимость произведенной предприятием продукции составит 
(3)
Нам необходимо найти 
этой функции. Таким образом, необходимо среди всех неотрицательных решений системы (1) требуется найти такое, при котором функция (3) принимает максимальное значение.
Данную задачу можно легко обобщить на случай выпуска 
видов изделий с использованием 
видов сырья (ресурсов).
Обозначим через 
– число единиц продукции запланированной к производству, 
– запас ресурсов 
– го вида, 
– удельный расход 
– го ресурса для изготовления 
– ой продукции. 
– прибыль от реализации единицы изделия – го вида.
Тогда экономико – математическая модель задачи об использовании ресурсов в общей постановке примет вид: найти такой план 
выпуска продукции, удовлетворяющий основной системе ограничений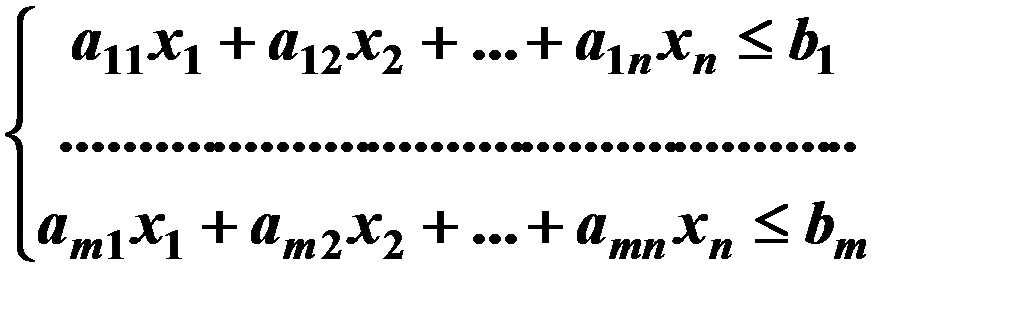 
дополнительной системе ограничений
при котором целевая функция 
– 
принимает максимальное значение.
Замечание. Чтобы составить математическую модель ЗЛП необходимо:
– ввести обозначения переменных;
– исходя из цели экономических исследований, составить целевую функцию;
– учитывая ограничения в использовании экономических показателей задачи и их количественные закономерности, записать систему ограничений.
Решение задач линейного программирования основываются на понятиях аналитической геометрии в – мерном векторном пространстве.
Приведение общей ЗЛП к каноническому виду.
Общий вид ЗЛП следующий:
(1)
(2)
(3)
где соотношение (1) – целевая функция, (2) – система основных ограничений, (3) – система дополнительных ограничений.
|
|
|
Соотношения (2) и (3) образуют полную систему ограничений.
Приведение системы основных ограничений к каноническому виду осуществляется введением в левые части неравенств дополнительных неотрицательных переменных с коэффициентами «+1», если неравенства вида 
и «-1», если неравенства вида 
. В целевую функцию дополнительные переменные входят с нулевыми коэффициентами.
Определение. ЗЛП называется заданной в каноническом виде, если ее система основных ограничений представлена уравнениями.
Определение. ЗЛП называется заданной в стандартной форме канонического вида, если выполняются следующие условия:
1) система основных ограничений представлена уравнениями и все они линейно независимы;
2) число уравнений меньше числа переменных;
3) решается задача минимизации целевой функции;
4) правые части системы основных ограничений неотрицательны;
5) все переменные также неотрицательны.
|
|
|
