 |
Формы записи ЗЛП. Основные определения.
|
|
|
|
Существуют несколько форм записи ЗЛП.
1. Развернутая форма записи:

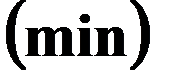



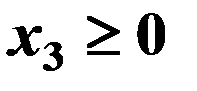
2. Форма записи с помощью знаков суммирования имеет вид:


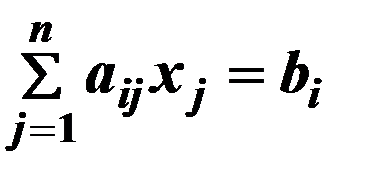



3. Матричная форма записи ЗЛП:
Обозначим через  – матрицу системы основных ограничений;
– матрицу системы основных ограничений;
 – матрицу–столбец неизвестных;
– матрицу–столбец неизвестных;
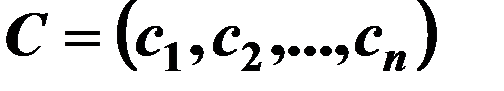 – матрицу–строку коэффициентов при неизвестных в целевой функции;
– матрицу–строку коэффициентов при неизвестных в целевой функции;
 – матрицу–столбец свободных чисел.
– матрицу–столбец свободных чисел.
Тогда ЗЛП можно записать в следующим образом:

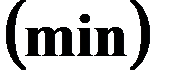


4. Векторная форма записи ЗЛП:
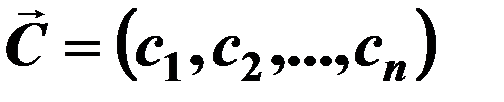 ;
;  ;
;  ;
;
 ;…….;
;…….; 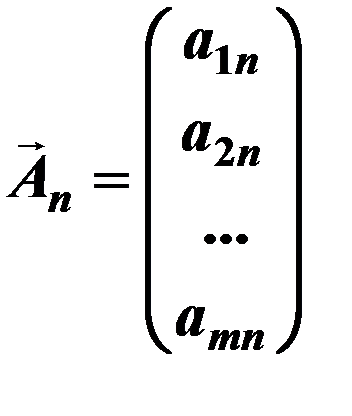 ;
; 
Тогда

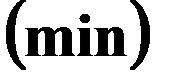


Определение. Планом ЗЛП называется набор значений переменных  , удовлетворяющий полной системе ограничений.
, удовлетворяющий полной системе ограничений.
Определение. Решением ЗЛП или оптимальным планом, называется план, доставляющий целевой функции заданный вид экстремума.
Определение. План ЗЛП называется опорным, если его положительным компонентам соответствует система линейно независимых векторов.
Определение. Опорный план ЗЛП называется невырожденным, если векторы, соответствующие его положительным компонентам, образуют базис.
В противном случае опорный план называется вырожденным.
Методы решения задач линейного программирования
Графоаналитический метод решения ЗЛП.
Графоаналитический метод решения есть наиболее простым и наглядным метолом линейного программирования. Этот метод применяется, в основном, для решения ЗЛП с двумя переменными и только иногда для решения задач трехмерного пространства.
Можно выделить два способа графоаналитического решения ЗЛП: способ полного перебора и способ направленного перебора, или градиентный способ.
Алгоритм решения задач.
Способ полного перебора.
1. Находим область допустимых решений системы ограничений задачи, т.е. строим множество  и оцениваем его:
и оцениваем его:
|
|
|
а) если  (пустое мн–во), то решений нет;
(пустое мн–во), то решений нет;
б) если  – выпуклая многогранная область, то метод не применим;
– выпуклая многогранная область, то метод не применим;
в) если  – выпуклый многоугольник, то переходим к следующему этапу решения.
– выпуклый многоугольник, то переходим к следующему этапу решения.
2. Определяем координаты угловых точек множества  .
.
3. Вычисляем значение целевой функции в каждой точке множества  и определяем точки экстремума:
и определяем точки экстремума:
– если требуемый экстремум достигается в одной точке, то ЗЛП имеет единственное решение и координаты этой точки являются оптимальным планом;
– если требуемый экстремум достигается в двух угловых точках, то ЗЛП имеет бесчисленное множество решений, которыми являются координаты любой точки отрезка, соединяющие данные угловые точки.
Способ направленного перебора.
1. Строим множество  и оцениваем его:
и оцениваем его:
а) если  , то решений нет;
, то решений нет;
б) если  – выпуклый многоугольник или выпуклая многогранная область, то переходим ко второму этапу решения.
– выпуклый многоугольник или выпуклая многогранная область, то переходим ко второму этапу решения.
2. Строим вектор–градиент  ,
, 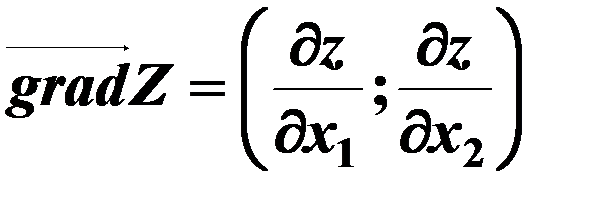 .
.
3. Проводим линию уровня  , которая перпендикулярна вектору
, которая перпендикулярна вектору  .
.
4. Линию уровня перемещаем по направлению вектора  , ели задача на максимум и в направлении противоположном
, ели задача на максимум и в направлении противоположном  , для задачи на минимум, до тех пор пока она не станет опорной для множества
, для задачи на минимум, до тех пор пока она не станет опорной для множества  .
.
Определение. Прямая называется опорной для многоугольника, если:
1. Она имеет общие точки с этим многоугольником;
2. Все точки этого многоугольника лежат по одну сторону от этой прямой.
3. Находим координаты точки экстремума и вычисляем значение целевой функции в ней.
Симплексный метод.
Среди универсальных методов решения ЗЛП наиболее распространен симплексный метод (или симплекс–метод), т.к. позволяет решить практически любую ЗЛП в канонической форме. Этот метод был разработан американским ученым Дж. Данцигом.
Идея симплекс–метода заключается в том, что начиная с некоторого исходного опорного плана решения путем последовательного улучшения исходного, за определенное число этапов (итераций), приходим к оптимальному. Симплекс–метод основан на следующих свойствах ЗЛП:
|
|
|
1. Если экстремум существует, то он единственный;
2. Множество всех планов ЗЛП выпукло;
3. Целевая функция ЗЛП достигает своего максимального (минимального) значения в угловой точке многогранника решений (в его вершине). Если целевая функция принимает свое оптимальное значение более, чем в одной точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.
4. Каждой угловой точке многогранника решений отвечает опорный план ЗЛП.
Алгоритм решения ЗЛП симплексным методом.
1. Математическая модель задачи должна быть канонической. Если она неканоническая, то ее надо привести к каноническому виду.
2. Находим исходное опорное решение (план) и проверяем его на оптимальность, для этого составляем симплекс–таблицу.
| Б | 
| 
| 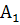
| 
| … | 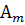
| 
| 
|

| 
| … | 
| 
| ||||
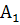
| 
| … | 
| |||||

| 
| … | 
| |||||
| … | … | … | … | … | … | … | … | |
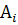
| 
| … | 
| |||||
| … | … | … | … | … | … | … | … | |
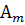
| 
| … | 
| |||||

| 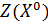
| … | 
|
В столбцах записываются:
Б – базисные вектора;
 – коэффициенты целевой функции при базисных переменных;
– коэффициенты целевой функции при базисных переменных;
 – коэффициенты целевой функции;
– коэффициенты целевой функции;
Строка 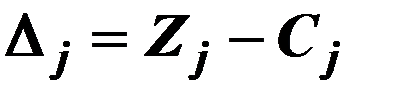 – называется индексной строкой, ее значения находятся по формуле:
– называется индексной строкой, ее значения находятся по формуле:

По оценкам векторов проверяем оптимальность плана. Возможны следующие случаи:
а) если все оценки  , то на основании признака оптимальности исходный опорный план является оптимальным.
, то на основании признака оптимальности исходный опорный план является оптимальным.
Критерий оптимальности. Опорный план задачи является оптимальным, если оценки  неотрицательны (для задачи на максимум);
неотрицательны (для задачи на максимум);
б) если хотя бы одна оценка  и все соответствующие этому индексу величины не положительны, то целевая функция не ограничена на множестве планов, решение задачи прекращаем, т.е. ЗЛП не имеет решений;
и все соответствующие этому индексу величины не положительны, то целевая функция не ограничена на множестве планов, решение задачи прекращаем, т.е. ЗЛП не имеет решений;
в) если хотя бы одна оценка отрицательна, а при соответствующей переменной есть хотя бы один положительный коэффициент, то нужно перейти к другому опорному решению;
г) если отрицательных оценок несколько, то в столбец базисной переменной вводят ту переменную, которой соответствует наибольшая по абсолютной величине отрицательная оценка.
|
|
|
Столбец которому соответствует наибольшая по абсолютной величине отрицательная оценка называется ключевым столбцом. За ключевую строку принимают ту, которой соответствует минимальное отношение свободных членов к положительным коэффициентам ключевого столбца.
Элемент, находящийся на пересечении ключевых строки и столбца, называется ключевым элементом.
3. Заполняем симплекс–таблицу 2–го шага:
а) переписываем ключевую строку, разделив ее на ключевой элемент;
б) заполняем базисные столбцы;
в) остальные коэффициенты пересчитываем по правилу «прямоугольника». Правило «прямоугольника» заключается в следующем:
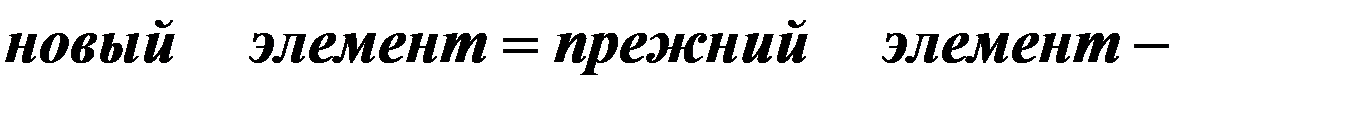

Оценки можно пересчитывать, как в первой таблице или правилу «прямоугольника».
4. Проверяем новый опорный план на оптимальность. Если план не оптимальный и необходимо перейти к новому, то возвращаемся к пункту 3. Если план оптимальный или установлено, что неразрешима, то процесс решения задачи заканчиваем.
Замечание. Если целевая функция требует нахождения минимального значения, то критерием оптимальности задачи является не положительность оценок.
|
|
|


