 |
Рассмотрим задачу об использовании ресурсов
|
|
|
|
 (max)
(max)

 ,
,  ,
,  .
.
Приведем задачу к каноническому виду. Введем при дополнительные переменные, получим:
 (max)
(max)

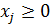 ,
, 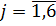
Эти дополнительные переменные по экономическому смыслу означают не используемое при данном плане производства количество сырья того или иного вида. Например, – это неиспользуемое количество сырья 1–го вида. Запишем систему основных ограничений в векторной форме:
 ,
,  ,
, 

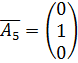 ,
, 

Вектора  ,
, 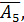
 – ЛНЗ, следовательно они образуют базис. Переменные
– ЛНЗ, следовательно они образуют базис. Переменные 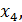
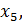
 – базисные переменные,
– базисные переменные,  – свободные переменные. Запишем первоначальный опорный план
– свободные переменные. Запишем первоначальный опорный план 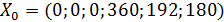 .
.
Для оценки плана составим первую симплексную таблицу.
| Б | 
| 
| 
| 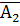
| 
| 
| 
| 
| 
| 
| 
|

| |||||||||||

| |||||||||||

| |||||||||||

| –9 | –10 | –16 | –180 | –240 | –384 |
Проведем экономический анализ первой симплекс–таблицы. Дополнительные переменные принимают значения, которые совпадают с лимитами ресурсов предприятия, т.е. они совсем не используются и значения целевой функции равно нулю, т.е. не создают прибыль. Производство не запущено, прибыль равна нулю. Полученный план оптимальным не является. Это видно из индексной строки, т.к. имеются три отрицательные оценки. Эти оценки свидетельствуют не только о возможности увеличения прибыли, но и на сколько ее можно увеличить при введении в план производства единицы того или иного вида продукции. Так, например, число 9 означает, что при введении в план производства одного изделия вида А прибыль увеличится на 9 грн. Если в план производства ввести по одной единице продукции В и С, то прибыль соответственно составит 10 и 16 грн. С экономической точки зрения следует, что наиболее выгодным является включение в план производства продукции вида С. Это же необходимо сделать исходя из алгоритма решения ЗЛП симплекс–методом. Т.к. число –16 является максимальным по абсолютной величине, то вектор  необходимо ввести в базис. Определим вектор, который необходимо вывести из базиса. Для этого находим
необходимо ввести в базис. Определим вектор, который необходимо вывести из базиса. Для этого находим  ;
;  ,
,  , т.е.
, т.е.  или
или 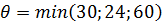 .
.
|
|
|
С экономической точки зрения мы определили какое количество изделий С предприятие может изготовить с учетом норм расходов и имеющихся объемов сырья каждого вида. Учитывая объем сырья и нормы расходов максимальное количество изделий вида С равно 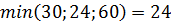 , т.е. ограничивающим фактором для производства изделий вида С, является объем сырья 2–го вида. Т.е. предприятие может произвести 24 единицы изделия вида С, при этом сырье 2–го вида будет израсходовано полностью. Следовательно, вектор
, т.е. ограничивающим фактором для производства изделий вида С, является объем сырья 2–го вида. Т.е. предприятие может произвести 24 единицы изделия вида С, при этом сырье 2–го вида будет израсходовано полностью. Следовательно, вектор  выводим из базиса. Столбец вектора
выводим из базиса. Столбец вектора  и строка вектора
и строка вектора 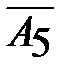 являются ключевыми, число 8, стоящее на пересечении является ключевым элементом. Составим вторую симплексную таблицу.
являются ключевыми, число 8, стоящее на пересечении является ключевым элементом. Составим вторую симплексную таблицу.

| 
| 
| 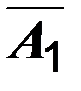
| 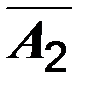
| 
| 
| 
| 
| 
|

| -12/8 | 72/9=8 | |||||||

| 6/8 | 4/8 | 1/8 | 24:4/8=48 | |||||

| 22/8 | 12/8 | -3/8 | 108:12/8=72 | |||||

| -2 |  8 (-2)=–16 8 (-2)=–16
|
Мы получили новый опорный план  . При данном плане производство выпускает 24 единицы изделий вида С и при этом остается не использованным 72 единицы сырья 1–го вида и 108 единиц сырья 3–го вида, а прибыль составит 384грн.
. При данном плане производство выпускает 24 единицы изделий вида С и при этом остается не использованным 72 единицы сырья 1–го вида и 108 единиц сырья 3–го вида, а прибыль составит 384грн.
Рассмотрим экономическое содержание, например, столбца  . Число
. Число  во второй строке означает на сколько необходимо уменьшить выпуск изделия С, если запланировать выпуск одного изделия В. Число 9 и
во второй строке означает на сколько необходимо уменьшить выпуск изделия С, если запланировать выпуск одного изделия В. Число 9 и  показывают, соответственно, сколько потребуется сырья 1 и 3 вида при включении в план производства одного изделия вида В, а число –2 в индексной строке показывает на сколько увеличится прибыль предприятия. Другими словами, если в план производства включить одно изделие вида В, то при этом потребуется уменьшить выпуск изделия вида С на
показывают, соответственно, сколько потребуется сырья 1 и 3 вида при включении в план производства одного изделия вида В, а число –2 в индексной строке показывает на сколько увеличится прибыль предприятия. Другими словами, если в план производства включить одно изделие вида В, то при этом потребуется уменьшить выпуск изделия вида С на  и дополнительных затрат 9 ед. сырья 1–го вида и
и дополнительных затрат 9 ед. сырья 1–го вида и  ед. сырья 3–го вида, а общая прибыль возрастет на 2грн. Аналогичный экономический смысл имеют элементы столбца
ед. сырья 3–го вида, а общая прибыль возрастет на 2грн. Аналогичный экономический смысл имеют элементы столбца  , а вот элементы столбца
, а вот элементы столбца  имеют несколько иное экономическое содержание. Так число
имеют несколько иное экономическое содержание. Так число 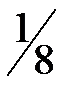 показывает, что при увеличении объемов сырья 2–го вида на одну единицу выпуск изделия вида С увеличится на
показывает, что при увеличении объемов сырья 2–го вида на одну единицу выпуск изделия вида С увеличится на  ед. Для этого потребовалось бы увеличить объем сырья 1–го вида на
ед. Для этого потребовалось бы увеличить объем сырья 1–го вида на  ед., а 3–го вида –на
ед., а 3–го вида –на  ед. При этом прибыль предприятия увеличилась бы на 2грн.
ед. При этом прибыль предприятия увеличилась бы на 2грн.
|
|
|
План полученный во второй итерации оптимальным не является, т.к. есть отрицательная оценка. Следовательно, в план необходимо ввести вектор 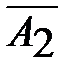 , т.е. в новом плане следует предусмотреть выпуск изделия вида В. Для определения вектора выводимого из базиса, пользуемся аналогичными рассуждениями приведенными выше. Из базиса будем выводить вектор
, т.е. в новом плане следует предусмотреть выпуск изделия вида В. Для определения вектора выводимого из базиса, пользуемся аналогичными рассуждениями приведенными выше. Из базиса будем выводить вектор 
Следующую симплекс–таблицу составляем аналогично 2–ой итерации.

| 
| 
| 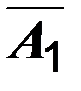
| 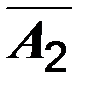
| 
| 
| 
| 
| |

| 1/9 | -1/6 | |||||||

| 1/4 | -1/18 | 5/24 | ||||||

| 5/4 | -1/6 | -1/8 | ||||||

| 2/9 | 5/3 |
Получили новый опорный план 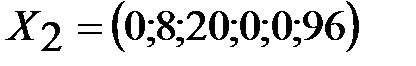 и проверяем его на оптимальность. Т.к. в индексной строке все оценки являются не отрицательными, то найденный опорный план оптимальный и
и проверяем его на оптимальность. Т.к. в индексной строке все оценки являются не отрицательными, то найденный опорный план оптимальный и 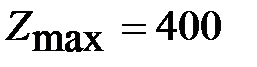 . Оптимальный план выпуска изделий состоит из 8 единиц продукции вида В и 20 – вида С, при этом плане полностью израсходовано сырье 1 и 2 вида, а сырье 3 вида осталось в количестве 96 ед., а прибыль составляет 400грн.
. Оптимальный план выпуска изделий состоит из 8 единиц продукции вида В и 20 – вида С, при этом плане полностью израсходовано сырье 1 и 2 вида, а сырье 3 вида осталось в количестве 96 ед., а прибыль составляет 400грн.
Двойственность в ЛП.
Каждой задаче ЛП можно определенным образом сопоставить некоторую другую ЗЛП, называемой двойственной. Первоначальная задача является исходной. Эти две задачи тесно связаны между собой и образуют единую двойственную пару.
Различают симметричную, несимметричную и смешанные задачи. Мы рассмотрим только симметричную задачу, т.к. рассматриваемая нами задача об использовании ресурсов и двойственная к ней образуют симметричную пару. Запишем эти задачи. Дана исходная задача



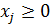 ,
, 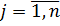 ,
, 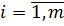
Составим математическую модель двойственной задачи, для этого:
|
|
|
– каждому неравенству системы ограничений исходной задачи (ИЗ) приводим в соответствие переменную;
–составляем целевую функцию, коэффициентами которой являются свободные члены системы ограничений ИЗ;
– составляем систему ограничений. Коэффициенты системы ограничений образуют транспонированную матрицу системы ограничений ИЗ. Знаки неравенств меняются на противоположные;
– свободными членами системы ограничений являются коэффициенты целевой функции ИЗ. Все переменные двойственной задачи не отрицательны.
Математическая модель двойственной задачи имеет вид:
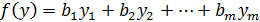


 ,
,  ,
, 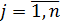
Основные теоремы двойственности.
Первая теорема двойственности. Если одна из двойственных задач имеет оптимальное решение, то другая также имеет оптимальное решение, при этом значения целевых функций на оптимальных решениях совпадают
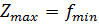 .
.
Если целевая функция одной из двойственных задач неограниченна на множестве планов, то другая задача при этом не имеет решений.
Вторая теорема двойственности. Пусть  –допустимое решение ИЗ, а
–допустимое решение ИЗ, а  – допустимое решение ДЗ. Для того, чтобы решения были оптимальными необходимо и достаточно, чтобы выполнялись следующие условия:
– допустимое решение ДЗ. Для того, чтобы решения были оптимальными необходимо и достаточно, чтобы выполнялись следующие условия:
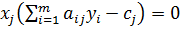 ,
, 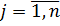
 ,
, 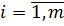
Теоремы позволяют определить оптимальное решение одной из пары задач по решению другой.
Построим двойственную задачу, найдем ее решение и дадим экономическую оценку с помощью двойственных оценок на примере, рассматриваемой нами задачи об использовании ресурсов. Запишем ИЗ
 (max)
(max)

 ,
,  ,
,  .
.
Сформулируем двойственную задачу (ДЗ). Предположим, что некоторая организация решила закупить все ресурсы рассматриваемого предприятия. Для этого необходимо установить оптимальную цену на приобретаемые ресурсы  ,
, 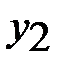 ,
,  , причем:
, причем:
1) покупающая организация старается минимизировать общую стоимость ресурсов;
2) за каждый вид ресурсов необходимо заплатить не менее той суммы, которую предприятие может выручить при переработке сырья в готовую продукцию.
Тогда, согласно первому условию общая стоимость сырья будет:
|
|
|
 .
.
Согласно второму требованию вводятся ограничения: на единицу А вида продукции расходуется 18 единиц первого ресурса ценой  , 6 ед. второго ресурса ценой
, 6 ед. второго ресурса ценой 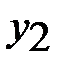 , 5 ед. третьего ресурса ценой
, 5 ед. третьего ресурса ценой  . Стоимость всех ресурсов, расходуемых на производство единицы продукции вида А, равна
. Стоимость всех ресурсов, расходуемых на производство единицы продукции вида А, равна
 и должна составить не менее 9, т.е.
и должна составить не менее 9, т.е.  .
.
Аналогичные рассуждения проводим для продукции вида В и С и получаем систему неравенств:

 ,
, 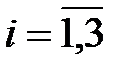
Получили математическую модель двойственной задачи. В результате решения ИЗ было получено следующее решение:

| 
| 
| 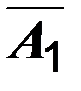
| 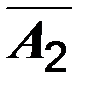
| 
| 
| 
| 
|

| 1/9 | -1/6 | ||||||

| 1/4 | -1/18 | 5/24 | |||||

| 5/4 | -1/6 | -1/8 | |||||

| 2/9 | 5/3 |
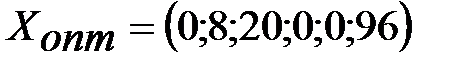 ;
;  . Для получения решения ДЗ можно воспользоваться решением ИЗ. По первой теореме двойственности
. Для получения решения ДЗ можно воспользоваться решением ИЗ. По первой теореме двойственности
 . Значение компонент оптимального плана ДЗ не требует дополнительных вычислений – они расположены в индексной строке последней симплексной таблицы ИЗ на пересечении со столбцами векторов, входящих в начальный базис, если к содержимому прибавить коэффициенты целевой функции при соответствующей переменной. Следовательно,
. Значение компонент оптимального плана ДЗ не требует дополнительных вычислений – они расположены в индексной строке последней симплексной таблицы ИЗ на пересечении со столбцами векторов, входящих в начальный базис, если к содержимому прибавить коэффициенты целевой функции при соответствующей переменной. Следовательно,  ;
;  ;
;  .
.  . Т.к.
. Т.к. 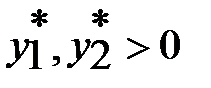 , то 1 и 2 вид сырья являются дефицитными, в оптимальном плане ИЗ они полностью использованы.
, то 1 и 2 вид сырья являются дефицитными, в оптимальном плане ИЗ они полностью использованы.  следовательно 3 вид сырья недефицитный, в оптимальном плане ИЗ он использован не полностью. Можно сделать вывод, что если условные двойственные оценки больше 0, то ресурс является дефицитным, а если равны 0, то недефицитный. Таким образом, положительную двойственную оценку имеют те виды сырья, которые полностью использованы при оптимальном плане производства продукции. Величина двойственной оценки показывает, на сколько возрастает максимальное значение целевой функции ИЗ при увеличении количества сырья соответствующего вида на 1 ед. Так, увеличение количества сырья 1–го вида на 1 ед. приводит к тому, что можно найти новый оптимальный план производства, при котором общая стоимость увеличится на 2/9 и будет равна
следовательно 3 вид сырья недефицитный, в оптимальном плане ИЗ он использован не полностью. Можно сделать вывод, что если условные двойственные оценки больше 0, то ресурс является дефицитным, а если равны 0, то недефицитный. Таким образом, положительную двойственную оценку имеют те виды сырья, которые полностью использованы при оптимальном плане производства продукции. Величина двойственной оценки показывает, на сколько возрастает максимальное значение целевой функции ИЗ при увеличении количества сырья соответствующего вида на 1 ед. Так, увеличение количества сырья 1–го вида на 1 ед. приводит к тому, что можно найти новый оптимальный план производства, при котором общая стоимость увеличится на 2/9 и будет равна  . А числа, стоящие в столбце показывают, что полученное увеличение прибыли может быть достигнуто за счет увеличения выпуска изделия В на 1/9 ед. и сокращении выпуска изделия С на 1/18 ед., а расход сырья 3–го вида возрастет на 1/6 ед. Аналогичный анализ мы можем сделать и для 2–го вида сырья. При подстановке оптимальных двойственных оценок в систему ограничений двойственной задачи, получим:
. А числа, стоящие в столбце показывают, что полученное увеличение прибыли может быть достигнуто за счет увеличения выпуска изделия В на 1/9 ед. и сокращении выпуска изделия С на 1/18 ед., а расход сырья 3–го вида возрастет на 1/6 ед. Аналогичный анализ мы можем сделать и для 2–го вида сырья. При подстановке оптимальных двойственных оценок в систему ограничений двойственной задачи, получим:

Первое ограничение двойственной задачи выполняется как строгое неравенство. Это означает, что двойственная оценка сырья, используемого на производство изделия вида А выше цены этого изделия, следовательно, выпускать изделие вида А невыгодно. Его производство и не предусмотрено оптимальным планом ИЗ. Второе и третье ограничения двойственной задачи выполняются как равенства. Это означает, что двойственные оценки сырья, используемые для изготовления единицы изделия В и С соответственно, равны их ценам. Следовательно, выпуск этих изделий по двойственным оценкам экономически целесообразен. Их производство и предусмотрено оптимальным планом ИЗ. Таким образом, двойственные оценки тесно связаны с оптимальным планом прямой задачи.
|
|
|
Транспортная задача.
Цель транспортной задачи состоит в разработке наиболее рациональных путей и способов транспортирования товаров, устранение чрезмерно дальних, встречных, повторных перевозок. Все это сокращает время продвижения товаров, уменьшает затраты предприятий, фирм, связанные с осуществлением процессов снабжения сырьем, материалами, топливом, оборудованием и т.д.
Общая постановка транспортной задачи состоит в следующем: в  пунктах производства
пунктах производства 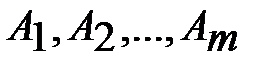 имеется однородный груз в количестве соответственно
имеется однородный груз в количестве соответственно  . Этот груз необходимо доставить в
. Этот груз необходимо доставить в  пунктов назначения
пунктов назначения  в количестве соответственно
в количестве соответственно  . Стоимость перевозки единицы груза (тариф) из пункта
. Стоимость перевозки единицы груза (тариф) из пункта  в пункт
в пункт  равна
равна  . Требуется составить план перевозок, позволяющий вывести все грузы и имеющий минимальную стоимость.
. Требуется составить план перевозок, позволяющий вывести все грузы и имеющий минимальную стоимость.
Общее наличие груза у поставщиков рано 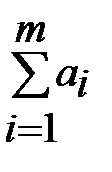 , общая потребность в грузе в пунктах назначения равна
, общая потребность в грузе в пунктах назначения равна 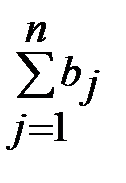 , тогда, если
, тогда, если  , то задача называется закрытой. Если
, то задача называется закрытой. Если  , то открытой. Обозначим через
, то открытой. Обозначим через 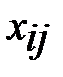 количество груза перевозимого из
количество груза перевозимого из  в пункт
в пункт  . Запишем условие задачи в виде таблицы.
. Запишем условие задачи в виде таблицы.


| 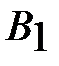
| 
| … | 
| … | 
| |
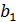
| 
| … | 
| 
| |||
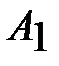
| 
| 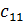

| 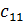

| … | 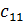

| … | 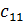

|

| 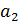
| 

| 

| … | 

| … | 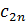
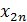
|
| … | … | … | … | … | … | … | … |
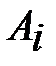
| 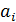
| 

| 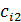

| 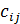

| 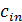

| ||
| … | … | … | … | … | … | … | … |

| 
| 

| 

| … | 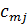

| .. | 

|
Транспортная задача как ЗЛП может быть решена симплексным методом, но для решения транспортной задачи разработан специальный метод, имеющий те же этапы, что и симплексный, а именно:
– нахождение исходного опорного решения;
– проверка этого решения на оптимальность;
– переход от одного опорного плана к другому.
Нахождение исходного опорного плана.
Условие задачи и ее исходное опорное решение будем записывать в распределительную табл. Существует несколько способов нахождения исходного опорного решения. Рассмотрим один из них – метод минимального тарифа (элемента). Согласно этому методу, грузы распределяются в первую очередь в те клетки, к которых находится минимальный тариф перевозок 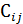 . Далее поставки распределяются в незанятые клетки с наименьшими тарифами с учетом оставшихся запасов у поставщиков и удовлетворения спроса потребителей. Процесс распределения продолжается до тех пор, пока все грузы от поставщиков не будут вывезены, а потребители не будут удовлетворены. При распределении грузов может оказаться, что кол-во занятых клеток меньше, чем
. Далее поставки распределяются в незанятые клетки с наименьшими тарифами с учетом оставшихся запасов у поставщиков и удовлетворения спроса потребителей. Процесс распределения продолжается до тех пор, пока все грузы от поставщиков не будут вывезены, а потребители не будут удовлетворены. При распределении грузов может оказаться, что кол-во занятых клеток меньше, чем  . В этом случае недостающее их число заполняется клетками с нулевыми поставками.
. В этом случае недостающее их число заполняется клетками с нулевыми поставками.
Пример.



Решение.
Проверяем, является ли данная задача закрытой или открытой. Для этого находим
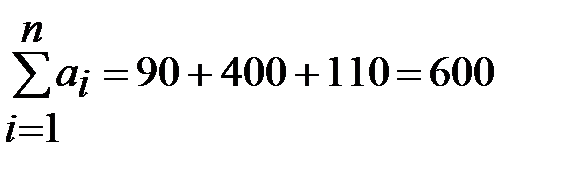 ,
,  , т.к.
, т.к. 
 , то данная задача закрытая. Найдем исходное решение методом минимального тарифа.
, то данная задача закрытая. Найдем исходное решение методом минимального тарифа.


| 
| 
| 
| |

| 2 | 2 | ||

| ||||

| 3 | 8 |
Т.к. число заполненных клеток равно 5 и m+n-1= 3+3-1=5, то план невырожденный. Полученное исходное опорное решение имеет вид:
 . Стоимость перевозки при данном опорном плане составит:
. Стоимость перевозки при данном опорном плане составит:  усл.ден.ед.
усл.ден.ед.
Проверка опорного плана на оптимальность.
Найденное исходное опорное решение проверяем на оптимальность. Для проверки оптимальности плана воспользуемся методом потенциалов. Для этого в таблице добавим строку  и столбец
и столбец 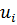 . Потенциалы будем находить и равенства
. Потенциалы будем находить и равенства  для заполненных клеток. Числа
для заполненных клеток. Числа 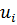 и
и  называются потенциалами. Одному из потенциалов припишем произвольное значение, например
называются потенциалами. Одному из потенциалов припишем произвольное значение, например  , тогда остальные потенциалы определяются однозначно. Если известен потенциал
, тогда остальные потенциалы определяются однозначно. Если известен потенциал 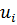 то
то  , если известен потенциал
, если известен потенциал  то
то  . После того, как все потенциалы найдены, найдем
. После того, как все потенциалы найдены, найдем  . Эту оценку называют оценочной. Если для всех незаполненных клеток
. Эту оценку называют оценочной. Если для всех незаполненных клеток  , то полученный план является оптимальным, если хотя бы одна оценка
, то полученный план является оптимальным, если хотя бы одна оценка  , то опорный план оптимальным не является и его можно улучшить. Если хотя бы одна оценка равна нулю то ТЗ имеет бесчисленное множество решений.
, то опорный план оптимальным не является и его можно улучшить. Если хотя бы одна оценка равна нулю то ТЗ имеет бесчисленное множество решений.
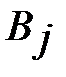
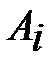
| 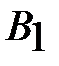
| 
| 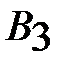
|

| |
| 2 – | 2 + | |||
| |||||

| 3 + | 8 – | |||

|
Найдем превышения для незаполненных клеток:
 ;
;  ;
;
 ;
;  .
.
Т.к.  , следовательно, исходное опорное решение оптимальным не является. Необходимо перейти к другому опорному решению. Для этого надо перераспределить грузы, перемещая их из занятых клеток в свободные. Для свободной клетки с
, следовательно, исходное опорное решение оптимальным не является. Необходимо перейти к другому опорному решению. Для этого надо перераспределить грузы, перемещая их из занятых клеток в свободные. Для свободной клетки с  строим цикл (замкнутая ломаная линия), все вершины которого кроме одной лежат в занятых клетках, углы прямые, число вершин четное. В свободной клетке цикла ставим знак «+», затем поочередно проставляем знаки «-» и «+». Из всех вершин со знаком
строим цикл (замкнутая ломаная линия), все вершины которого кроме одной лежат в занятых клетках, углы прямые, число вершин четное. В свободной клетке цикла ставим знак «+», затем поочередно проставляем знаки «-» и «+». Из всех вершин со знаком
«-» выбираем наименьший груз. В клетки со знаком «+» добавляем этот груз, а у клеток со знаком «-» отнимают этот груз. В результате перераспределения груза получим новый опорный план. Полученное решение проверяем на оптимальность и т.д., пока не получим оптимальное решение. В нашем примере имеем  .
.


| 
| 
| 
|

| |

| 2 – | 2 + | |||

| 4 + | 5 – | |||

| |||||

| -2 |
 ;
;  ;
;  ;
;  .
.
 .
.


| 
| 
| 
|
| |

| 2 | 2 | -3 | ||

| 4 | 5 | |||

| -1 | ||||

|
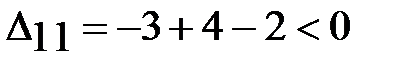 ;
;  ;
; 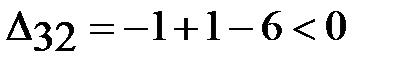 ;
; 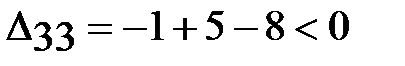 .
.
Т.к. все оценки свободных клеток отрицательны, следовательно, полученное решения является оптимальным.
 . При этом стоимость транспортных расходов равна
. При этом стоимость транспортных расходов равна 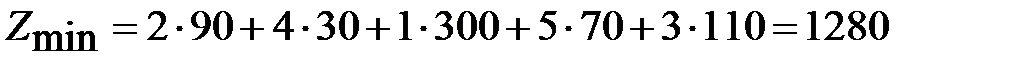 (усл. ден.ед.). По сравнению с исходным планом стоимость уменьшилась на 1610–1280=330 усл.ден.ед. Мы рассмотрели задачу закрытого типа и имеющую невырожденное решение. При решении транспортных задач может оказаться, что число занятых клеток меньше, чем m+n-1, тогда задача имеет вырожденное решение. Для ее решения необходимо в свободную клетку с наименьшим тарифом ввести нулевую поставку. При открытой ТЗ
(усл. ден.ед.). По сравнению с исходным планом стоимость уменьшилась на 1610–1280=330 усл.ден.ед. Мы рассмотрели задачу закрытого типа и имеющую невырожденное решение. При решении транспортных задач может оказаться, что число занятых клеток меньше, чем m+n-1, тогда задача имеет вырожденное решение. Для ее решения необходимо в свободную клетку с наименьшим тарифом ввести нулевую поставку. При открытой ТЗ 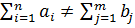 , необходимо ввести фиктивного потребителя, если
, необходимо ввести фиктивного потребителя, если  или фиктивного поставщика, если
или фиктивного поставщика, если  . Для ТЗ также можно дать экономический анализ. А также отметим, что алгоритм и методы решения ТЗ могут быть использованы при решении некоторых экономических задач, не имеющих ничего общего с транспортировкой груза. В этом случае величины тарифов
. Для ТЗ также можно дать экономический анализ. А также отметим, что алгоритм и методы решения ТЗ могут быть использованы при решении некоторых экономических задач, не имеющих ничего общего с транспортировкой груза. В этом случае величины тарифов  имеют различный смысл в зависимости от конкретной экономической задачи. Например: 1) оптимальное закрепление за станками операций по обработке деталей; 2) увеличение производительности автомобильного транспорта за счет минимизации порожнего пробега и т.д.
имеют различный смысл в зависимости от конкретной экономической задачи. Например: 1) оптимальное закрепление за станками операций по обработке деталей; 2) увеличение производительности автомобильного транспорта за счет минимизации порожнего пробега и т.д.
|
|
|


