11.4. Экспериментальное подтверждение молекулярно-кинетической теории газов (опыт Штерна)

11. 4. Экспериментальное подтверждение молекулярно-кинетической теории газов (опыт Штерна)

В 1920 г. Штерн поставил опыт, с помощью которого можно было непосредственно проверить теорию распределения молекул по скоростям и измерить скорость теплового движения молекул. Суть опыта поясняется рис. 11. 5.

Два коаксиальных цилиндра вращаются как единое целое с угловой скоростью w. По оси натянута платиновая проволока, покрытая тонким слоем серебра. Провод нагревается электрическим током. Температура проводки измеряется по ее электрическому сопротивлению. При температуре t = 1200⁰С атомы серебра испаряются и разлетаются по всем направлениям. Через узкую щель, прорезанную во внутреннем цилиндре, вылетает пучок атомов серебра, скорость которых направлена вдоль радиусов.

Пока атом, летящий со скоростью v, проходит расстояние между цилиндрами l, цилиндры успевают повернуться на угол Dj, , но , следовательно,

, при l » R.

Откуда

,

где DS – расстояние по окружности внешнего цилиндра от конца радиуса, проведенного через отверстие (через границу щели).

Вычисленные по результатам эксперимента значения скорости оказались близки к теоретическим результатам; кроме того, профиль сечения слоя серебра, как показано на рисунке, весьма точно соответствует распределению Максвелла молекул по скоростям. Теория получила хорошее подтверждение на опыте.

Лекция 12. Некоторые вопросы статистической физики

Распределение энергии по степеням свободы. Вероятность и флюктуации. Распределение молекул /частиц/ по абсолютным значениям скорости. Распределение Максвелла. Скорости теплового движения частиц. Средняя длина свободного пробега молекул. Распределение Больцмана. Барометрическая формула. Внутренняя энергия и теплоемкости идеального газа. Классическая теория теплоемкостей.

12. 1. Распределение энергии по степеням свободы

Выражение для средней энергии молекулы газа 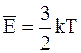 учитывает только её среднюю энергию поступательного движения. Но наряду с поступательным движением, молекула может вращаться и совершать колебания. Эти виды движения так же связаны с некоторым запасом энергии, определить который, можно пользуясь понятием статистической физики о равном распределении энергии по степеням свободы.

Число независимых координат, необходимых для полного описания положения системы в пространстве, называется числом степеней свободы (i).

Так, например, движение точки, совершающей перемещение по всей области пространства в любой момент времени будет полностью описано тремя координатами, т. е. она обладает тремя степенями свободы (i=3).

Если на характер изучаемого движения накладывать некоторые ограничения, то число степеней свободы уменьшается.

Так для описания движения точки по поверхности необходимо задать две независимые координаты, т. е. движущаяся по поверхности точка имеет две степени свободы (i = 2).

Точка, совершающая движение по прямой, имеет одну степень свободы (i = 1). В общем случае точка или система точек наряду с поступательным движением может одновременно участвовать во вращательном и колебательном движениях. Общее число степеней свободы в этом случае будет равно

                                     (12. 1)

где i_п - число степеней свободы поступательного движения точки;

i_вр - число степеней свободы вращательного движения точки;

i_к - число степеней свободы колебательного движения точки ( );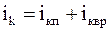

i_кп - число степеней свободы колебаний точки при поступательном движении;

i_квр - число степеней свободы колебаний точки при вращательном движении.

По аналогии с механическими системами, каждой молекуле, каждому атому газа можно приписать определённое число степеней свободы, рассматривая при этом их как материальные точки. Так, одноатомная молекула газа имеет только три степени свободы поступательного движения (i = 3); двухатомная при упругой связи – шесть степеней свободы (i = 6), а при жёсткой связи - пять степеней свободы (i = 5); трёхатомная молекула при жёсткой связи между атомами имеет шесть степеней свободы (i = 6).

Известно, что средняя кинетическая энергия поступательного движения молекул равна

Поступательное движение описывается тремя степенями свободы, а т. к. все степени свободы равноправны, то на каждую из них приходится

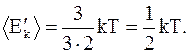                         (12. 2)

Но ни один из видов движения (поступательное, вращательное, колебательное) не имеет преимуществ перед другими. Следовательно, можно утверждать: «На любую степень свободы приходится в среднем одинаковая энергия, а молекула, обладающая i степенями свободы, будет обладать энергией 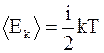». Данное утверждение называют теоремой о равномерном распределении энергии по степеням свободы (теорема Больцмана).

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: