12.4. Внутренняя энергия и теплоемкости идеального газа. Классическая теория теплоемкостей

12. 2. Вероятность и флюктуации. Распределение молекул (частиц) по абсолютным значениям скорости. Распределение Максвелла. Скорости теплового движения частиц. Средняя длина свободного пробега молекул

Статистическая физика это раздел молекулярной физики, в котором изучаются свойства и движения не отдельных молекул (частиц), а совокупности частиц, характеризующиеся средними величинами.

Статистические закономерности - количественные закономерности, устанавливаемые статистическим методом, в котором рассматриваются лишь средние значения величин, характеризующих данную совокупность молекул (рассматривается конкретная молекулярная модель и к ней, применяются математические методы статистики, основанные на теории вероятностей).

Одними из основных понятий статистической физики являются: вероятность и флуктуации.

Вероятность это число способов, которыми может быть реализовано данное состояние макроскопической физической системы (предел, к которому стремится относительная частота появления некоторого события при достаточно большом, стремящемся к бесконечности числе повторений опыта при неизменных внешних условиях):

w = n/N,                                       (12. 3)

где N - число опытов;

n - число раз получено определенное событие.

Флуктуации это случайные отклонения физических величин от их среднего значения.

Согласно молекулярно-кинетической теории молекулы идеального газа находятся в непрерывном хаотическом движении с равномерным распределением по направлениям. Скорости молекул при этом изменяются по величине. Наиболее близкой к истинному значению скорости является средняя квадратичная скорость молекул, которая для газа массой " m" находящегося в состоянии равновесия, при T = const, остаётся постоянной

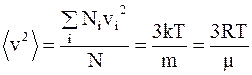 или , (12. 4)

где N_i - число молекул, обладающих скоростью v_i;

N - число всех молекул.

Рассчитаем среднюю квадратичную скорость молекул воздуха при температуре 300К (27⁰С). Будем считать, что воздух состоит из молекул азота (N₂) с молярной массой 28 кг/кмоль, тогда

м/с.

Постоянство < v_кв> объясняется тем, что в стационарном состоянии газа устанавливается стационарное распределение молекул по скоростям, подчиняющееся статистическому закону Максвелла.

Этот закон указывает на существование некоторой наиболее вероятной скорости движения молекул, в окрестности, которой в интервале (v + dv) находится большее число молекул, чем в окрестности другой скорости.

Возможные скорости движения молекул, заключенные в пределах от нуля до бесконечности, не равновероятны. Слишком большие по сравнению со средним квадратичным значением скорости могут реализоваться крайне редко, т. к. для этого должно реализоваться маловероятное явление, когда в результате случайных столкновений молекулы полностью передадут свою энергию одной (или нескольким) молекуле. Точно также практически исключено, что в результате соударений скорость молекулы станет равной нулю. Следовательно, очень малые и очень большие по сравнению со средним значением скорости маловероятны.

Из сказанного следует, что скорости молекул группируются в основном вблизи некоторого наиболее вероятного значения. Впервые функцию распределения молекул по скоростям получил Максвелл в 1860г. Мы воспользуемся готовым результатом и проанализируем его.

Пусть  - общее число молекул, заполняющих сосуд, 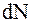 - число молекул, скорости которых заключены в интервале от v до v+dv. Естественно считать, что  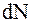прямо пропорционально общему числу частиц  и ширине интервала скоростей dv, т. е.

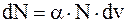                                      (12. 5)

При этом коэффициент пропорциональности a должен зависеть от v, т. е. a= f(v). Максвелл получил

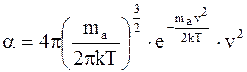.                (12. 6)

Подставляя (12. 6) в (12. 5) и разделив, обе части равенства, на dv получим

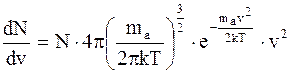.              (12. 7)

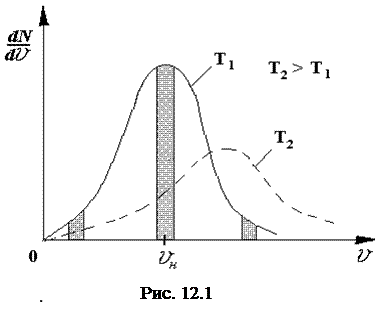На рисунке 12. 1 приведен график зависимости  для двух температур.

Проанализируем эту зависимость. Зависимость имеет выраженный максимум, в точке v = v_н. Значение v_н называют наивероятнейшей скоростью. Если выделить три одинаковых по ширине интервала скоростей в области малых скоростей, в окрестности наивероятнейшей скорости и в области больших скоростей, как показано на рисунке, то можно сделать следующие выводы:

1. Число молекул, имеющих малые скорости, относительно мало.

2. Число молекул, имеющих очень большие скорости, относительно мало.

3. Большая часть молекул движется со скоростями, близкими к наивероятнейшей.

Неожиданным оказывается ответ на вопрос - сколько же молекул имеют вполне определенное значение скорости, например, имеют наивероятнейшую скорость? Ответ – нисколько, нуль!!! Действительно, поскольку ширина заданного интервала скоростей равна нулю, то площадь соответствующей полоски на графике также равна нулю. Т. е., в большой массе молекул, в данное мгновение может не найтись ни одной молекулы, имеющей скорость с точно заданным значением.

Найдем значение наивероятнейшей скорости, для чего исследуем функцию  на экстремум. Возьмем от функции dN/dv производную по v и приравняем ее нулю: 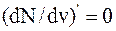. Для упрощения операции обозначим постоянный множитель буквой А, т. е.

.                            (12. 8)

Тогда

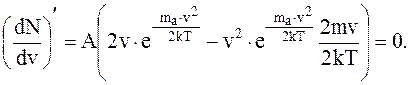    (12. 9)

Откуда

.              (12. 10)

Таким образом, получаем .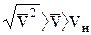

Из выражений (12. 10) видно, что с повышением температуры Т максимум исследуемой зависимости смещается вправо (рис. 12. 1). Вместе с тем максимум становится ниже. Это объясняется просто: если максимум сместился вправо, то кривая  становится шире, но площадь фигуры, образованной кривой  и осью «O - v» – должна быть одинаковой при Т₁ и T₂, т. к. указанные площади численно равны одной и той же величине - числу молекул внутри сосуда. Поэтому максимум для кривой  при T₂ должен быть ниже чем максимум этой кривой для Т₁.

По своему численному значению наивероятнейшая скорость близка к средней квадратичной скорости, характеризуется аналогичной зависимостью от температуры.

Молекулы газа, находясь в тепловом движении, непрерывно сталкиваются друг с другом. Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d. Эффективный диаметр несколько уменьшается при увеличении скорости молекул, т. е. с повышением температуры. Величина  называется эффективным сечением молекулы.

Средний путь, проходимый молекулой между двумя последовательными столкновениями, называется средней длиной свободного пробега < l>.

За 1 с молекула проходит в среднем путь, равный средней скорости . Если за 1 с в среднем происходит 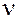столкновений, то средняя длина пробега

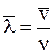.                                           (12. 11)

Предположим, что все молекулы, кроме данной молекулы, застыли неподвижно на своих местах (рис. 12. 2).

Столкновение происходит в том случае, если центр молекулы, с которой сталкивается данная молекула, лежит внутри цилиндра радиуса d. За 1 с данная молекула столкнется с неподвижными молекулами столько раз, сколько находится внутри такого цилиндра длиной l = │ v│ ∙ 1 c. Объем этого цилиндра составляет V = ; число молекул, заключенных в нем N =  (n – концентрация), следовательно, число столкновений

.                           (12. 12)

В действительности все молекулы движутся, вследствие чего число соударений определяется средней скоростью движения молекул по отношению друг к другу. Как показывает расчет, средняя скорость относительного движения молекул в 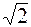 раз больше │ v│ (относительно стенок сосуда). Поэтому

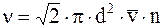                               (12. 13)

Подставляя (12. 13) в (12. 11), получим

 или .                 (12. 14)

Поскольку, при постоянной температуре, n изменяется пропорционально p(p = n∙ k∙ T), то

                                             (12. 15)

Так, например, при нормальных условиях n = 2, 68× 10²⁵ м ˉ ³, эффективный диаметр молекулы ~1 Å = 10^-10 м, поэтому длина свободного пробега l₀ = 2× 10^-7 м, а при давлении 0, 1 Па l~0, 10 м.

Учёт взаимодействия между молекулами показывает, что при возрастании температуры средняя длина свободного пробега несколько увеличивается. Средняя длина свободного пробега при какой-то температуре Т может быть определена по формуле

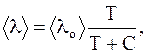                             (12. 16)

где C - постоянная Сезерленда, зависящая от интенсивности молекулярных взаимодействий.

< l_o> - длина свободного пробега молекул без учёта их взаимодействий.

Средняя длина свободного пробега молекул играет большую роль при молекулярно-кинетическом объяснении явлений переноса.

12. 3. Распределение Больцмана. Барометрическая формула

Атмосферное давление на какой-либо высоте обусловлено весом вышележащих слоев газа.

Если давление газа на высоте h_o равно p_o, а высоте h - p, то разность давлений с изменением высоты на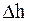

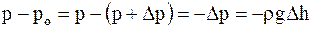 или 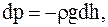 но r = m/V, а pV = (m/m)× RT, т. е. r = mp/RT, тогда

.         (12. 17)

При T = const, будем иметь

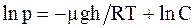 или                   (12. 18)

но при h = 0, p = p₀, C = p₀, следовательно

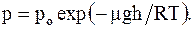                        (12. 19)

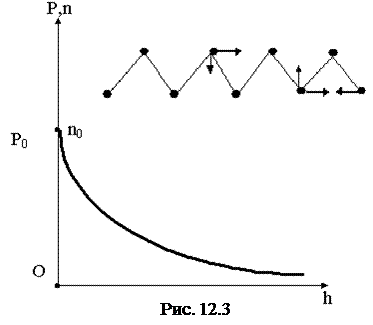Полученное соотношение называют барометрической формулой, которая показывает, что давление убывает с высотой тем быстрее, чем тяжелее газ и чем ниже его температура (рис. 12. 3).

Из молекулярно-кинетической теории известно, что 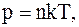 следовательно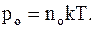

Заменив в барометрической формуле значения давлений, на число молекул в единице объема, с учетом того, что m/R = m/k, получим

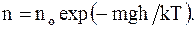                      (12. 20)

Формула (12. 20)определяет закон распределения молекул газа по высоте в поле сил тяготения.

Так как mgh = W_p (потенциальная энергия молекул в поле сил тяготения), то

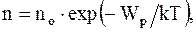                                 (12. 21)

где n_o - число молекул в единице объема в том месте, где потенциальная энергия молекул равна нулю;

n - число молекул в единице объема в тех точках пространства, где потенциальная энергия молекул равна W_p.

Из полученной формулы видно, что с понижением температуры, число молекул на высотах h не равных нулю, убывает и при T®0, оно равно нулю. Таким образом, при температуре T = 0 все молекулы газа расположились бы у поверхности Земли. При T®¥, n слабо убывает с высотой, так что все молекулы оказываются почти равномерно распределенными по высоте. Молекулы располагаются с большей плотностью там, где меньше их потенциальная энергия, и, наоборот, с меньшей плотностью там, где их потенциальная энергия больше. Отсюда

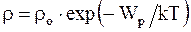; , (12. 22)

где m_o - масса одной молекулы.

Больцман показал, что такое распределение молекул справедливо не только в случае потенциального поля тяготения Земли, но и в любом силовом потенциальном поле. Это распределение и называют распределением Больцмана, которое дает распределение частиц по значениям потенциальной энергии.

Распределение частиц по значениям потенциальной энергии было использовано Перреном для экспериментального определения числа Авогадро.

 

12. 4. Внутренняя энергия и теплоемкости идеального газа. Классическая теория теплоемкостей

Внутренняя энергия тела 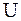 равна сумме кинетической энергии поступательного и вращательного движения молекул этого тела, и потенциальной энергии их взаимного расположения

.                         (12. 23)

Внутренняя энергия газа складывается из энергии отдельных молекул. В одном киломоле любого газа содержится N_А молекул (N_А - число Авогадро). Следовательно, один киломоль идеального газа имеет внутреннюю энергию, равную

              (12. 24)

Внутренняя энергия произвольной массы газа m

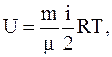                               (12. 25)

где m - молярная масса газа.

Таким образом, внутренняя энергия идеального газа зависит только от его объёма и давления.

Пользуясь понятием внутренней энергии газа, найдём выражение для его теплоёмкостей.

Теплоемкость это физическая величина, численно равная количеству теплоты, которое необходимо сообщить веществу для нагревания его на один градус.

Удельной теплоёмкостью " c" газа называется физическая величина, численно равная количеству теплоты, которое необходимо сообщить единице массы газа для нагревания её на один градус.

Кроме удельной теплоёмкости для газов вводится понятие молярной теплоёмкости.

Молярной теплоёмкостью " C" называется физическая величина, численно равная количеству теплоты, которое необходимо сообщить одному молю газа, чтобы увеличить его температуру на один градус

                                      (12. 26)

Для газов вводятся в рассмотрение молярные теплоемкости при постоянном объёме " C_v" и при постоянном давлении " C_p".

Если газ нагревается при постоянном объёме, то подводимое к газу тепло идёт на увеличение его внутренней энергии. Следовательно, в этом случае изменение внутренней энергии газа при нагревании его на один градус будет равно молярной теплоёмкости

, т. е. 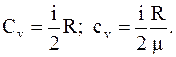    (12. 27)

Таким образом, для определения C_v необходимо знать число степеней свободы молекул газа.

При нагревании одного моля газа в условиях постоянного давления сообщаемое ему извне тепло идёт не только на увеличение его внутренней энергии, но и на совершение работы против внешних сил. Следовательно,

                               (12. 28)

Работа, совершаемая по свободному расширению одного моля газа в цилиндре под поршнем равна

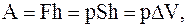                         (12. 29)

где S h = DV - увеличение первоначального объёма при нагревании газа на один градус (DV = V₂ - V₁).

На основании уравнения Менделеева - Клапейрона для одного моля идеального газа .

В нашем случае, 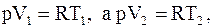 где T₂ = T₁ + 1, т. е.  откуда  Тогда , следовательно

 или .            (12. 30)

Так как c_p = c_v + R/m, то

.                                 (12. 31)

Очень часто для характеристики газа пользуются отношением

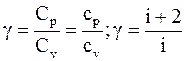.                          (12. 32)

Согласно многочисленным исследованиям по определению C_p, и C_v между теорией и экспериментом для одноатомных и двухатомных молекул имеется удовлетворительное совпадение. Согласно рассмотренной нами теории теплоёмкости газов должны быть целыми и кратными R/2. Однако, между теоретическими и экспериментальными данными имеется определённое расхождение.

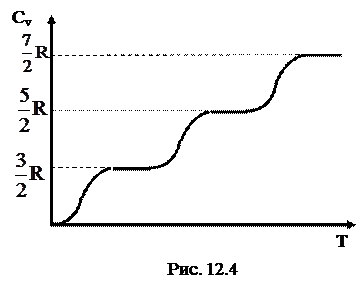Особенно большие расхождения между теорией и экспериментом наблюдаются при рассмотрении температурной зависимости теплоёмкости. Согласно изложенной теории теплоёмкость не должна зависеть от температуры; на самом же деле это оказывается справедливым только в определённых интервалах температур, при этом, в различных интервалах теплоёмкость имеет значения, соответствующее различному числу степеней свободы (рис. 12. 4, 12. 5).

Это связано с тем, что число степеней свободы одного и того же газа изменяется с изменением температуры. При низких температурах молекулы газа обладают только поступательными степенями свободы, при средних температурах - поступательными и вращательными степенями свободы, а при высоких температурах - поступательными, вращательными и колебательными степенями свободы. При этом, переход от одного числа степеней свободы к их другому числу осуществляется скачкообразно. Изменение числа степеней свободы приводит к изменению теплоемкостей газа. Такое поведение теплоёмкостей объясняется квантовой теорией. Согласно этому объяснению энергия вращательного и колебательного движений изменяются скачкообразно - квантуется, а энергия поступательного движения нет.

Молекулы газа, вернее подавляющая их часть, имеют энергию близкую по своему значению к средней кинетической энергии поступательного движения (< Е_к> ). Незначительная часть их имеет энергию, значительно превышающую < Е_к>. При низких температурах молекулы газа практически движутся поступательно, поэтому теплоёмкость газа равна 3R/2.

Повышение температуры сопровождается увеличением < Е_к> в результате чего всё большее и большее число молекул вовлекается во вращательное движение и при некоторой температуре, (вернее, в определённом интервале температур) все молекулы будут вращаться. Это соответствует увеличению их теплоёмкости до 5R/2. Наконец, при дальнейшем увеличении температуры часть молекул начинает совершать колебательное движение, в связи, с чем теплоёмкость станет равной 7R/2.

Таким образом, классическая теория теплоёмкостей верна только для отдельных температурных интервалов, при этом, каждому интервалу соответствует своё число степеней свободы.

Формулы кинетической энергии молекул газа и молярных теплоемкостей в классической теории теплоемкости, основанной на теореме Больцмана о равномерном распределении энергии по степеням свободы, представлены в таблицах 12. 1 и 12. 2.

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: