 |
Список рекомендуемой основной и дополнительной литературы
|
|
|
|
1.Вербицкий В. А. Математика в экономике (сборник задач): учеб. пособие / В. А. Вербицкий [и др.] – Хабаровск: РИЦ ХГАЭП, 1999. – 84 с.
2.Кремер Н. Ш. Высшая математика для экономистов: учебник для вузов/ Н. Ш. Кремер [и др.] – 2-е изд., перераб. и доп. – М.: ЮНИТИ, 2007. – 471 с.
3.Гусак А. А. Высшая математика: в 2 т.: учебник для вузов. – 2-е изд. испр. / А. А. Гусак. – Минск: ТетраСистемс, 2000. – 544 с.
4.Карасев А. И. Курс высшей математики для экономических вузов. Часть 1: учебник / А. И. Карасев, З. М. Аксютина, Т. К. Савельева ─ М.: Высшая школа, 1982. – 412 с.
5.Лихолетов И. И. Высшая математика, теория вероятностей и
математическая статистика: учебник / И. И. Лихолетов. ─ Минск: Вышейшая школа, 1976. – 724 с.
6.Математика для экономистов: задачник / кол. авторов под ред. С. И. Макарова, М. В. Мищенко. ─ М.: Кнорус, 2008. – 360 с.
7.Красс М.С. Основы математики и её приложения в экономическом образовании: учебник / М. С. Красс, Б. П. Чупрынов ─ 2-е изд. испр. ─ М: Дело, 2001. ─ 688 с.
8.Ломакина Е. Н., Математический анализ: Числовые последовательности и их приложения: учеб. пособие / Е. Н. Ломакина, М. Ф. Тиунчик ─ Хабаровск: ХГАЭП, 2008. – 104 с.
9.Макаров С.А. Математика для экономистов: учеб. пособие / С. А. Макаров ─ М.: Кнорус, 2007. – 264 с.
10.Кастрица О. А. Высшая математика для экономистов: учебник / О. А. Кастрица. ─ М: Новое знание, 2006. – 491 с.
11.Тиунчик М. Ф. Практикум по дифференциальным уравнениям: учеб. пособие / М. Ф. Тиунчик, Ю. Г. Саяпина. – Хабаровск: РИЦ ХГАЭП, 2010. – 92 с.
12.Тиунчик М. Ф. Математический анализ. Числовые ряды: учеб. пособие / М. Ф. Тиунчик, Е.О. Старкова, С. В. Тонконог – Хабаровск: РИЦ ХГАЭП, 2011. – 72 с.
13.Щипачев В. С. Высшая математика: учебник для вузов / В. С. Щипачев ─ 5-е изд. ─ М.: Высш. школа. 2001. ─ 479 с.
|
|
|
Контрольные задания, правила выполнения и оформления контрольных работ
Вариант для контрольной работы студент выбирает по двум последним цифрам своего номера зачётной книжки. Например: при номере зачётной книжки 952046, номер варианта 46. Номера заданий контрольной работы для каждого выбранного варианта указаны в таблице.
Таблица 1 ─ Варианты заданий
| Номера задач для контрольного задания | Номера задач для контрольного задания | |||||||||||||||
| Номер варианта | Задание 1 | Задание 2 | Задание 3 | Задание 4 | Задание 5 | Задание 6 | Задание 7 | Номер варианта | Задание 1 | Задание 2 | Задание 3 | Задание 4 | Задание 5 | Задание 6 | Задание 7 | |
| Задача | Задача | Задача | Задача | Задача | Задача | Задача | Задача | Задача | Задача | Задача | Задача | Задача | Задача | |||
|
|
|
|
|
|
При выполнении контрольной работы надо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студентам для переработки.
1. Контрольные работы можно выполнять либо в печатном варианте, либо в тетради пастой или чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.
2. На обложке тетради должны быть ясно написаны фамилия студента, его инициалы, номер зачётной книжки, название дисциплины и номер варианта контрольной работы.
3. В работу должны быть включены все задачи, указанные в задании, строго по своему варианту. Контрольные работы, содержащие не все задания, а также содержащие задачи не своего варианта, не зачитываются.
4. Решение задач надо располагать в порядке, указанном в заданиях, сохраняя номера задач.
5. Перед решением каждой задачи надо выписать полностью её
условие. Если несколько задач имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными из соответствующего номера.
6. В конце работы следует указать литературу, которую изучал студент, выполняя данную работу.
7. Студент должен подписать работу и поставить дату.
8. После получения отрецензированной работы (как зачтённой,
так и незачтённой) студент должен исправить в ней все отмеченные рецензентом ошибки и недочёты. В связи с этим следует оставлять в конце тетради чистые листы для работы над ошибками. Вносить исправления в сам текст работы после её рецензирования запрещается.
|
|
|
9. Если работа не допущена к защите, необходимо выполнить работу над ошибками и сдать на повторное рецензирование.
10.Зачтённые контрольные работы вместе с рецензиями обязательно предъявляются на зачёте и экзамене.
11.Перед сдачей зачёта и экзамена студент обязан защитить
контрольную работу.
Методические указания
Предел функции
Пусть функция 
ƒ(x) задана в некоторой окрестности точки х0.
Определение. Число А называется пределом функции f(x) в точке х0 если для любого, сколь угодно малого положительного числа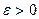 
найдётся такое положительное число δ>0, зависящее от ε, что для всех х, удовлетворяющих условию 0< 
, выполняется неравенство 
. Этот предел функции обозначается: 
или ƒ(х)→А при х→х0.
Практическое вычисление пределов основывается на следующих теоремах:
если существуют 
и 
, то
1) 
;
2) 
;
3) 
;
4) 
(при 
).
Определение. Функция α (х) называется бесконечно малой величиной при х→х0, или при х→∞, если её предел равен нулю 
Определение. Функция ƒ(х) называется бесконечно большой в точке х0 (или при х→х0), если имеет место одно из равенств: 
.
Теорема (о связи бесконечно большой и бесконечно малой функций): если ƒ(х) ─ бесконечно малая функция при х→х0, то 
─ бесконечно большая функция при х→х0, и наоборот.
Первый замечательный предел 
.
Второй замечательный предел 
.
Пример 1 
Поскольку функция непрерывна в точке х=7, искомый предел равен значению функции в этой точке. Используя теоремы о пределах суммы, разности, частного, получим
.
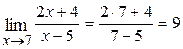Пример 2 
При х→5 числитель (2х + 5) стремится к 2 ∙ 5 + 5 = 15 (т.е. является ограниченной функцией), а знаменатель (х – 5) – к нулю (т.е. является бесконечно малой величиной), очевидно, их отношение есть величина бесконечно большая, т.е.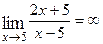 
.
В рассмотренных примерах предел находился сразу, чаще при вычислении пределов мы сталкиваемся с неопределённостями: 
, 
, 
, 
.
Пример 3
Пример 4
Пример 5 
.
Теорему о пределе частного здесь применить нельзя, так как числитель и знаменатель дроби конечного предела не имеют. В данном случае имеем неопределённость вида . Разделим числитель и знаменатель дроби на х в высшей степени (в данном случае на х2 ), а затем воспользуемся теоремами о пределах функций:
.
Здесь мы воспользовались теоремой о связи бесконечно большой и бесконечно малой функций: 
(a – любое число).
|
|
|
