 |
Общая схема исследования функции и построения графика
|
|
|
|
Для полного исследования функции и построения её графика рекомендуется использовать следующую схему:
1) найти область определения функции;
2) найти точки разрыва функции и вертикальные асимптоты (если они существуют);
3) исследовать поведение функции в бесконечности, найти горизонтальные и наклонные асимптоты;
4) исследовать функцию на чётность (нечётность) и на периодичность (для тригонометрических функций);
5) найти экстремумы и интервалы монотонности функции;
6) определить интервалы выпуклости и точки перегиба;
7) найти точки пересечения с осями координат, если возможно и некоторые дополнительные точки, уточняющие график.
Исследование функции проводится одновременно с построением её графика.
Пример 9 Исследовать функцию 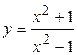 и построить график.
и построить график.
Решение:
1. Область определения:  ;
;
2. Функция терпит разрыв в точках  ,
,  ;
;
Исследуем функцию на наличие вертикальных асимптот.
 ;
; 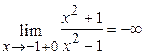 ,
,  ─ вертикальная асимптота.
─ вертикальная асимптота.
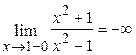 ;
;  ,
,  ─ вертикальная асимптота.
─ вертикальная асимптота.
3. Исследуем функцию на наличие наклонных и горизонтальных асимптот.
Прямая 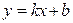 ─ наклонная асимптота, если
─ наклонная асимптота, если  ,
,  .
.
 ,
, 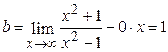 .
.
Прямая 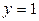 ─ горизонтальная асимптота.
─ горизонтальная асимптота.
4. Функция является четной т.к.  . Чётность функции указывает на симметричность графика относительно оси ординат.
. Чётность функции указывает на симметричность графика относительно оси ординат.
5. Найдём интервалы монотонности и экстремумы функции.
 .
.
Найдём критические точки, т.е. точки в которых производная равна 0 или не существует:  ;
; 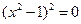 . Имеем три точки
. Имеем три точки  ;
; 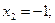
 . Эти точки разбивают всю действительную ось на четыре промежутка. Определим знаки
. Эти точки разбивают всю действительную ось на четыре промежутка. Определим знаки  на каждом из них.
на каждом из них.

На интервалах (-∞; -1) и (-1; 0) функция возрастает, на интервалах (0; 1) и (1; +∞) ─ убывает. При переходе через точку 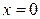 производная меняет знак с плюса на минус, следовательно, в этой точке функция имеет максимум
производная меняет знак с плюса на минус, следовательно, в этой точке функция имеет максимум  .
.
|
|
|
6. Найдём интервалы выпуклости, точки перегиба.

Найдём точки, в которых 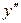 равна 0, или не существует.
равна 0, или не существует.
 не имеет действительных корней.
не имеет действительных корней. 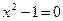 ,
,  ,
, 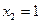
Точки  и
и 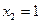 разбивают действительную ось на три интервала. Определим знак
разбивают действительную ось на три интервала. Определим знак 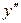 на каждом промежутке.
на каждом промежутке.

Таким образом, кривая на интервалах 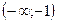 и
и  выпуклая вниз, на интервале (-1;1) выпуклая вверх; точек перегиба нет, т. к. функция в точках
выпуклая вниз, на интервале (-1;1) выпуклая вверх; точек перегиба нет, т. к. функция в точках  и
и 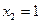 не определена.
не определена.
7. Найдем точки пересечения с осями.
С осью  график функции пересекается в точке (0; -1), а с осью
график функции пересекается в точке (0; -1), а с осью  график не пересекается, т.к. числитель данной функции не имеет действительных корней.
график не пересекается, т.к. числитель данной функции не имеет действительных корней.
График заданной функции изображён на рисунке 1.

Рисунок 1 ─ График функции 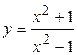
Применение понятия производной в экономике.
Эластичность функции
Для исследования экономических процессов и решения других прикладных задач часто используется понятие эластичности функции.
Определение. Эластичностью функции 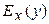 называется предел отношения относительного приращения функции
называется предел отношения относительного приращения функции  к относительному приращению переменной
к относительному приращению переменной  при
при  ,
,  . (VII)
. (VII)
Эластичность функции показывает приближённо, на сколько процентов изменится функция  при изменении независимой переменной
при изменении независимой переменной  на 1%.
на 1%.
Эластичность функции применяется при анализе спроса и потребления. Если эластичность спроса (по абсолютной величине)  , то спрос считают эластичным, если
, то спрос считают эластичным, если 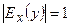 ─ нейтральным, если
─ нейтральным, если  ─ неэластичным относительно цены (или дохода).
─ неэластичным относительно цены (или дохода).
Пример 10 Рассчитать эластичность функции 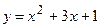 и найти значение показателя эластичности для
и найти значение показателя эластичности для 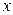 = 3.
= 3.
Решение: по формуле (VII) эластичность функции:
 .
.
Пусть х=3, тогда 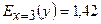 . Это означает, что если независимая переменная возрастёт на 1%, то значение зависимой переменной увеличится на 1,42 %.
. Это означает, что если независимая переменная возрастёт на 1%, то значение зависимой переменной увеличится на 1,42 %.
Пример 11 Пусть функция спроса  относительно цены
относительно цены  имеет вид
имеет вид 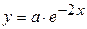 , где
, где 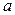 ─ постоянный коэффициент. Найти значение показателя эластичности функции спроса при цене х = 3 ден. ед.
─ постоянный коэффициент. Найти значение показателя эластичности функции спроса при цене х = 3 ден. ед.
|
|
|
Решение: рассчитаем эластичность функции спроса по формуле (VII)
 .
.
Полагая  ден.ед., получим
ден.ед., получим 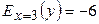 . Это означает, что при цене
. Это означает, что при цене  ден.ед. повышение цены на 1% вызовет снижение спроса на 6%, т.е. спрос эластичен.
ден.ед. повышение цены на 1% вызовет снижение спроса на 6%, т.е. спрос эластичен.
Интегралы
Определение. Функция F(x) называется первообразной функцией для функции ƒ(х) на промежутке X, если в каждой точке 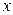 этого промежутка
этого промежутка
F/ (x) = f(x).
Если функция f(x) имеет первообразную F(x), то она имеет бесконечное множество первообразных, причём все первообразные содержатся в выражении F(x) + С, где С ─ произвольная постоянная.
Определение. Совокупность всех первообразных функции ƒ(х) на промежутке X называется неопределённым интегралом от функции f(x) и обозначается  т.е.
т.е. 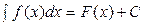 .
.
Свойства неопределённого интеграла
1.  ,
, 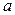 ─ постоянное число.
─ постоянное число.
2. 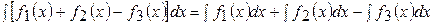 .
.
3.  .
.
4.  .
.
5.  .
.
Таблица основных интегралов
| № | Формулы | № | Формулы |

| 
| ||

| 
| ||
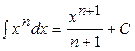 , , 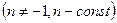
| 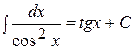
| ||
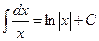
| 
| ||
 , , 
| 
| ||
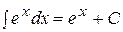
| 
| ||
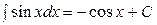
| 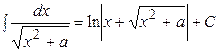
|
Пример 12 Найти интеграл  .
.
Решение:

Таблицу интегралов можно расширить, если применить формулы:
а)  , если
, если  ;
;
б) 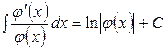 .
.
Пример 13 Найти интегралы.
а)  ; б)
; б)  ;
;
в)  ;
;
г) 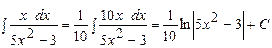 .
.
Замена переменной в неопределённом интеграле
(метод подстановки)
Одним из основных методов интегрирования является метод замены
переменной, описываемый следующей формулой:
 ,
,
где 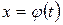 ─ функция, дифференцируемая на рассматриваемом промежутке.
─ функция, дифференцируемая на рассматриваемом промежутке.
Пример 14 Найти интегралы:
а) 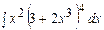 ; б)
; б)  ; в)
; в) 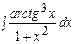 ; г)
; г)  .
.
Решение:
а)  ;
;
б)  ;
;
в) 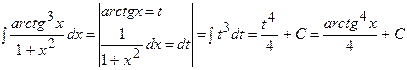 ;
;
г) 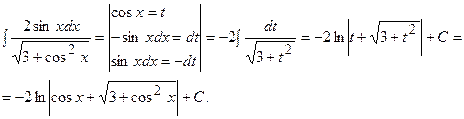
Интегрирование по частям
Интегрированием по частям называется нахождение интеграла по формуле
 ,
,
где  ─ непрерывно дифференцируемые функции.
─ непрерывно дифференцируемые функции.
При использовании этой формулы за U берётся та функция, которая при дифференцировании упрощается, а за dV ─ та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
Пример 15 Найти интегралы:
a)  ; б)
; б) 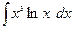 ; в)
; в) 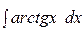 .
.
Решение:
a) 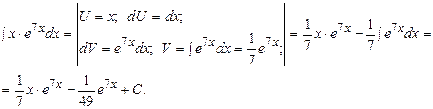
б) 
в) 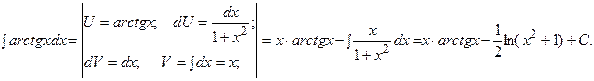
Формула Ньютона – Лейбница
Если функция f(x) непрерывна на отрезке [а;b] и F(x) ─ первообразная для f(x) на этом отрезке, то справедлива формула Ньютона ─ Лейбница
 .
.
Пример 16 Вычислить:  .
.
|
|
|
Решение:

Формула интегрирования по частям

Пример 17
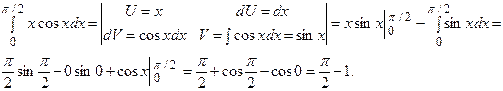
|
|
|


