Достаточные признаки сходимости числового ряда с положительными членами

Признак Даламбера. Пусть дан ряд (11) с положительными членами и существует конечный или бесконечный , тогда если , то ряд сходится, если 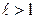, то ряд расходится, если ,то вопрос о сходимости ряда остается открытым.

 

Пример 29 Исследовать ряд на сходимость а) 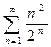б)

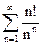
Решение: а) , ; ;

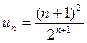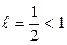по признаку Даламбера ряд сходится;

 

б) , . По признаку Даламбера

< 1, ряд сходится.

 

Замечание. Признак Даламбера применяется когда общий член ряда содержит выражение вида n! или а ⁿ.

Признак Коши. Пусть дан ряд (11) с положительными членами и существует конечный или бесконечный предел . Тогда, если , то ряд сходится, если 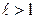, то ряд расходится, если ,то вопрос о сходимости ряда остается открытым.

Пример 30 а) б)

Решение. По признаку Коши.

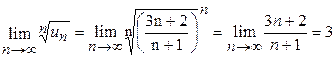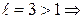а) = , ряд сходится. б) , ряд расходится.

Интегральный признак. Если члены знакоположительного ряда могут быть представлены, как числовые значения некоторой функции f(x): u₁=f(1), u₂=f(2), u₃=f(3),… и функция f(x) ─ непрерывная, монотонно убывающая на интервале (1; + ), то:

если 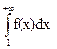сходится, то сходится и ряд (1);

если 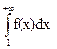расходится, то расходится так же и ряд (1).

Признак сравнения. Пусть даны два знакоположительных ряда и , для всех n выполняется неравенство _,

то если ряд сходится, то и ряд сходится,

если ряд расходится, то и ряд расходится.

Для сравнения часто используются «эталонные» ряды:

Геометрический ряд – сходится при , расходится при .

Гармонический ряд – расходится.

Обобщённый гармонический ряд ,сходится при 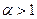, расходится при .

 

Знакочередующиеся ряды.

Определение. Знакочередующимся рядом называется ряд вида

u₁ - u₂ + u₃ - u₄ +…+(- 1 )ⁿ⁺¹u_n + … = . (12)

Признак Лейбница. Знакочередующийся ряд сходится, если выполняются два условия:

1)последовательность абсолютных величин членов ряда монотонно убывает, т.е.

2) общий член ряда стремится к нулю .

Пример 31 Исследовать ряд на сходимость .

Решение: Проверим выполнение условий признака Лейбница

1) ; ; 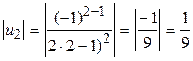члены ряда убывают по абсолютной величине.

2) 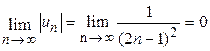, условия признака Лейбница выполняются, данный ряд сходится.

Пример 32 Исследовать сходимость ряда 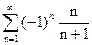. Решение: 1) ; ; 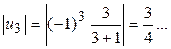члены ряда убывают по абсолютной величине;

2) 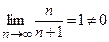, второе условие признака Лейбница не выполняется, ряд расходится.

 

 

Степенные ряды

Определение. Ряд вида a₀ + a₁x+ a₂x²+…+a_nx ⁿ_+… = – (13) называется степенным.

Числа a₀, a_1,… a_2, …a_n … называются коэффициентами ряда,

─ действительная переменная.

Теорема. Степенной ряд (13) сходится при значениях х, содержащихся в некотором интервале (-R, R) и расходится при значениях х вне этого интервала. Этот интервал называется интервалом сходимости, а число R ─ радиусом сходимости.

Формула для вычисления радиуса сходимости степенного ряда

(14)

Пример 33 Определить радиус сходимости степенного ряда и исследовать его сходимость на концах интервала .

Решение: Найдём коэффициенты

, Найдем ;

R =3, значит ряд сходится на интервале (-3; 3). Исследуем сходимость ряда на концах интервала.

При x = 3, получаем ряд , ряд расходится, как гармонический.

При x = -3, получаем знакочередующийся ряд , этот ряд сходится (по признаку Лейбница). Таким образом, ряд сходится для всех .

Пример 34 Найти область сходимости степенного ряда .

Найдём радиус сходимости , ,

 

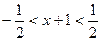, ─ интервал сходимости.

Исследуем сходимость ряда на концах интервала.

При , получим ряд

Для исследования ряда на сходимость воспользуемся интегральным признаком сходимости, в качестве функции f(x) возьмём функцию .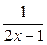

Несобственный интеграл расходится, следовательно и ряд расходится.

При получим ряд , по признаку Лейбница ряд сходится, таким образом, интервал сходимости .

⇐ Предыдущая1234

Поделиться:

Воспользуйтесь поиском по сайту: