 |
Стандартная ошибка регрессии Sxy.
|
|
|
|
Основные причины наличия в регрессионной модели случайного отклонения.
Невключение в модель всех объясняющих переменных.
Проблема в том, что никогда заранее не известно, какие факторы при создавшихся условиях действительно являются определяющими, а какими можно пренебречь. Здесь уместно отметить, что в ряде случаев учесть непосредственно какой-то фактор нельзя в силу невозможности получения по нему статистических данных.
Неправильный выбор функциональной формы модели.
Из-за слабой изученности исследуемого процесса либо из-за его переменчивости может быть неверно подобрана функция, его моделирующая. Это, безусловно, скажется на отклонении модели от реальности, что отразится на величине случайного члена.
Агрегирование переменных.
Во многих моделях рассматриваются зависимости между факторами, которые сами представляют сложную комбинацию других, более простых переменных.
Ошибки измерений.
Какой бы качественной ни была модель, ошибки измерений переменных отразятся на несоответствии модельных значений эмпирическим данным, что также отразится на величине случайного члена.
Ограниченность статистических данных.
Зачастую строятся модели, выражаемые непрерывными функциями. Но для этого используется набор данных, имеющих дискретную структуру. Это несоответствие находит свое выражение в случайном отклонении.
Непредсказуемость человеческого фактора.
Эта причина может «испортить» самую качественную модель. Действительно, при правильном выборе формы модели, скрупулезном подборе объясняющих переменных все равно невозможно спрогнозировать поведение каждого индивидуума.
Основные этапы регрессионного анализа.
|
|
|
1) выбор формулы уравнения регрессии;
2) определение параметров выбранного уравнения;
3) анализ качества уравнения и проверка адекватности уравнения эмпирическим данным, совершенствование уравнения.
Спецификация модели, каким образом она осуществляется?
Выбор формулы связи переменных называется спецификацией уравнения регрессии. В случае парной регрессии выбор формулы обычно осуществляется по графическому изображению реальных статистических данных в виде точек в декартовой системе координат, которое называется корреляционным полем (диаграммой рассеивания) (рис. 4.1).
На рис. 4.1 представлены три ситуации.
На графике 4.1, 
взаимосвязь между X и Y близка к линейной, и прямая 1 достаточно хорошо соответствует эмпирическим точкам. Поэтому в данном случае в качестве зависимости между X и Y целесообразно выбрать линейную функцию 
.
На графике 4.1, б реальная взаимосвязь между X и У, скорее всего, описывается квадратичной функцией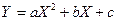 
(линия 2). И какую бы мы ни провели прямую (например, линия 1), отклонения точек наблюдений от нее будут существенными и неслучайными.
На графике 4.1, в явная взаимосвязь между X и У отсутствует. Какую бы мы ни выбрали форму связи, результаты ее спецификации и параметризации (определение коэффициентов уравнения) будут неудачными. В частности, прямые 1 и 2, проведенные
через центр «облака» наблюдений и имеющие противоположный наклон, одинаково плохи для того, чтобы делать выводы об ожидаемых значениях переменной У по значениям переменной X.
Стандартная ошибка регрессии Sxy.
Рассмотрим модель парной линейной регрессии
(5.1)
Пусть на основе выборки из 
наблюдений оценивается регрессия
(5.2)
Как показано в формуле (4.14), 
(5.3)
что означает, что коэффициент 
также является случайным. В самом деле, значение выборочной ковариации Sxy зависит от того, какие значения принимают X и У. Если X можно рассматривать как экзогенный фактор, значения которого известны, то значения У зависят от случайной составляющей 
. Теоретически коэффициент можно разложить на неслучайную и случайную составляющие.
|
|
|
Стандартная ошибка показывает отклонение эмпирического уравнения от теоретического. Чем меньше стандартная ошибка, тем лучше, т.е. эмпирическое уравнение близка к теоретическому. Мы знаем, что теоретическое уравнение используется для ген. совокупности, этот класс шире, а эмпирическое для конкретной выборки.
|
|
|
