Различие между теоретическим и эмпирическим уравнениями регрессии.

Линейная регрессия (теоретическое линейное уравнение регрессии) представляет собой линейную функцию между условным математическим ожиданием 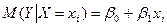зависимой переменной У и одной объ­ясняющей переменной X ( 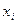— значения независимой перемен­ной в 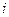-м наблюдении, .

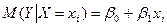(4.5)

Отметим, что принципиальной в данном случае является линейность по параметрам и .

Для отражения того факта, что каждое индивидуальное значение отклоняется от соответствующего условного мате­матического ожидания, необходимо ввести в соотношение (4.5) случайное слагаемое

(4.6)

Соотношение (4.6) называется теоретической линейной регрессионной моделью; и — теоретическими парамет­рами (теоретическими

коэффициентами) регрессии; — слу­чайным отклонением.

По выборке ограниченного объема мы сможем построить так называемое эмпирическое уравнение регрессии (4.8), где — оценка условного математического ожидания . и — оценки неизвестных параметров и , называе­мые эмпирическими коэффициентами регрессии. Следователь­но, в конкретном случае (4.9), отклонение — оценка теоретического случайного откло­нения .

В силу несовпадения статистической базы для генеральной совокупности и выборки оценки и практически всегда от­личаются от истинных значений коэффициентов и , что приводит к несовпадению эмпирической и теоретической линий регрессии. Различные выборки из одной и той же генеральной совокупности обычно приводят к определению отличающихся друг от друга оценок. Возможное соотношение между теоретическим и эмпирическим уравнениями регрессии схематично изображено на рис 4.3

задача состоит в том, чтобы по конкретной выборке , i = 1, 2,..., n, найти оценки и неизвестных параметров и , так, чтобы построенная линия регрессии являлась бы наилучшей в определенном смысле среди всех других прямых. Другими словами, построенная прямая должна быть «ближайшей» к точкам наблюдений по их совокупности.

 

Определение теоретической линейной регрессионной модели.

(4.6)

Соотношение (4.6) называется теоретической линейной регрессионной моделью; и — теоретическими парамет­рами (теоретическими коэффициентами) регрессии; — слу­чайным отклонением, зависимая переменная У и одна объ­ясняющая переменная X (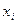 — значения независимой перемен­ной в 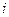-м наблюдении, .

 

Суть метода наименьших квадратов (МНК).

его суть состоит в минимизации суммы квадратов отклонений наблю­даемых значений зависимой переменной У от ее значений У, получаемых по уравнению регрессии.

 

Формулы расчета коэффициентов эмпирического парного линейного уравнения регрессии по МНК.

Пусть по выборке , i = 1, 2,..., n, требуется определить оценки и

эмпирического уравнения регрессии (4.8). В этом случае при использовании МНК минимизируется следующая функция (рис.4.4)

 

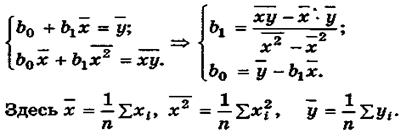
Доверительный интервал для условного математического ожидания зависимой переменной.

Одной из центральных задач эконометрического моделиро­вания является предсказание (прогнозирование) значений зависимой переменной при определенных значениях объясняющих переменных. Здесь возможен двоякий подход: либо предска­зать условное математическое ожидание зависимой переменной при определенных значениях объясняющих переменных (предска­зание среднего значения), либо прогнозировать некоторое конкретное значение зависимой переменной (предсказание конкретного значения).для имеет вид

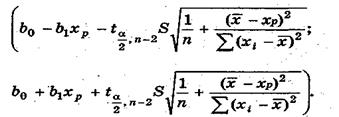
Для проверки гипотезы

используется статистика:

имеющая распределение Стьюдента с числом степеней свободы . Поэтому отклоняется, если

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: