Каким образом определяется модель множественной линейной регрессии?

модель множественной линейной регрессии.

Теоретическое линейное уравнение регрессии имеет вид:

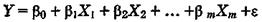
или для индивидуальных наблюдений i, i = 1, 2,…, n,

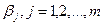Здесь — вектор размерности (т + 1) неиз­вестных параметров. , у = 1, 2,..., т, называется -м теорети­ческим коэффициентом регрессии (частичным коэффициентом регрессии). Он характеризует чувствительность величины Y к изменению 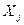. Другими словами, он отражает влияние на ус­ловное математическое ожидание M() зависи­мой переменной У объясняющей переменной Х_j при условии, что все другие объясняющие переменные модели остаются по­стоянными. — свободный член, определяющий значение У в случае, когда все объясняющие переменные X_j) равны нулю.

После выбора линейной функции в качестве модели зависи­мости необходимо оценить параметры регрессии.

Пусть имеется n наблюдений вектора объясняющих пере­менных X = (X₁, X₂,..., Х_т) и зависимой переменной У:

 

Для того чтобы однозначно можно было бы решить задачу отыскания параметров (т.е. найти некоторый наи­лучший вектор ), должно выполняться неравенство . Если это неравенство не будет выполняться, то существует бес­конечно много различных векторов параметров, при которых линейная формула связи между X и У будет абсолютно точно соответствовать имеющимся наблюдениям. При этом, если , то оценки коэффициентов вектора рассчитываются единственным образом — путем решения системы т + 1 линей­ного уравнения:

Например, для однозначного определения оценок парамет­ров уравнения регрессии достаточно иметь выборку из трех наблюдений (), i = 1, 2, 3. В этом случае найденные значения параметров 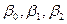опреде­ляют такую плоскость в трехмерном про­странстве, которая пройдет именно через имеющиеся три точ­ки. С другой стороны, добавление в выборку к имеющимся трем наблюдениям еще одного приведет к тому, что четвертая точка () практически наверняка будет лежать вне построенной плоскости (и, возможно, достаточно далеко). Это потребует определенной переоценки параметров.

Таким образом, вполне логичен следующий вывод: если чис­ло наблюдений больше минимально необходимого, т.е. n > m+1, то уже нельзя подобрать линейную форму, в точности удовлетво­ряющую всем наблюдениям, и возникает необходимость опти­мизации, т.е. оценивания параметров , при которых формула дает наилучшее приближение для имеющихся на­блюдений.

В данном случае число = n — т — 1 называется числом степеней свободы. Нетрудно заметить, что если число степеней свободы невелико, то статистическая надежность оцениваемой формулы невысока. Например, вероятность верного вывода (по­лучения более точных оценок) по трем наблюдениям сущест­венно ниже, чем по тридцати. Считается, что при оценивании множественной линейной регрессии для обеспечения статисти­ческой надежности требуется, чтобы число наблюдений по крайней мере в 3 раза превосходило число оцениваемых пара­метров.

Самым распространенным методом оценки параметров уравнения множественной линейной регрессии является ме­тод наименьших квадратов (МНК). Напомним, что его суть состоит в минимизации суммы квадратов отклонений наблю­даемых значений зависимой переменной У от ее значений У, получаемых по уравнению регрессии.

 

Предпосылки МНК. Каковы последствия их невыполнимости?

Предпосылки МНК

1°. Математическое ожидание случайного отклонения равно нулю для всех наблюдений:

M() = 0, i = 1, 2,..., п.

2°.Гомоскедастичностъ (постоянство дисперсии откло­нений). Дисперсия случайных отклонений < постоянна:

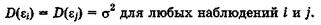
3°. Отсутствие автокорреляции.

Случайные отклонения и - являются независимыми друг от друга для всех

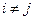
4°. Случайное отклонение должно быть независимо от объясняющих переменных.

5°. Модель является линейной относительно параметров.. Для случая ножественной линейной регрессии сущест­венными являются еще две предпосылки.

6°. Отсутствие мультиколлинеарности.

Между объясняющими переменными отсутствует строгая (сильная) линейная зависимость.

7°. Ошибки , i = 1, 2,..., n, имеют нормальное распределе­ние (.

Выполнимость данной предпосылки важна для проверки статистических гипотез и построения интервальных оценок.

При невыполнимости данной предпосылки (при гетероске­дастичности) последствия применения МНК будут следующи­ми.

Оценки коэффициентов по-прежнему останутся несме­щенными и линейными.

1. Оценки не будут эффективными (т.е. они не будут иметь наименьшую дисперсию по сравнению с другими оценками дан­ного параметра). Они не будут даже асимптотически эффектив­ными. Увеличение дисперсии оценок снижает вероятность по­лучения максимально точных оценок.

2. Дисперсии оценок будут рассчитываться со смещением. Смещенность появляется вследствие того, что не объясненная

уравнением регрессии дисперсия (т - число объ ясняющих переменных), которая используется при вычисле­нии оценок дисперсий всех коэффициентов (формула (6.23)), не является более несмещенной.

4. Вследствие вышесказанного все выводы, получаемые на основе соответствующих t- и F-статистик, а также интервальные оценки будут ненадежными. Следовательно,статистические выводы, получаемые при стандартных проверках качества оценок, могут быть ошибочными и приводить к неверным за­ иключениям по построенной модели. Вполне вероятно, что стан­дартные ошибки коэффициентов будут занижены, а следова­тельно, t-статистики будут завышены. Это может привести к признанию статистически значимыми коэффициентов, таковы­ми на самом деле не являющихся.

 

1. 13)Характеристика коэффициентов уравнения регрессии. С помощью т статистики, Р, грубое правило

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: