 |
Сила давления жидкости на плоскую стенку
|
|
|
|
Рассмотрим произвольную площадку ds, расположенную на плоской наклонной стенке сосуда с жидкостью на расстоянии Y от оси X, и определим силы, действующие на эту площадку. Сила от давления, действующего на элементарную площадку dS, будет описываться формулой:
Если проинтегрировать это выражение по площади, можно определить полную силу, действующую на всю площадь целиком
Из рисунка ясно, что в последнем выражении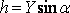 
. Подставив значение h в предыдущее выражение, будем иметь:
Из теоретической механики известно, что интеграл 
есть ни что иное, как статический момент площади Sотносительно оси 0X. Он равен произведению этой площади на координату её центра тяжести, т.е. можно записать
где Yс – расстояние от оси X до центра тяжести площади S.
Подставив формулу момента в выражение силы, получим:
Анализ второго слагаемого показывает, что произведение 
это глубина положения центра тяжести площадки, а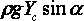 
- избыточное давление жидкости в центре тяжести площадки. С учётом этого можно записать
Сумма в скобках в последнем выражении является абсолютным давлением в центре тяжести рассматриваемой произвольной площадки. Таким образом, можно сделать вывод: полная сила давления жидкости на плоскую стенку равна произведению её площади на величину гидростатического давления в центре тяжести этой стенки.
Однако необходимо учесть, что эта сила не сконцентрирована в точке, а распределена по площади. И распределение это неравномерно. По этой причине для расчётов, кроме величины силы действующей на наклонную площадку, необходимо знать точку приложения равнодействующей.
11. Сила давления ж-ти на циллиндрические и сферические пов-ти
|
|
|
Рассмотрим открытый сосуд, заполненный покоящейся жидкостью. Одна из стенок сосуда имеет цилиндрическое очертание.
(.) 0 – центр кривизны поверхности.
В соответствии с I свойством гидростатического давления в каждой точке такой поверхности давление направлено по нормали. Следовательно, в случае цилиндрической (и сферической) поверхности направление результирующей силы давления P всегда проходит через центр кривизны поверхности.
В общем случае криволинейной поверхности с несколькими центрами кривизны это не выполняется – через центр кривизны поверхности в данной точке проходит только направление элементарных составляющих сил.
Результирующую силу давления P можно разложить на две составляющие:
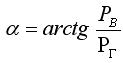
Таким образом, дя определения величины и направления силы P необходимо определить Рв и Pг. Найдём Рв и Pг.
Рис. 7.2. К определению величины силы давления на криволинейную поверхность
[1] Для этого выделим на рассматриваемой криволинейной поверхности элементарную площадку dw (Рис. 7.2). В связи с малостью её размеров её можно считать плоской. Центр площадки находится на глубине h.
[2] На эту площадку действует сила dP, обусловленная гидростатическим давлением в точке, соответствующей центру площадки. Как и ренее, пренебрегаем изменением давления при перемещении вдоль площадки в связи с малостью её размеров.
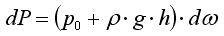
Горизонтальная составляющая силы dP
Из рисунка 7.2 видно, что
- вертикальная проекция площадки dw
Таким образом:
Проинтегрируем последнее выражение по площади w поверхности сосуда, для того чтобы получить величину горизонтальной составляющей силы давления на эту поверхность.
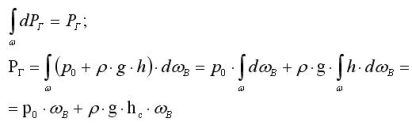
поскольку
- статический момент
вертикальной проекции площади dw относительно оси OX. (В данном случае ось OX направлена нормально к плоскости чертежа, она находится на прямой, образованной пересечением цилиндрической поверхности и плоскостью свободной поверхности жидкости).
|
|
|
hc – глубина погружения центра тяжести вертикальной проекции площади w.
- вертикальная проекция площади w (сумма вертикальных проекций элементарных площадок dwв).
Таким образом:
Это утверждение можно распространить и на случай других криволинейных поверхностей (нецилиндрических).
Вертикальная составляющая силы давления dP на элементарную площадку:
(*)
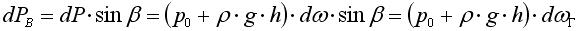аналогично 
- горизонтальная проекция площадки dw.
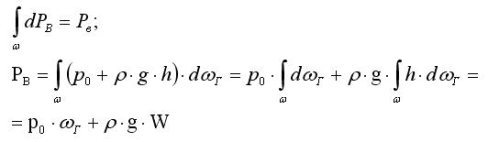Для определения величины вертикальной составляющей силы давления на рассматриваемую поверхность проинтегрируем (*) по площади w.
где
– объём жидкости, находящийся над элементарной площадкой dw;
– объём жидкости, находящийся над криволинейной поверхностью – объём тела давления;
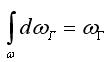– горизонтальная проекция площади криволинейной поверхности;
- вес тела давления.
Итак:
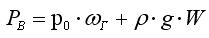
Это утверждение также можно распространить и на случай других криволинейных поверхностей (нецилиндрических).
Зависимости, полученные для величин горизонтальной и вертикальной составляющих силы гидростатического давления на криволинейные поверхности справедливы также и для плоских поверхностей.
В случае определения составляющих силы избыточного гидростатического давления при давлении на поверхности жидкости равном атмосферному, давление на поверхности жидкости следует принимать равным нулю.
Плавание тел
Плавание тел - состояние равновесия твёрдого тела, частично или полностью погруженного в жидкость (или газ). Основная задача теории П. т.— определение положений равновесия тела, погруженного в жидкость, выяснение условий устойчивости равновесия. Простейшие условия П. т. указывает Архимеда закон.
Основные понятия теории П. т. (рис. 1): 1) водоизмещение тела — вес жидкости, вытесняемой телом в состоянии равновесия (совпадает с весом тела); 2) плоскость возможной грузовой ватерлинии — всякая плоскость ab, отсекающая от тела объём, вес жидкости в котором равен водоизмещению тела; 3) поверхность грузовых ватерлиний — поверхность I, в каждой точке которой касательная плоскость является плоскостью возможной грузовой ватерлинии; 4) центр водоизмещения — центр тяжести А объёма, отсекаемого плоскостью возможной грузовой ватерлинии; 5) поверхность центров водоизмещения — поверхность II, являющаяся геометрическим местом центров водоизмещения.
|
|
|
Если тело погрузить в жидкость до какой-нибудь плоскости возможной грузовой ватерлинии ab (рис. 2), то на тело будут действовать направленная перпендикулярно этой плоскости, т. е. вертикально вверх, Поддерживающая сила F, проходящая через центр А, и численно равная ей сила тяжести р. Как доказывается в теории П. т., направление силы F совпадает одновременно с направлением нормали An к поверхности II в точке А.
В положении равновесия силы F и Р должны быть направлены вдоль одной прямой, т. е. нормаль к поверхности II, восстановленная из центра А, должна проходить через центр тяжести С тела (нормали A1C, A2C на рис. 1). Число нормалей к поверхности II, проходящих через центр тяжести С, даёт число возможных положений равновесия плавающего тела. Если тело вывести из положения равновесия, то на него будет действовать пара сил F, Р. Когда эта пара стремится вернуть тело в положение равновесия, равновесие устойчиво, в противном случае — неустойчиво. Об устойчивости равновесия можно судить по положению Метацентра. Другой простой признак: положение равновесия устойчиво, если для него расстояние между центрами А и С является наименьшим по сравнению с этим расстоянием для соседних положений (на рис. 1 при погружении до плоскости a2b2 равновесие устойчиво, а до a1b1 — неустойчиво).
Рис. 1. ab, a1b1, a2b2 — плоскости возможной грузовой ватерлинии; A, A1, A2 — центры водоизмещения для объёмов, отсекаемых плоскостями ab, a1b1, a2b2; I — поверхность грузовых ватерлиний; II — поверхность центров водоизмещения.
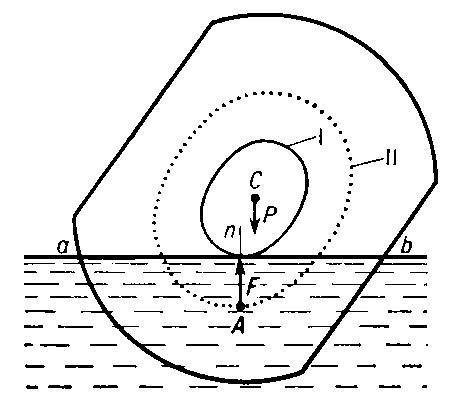
Рис. 2. Силы, действующие на тело, погруженное в жидкость до грузовой ватерлинии ab.
|
|
|
