Дифференциальные уравнения движения вязкой жидкости Навье-Стокса

Навье — Стокса уравнения, дифференциальные уравнения движения вязкой жидкости (газа). Названы по имени Л. Навье и Дж. Стокса. Для несжимаемой (плотность r = const) и ненагреваемой (температура Т = const) жидкости Н. — С. у. в проекциях на оси прямоугольной декартовой системы координат (система трёх уравнений) имеют вид:

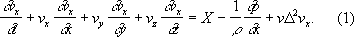
Здесь t — время, x, у, z — координаты жидкой частицы, vx, vy, vz — проекции её скорости, X, Y, Z — проекции объёмной силы, p — давление, v = m/r — кинематический коэффициент вязкости (m — динамический коэффициент вязкости),

Два других уравнения получаются заменой x на у, у на z и z на x. Н. — С. у. служат для определения vx, vy, vz, р как функций x, у, z, t. Чтобы замкнуть систему, к уравнениям (1) присоединяют уравнение неразрывности, имеющее для несжимаемой жидкости вид:

Для интегрирования уравнений (1), (2) требуется задать начальные (если движение не является стационарным) и граничные условия, которыми для вязкой жидкости являются условия прилипания к твёрдым стендам. В общем случае (движение сжимаемой и нагреваемой жидкости) в Н. — С. у. учитывается ещё переменность r и зависимость m от температуры, что изменяет вид уравнений. При этом дополнительно используются уравнение баланса энергии и Клапейрона уравнение.

Н. — С. у. применяют при изучении движений реальных жидкостей и газов, причём в большинстве конкретных задач ограничиваются отысканием тех или иных приближённых решений.

Уравнения Рейнольдса

Уравнения Рейнольдса (англ. RANS (Reynolds-averaged Navier-Stokes)) — уравнения Навье-Стокса (уравнения движения вязкой жидкости) осредненные по Рейнольдсу.

Используются для описания турбулентных течений. Метод осреднения Рейнольдса заключается в замене случайно изменяющихся характеристик потока (скорость, давление, плотность) суммами осредненных и пульсационных составляющих. В случае стационарного течения несжимаемой Ньютоновской жидкости уравнения Рейнольдса записываются в виде:

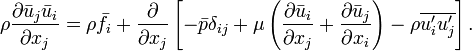
Переменные, осредненные по времени, отмечены в этом уравнении чертой сверху, а пульсационные составляющие — апострофом. Левая часть уравнения (нестационарный член) описывает изменение количества движения жидкого объёма, вследствие изменения во времени осредненной составляющей скорости. Это изменение компенсируется (см. правую часть уравнения) осредненными внешними силами , осредненными силами давления , вязкостными силами . Кроме того, в правую часть входят кажущиеся напряжения (напряжения Рейнольдса, турбулентные напряжения) , учитывающие дополнительные потери и перераспределение энергии в турбулентном потоке (по сравнению с ламинарным потоком).

Уравнения Рейнольдса описывают осредненное по времени течение жидкости, их особенность (по сравнению с исходными уравнениями Навье-Стокса) заключается в том, что в них появились новые неизвестные функции, которые характеризуют кажущиеся турбулентные напряжения. Система уравнений Рейнольдса содержит шесть неизвестных и оказывается незамкнутой, в связи с чем, для её решения приходится привлекать дополнительную информацию.

Весьма существенным является то обстоятельство, что напряжения Рейнольдса являются случайными величинами, поэтому в расчетах используют статистические данные об их величине (модели турбулентности), которые получают путём анализа результатов эксперимента. Также необходимо отметить, что напряжения Рейнольдса являются свойством течения (а не свойством жидкости), поэтому, если условия рассматриваемой задачи будут существенно отличаться условий, в которых были получены статистические данные о величине напряжений Рейнольдса, результаты расчёта могут оказаться качественно неверными. К настоящему времени разработано значительное количество моделей турбулентности различной сложности, позволяющих оценить (смоделировать) величину турбулентных напряжений в различных условиях.