 |
Свободные затухающие колебания
|
|
|
|
Если свободные колебания происходят в системе, в которой действует сила трения 
, где r – коэффициент трения (сопротивления среды), то уравнение (2) движения тела имеет вид:
, или 
, (22)
где коэффициент затухания
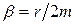, (23)
а собственная частота колебательной системы, т.е. та частота, с которой система совершала бы колебания в отсутствие трения:
. (24)
Решение уравнения (22) – функция
, (25)
представляющая собой уравнение свободных затухающих колебаний.
Частота затухающих колебаний
. (26)
Декрементом затухания называется величина, равна отношению амплитуд, соответствующих моментам времени, отличающимся на период:
. (27)
Логарифмический декремент затухания:
. (28)
Добротность колебательной системы:
. (29)
Время релаксации τ – время, за которое амплитуда убывает в е раз:
. (30)
Вынужденные колебания
Если система совершает колебания под внешним воздействием, изменяющимся периодически, то такие колебания называются вынужденными. Уравнение движения в этом случае имеет вид (2) 
. Введя обозначения (23) и (24), получим уравнение
, (31)
решение которого и есть уравнение вынужденных колебаний
, (32)
где 
– частота вынуждающей силы.
Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При приближении частоты вынуждающей силы (ω) к частоте собственных колебаний (ω 0) наблюдается резонанс – явление резкого возрастания амплитуды вынужденных колебаний. Амплитуда при резонансе
, (33)
а резонансная частота
. (34)
Упругие волны.
Волна – процесс распространения колебаний в упругой среде. Линия, указывающая направление распространения волны, называется лучом. Если колебания частиц среды происходят перпендикулярно лучу, то волна является поперечной. Если же частицы колеблются вдоль луча, то волна называется продольной.
|
|
|
Геометрическое место точек пространства, до которых дошел волновой процесс к данному моменту времени, называется фронтом волны. Волновой 
поверхностью называется геометрическое место точек, колеблющихся в одинаковой фазе. В то время как волновых поверхностей для данной волны можно провести сколь угодно много, волновой фронт один. Волна называется плоской, если волновые поверхности – плоскости, и сферической, если они являются сферами
Волновой фронт перемещается со скоростью 
(фазовая скорость) и за время, равное периоду Т колебаний частиц, проходит расстояние 
(длина волны).
, (35)
где 
– частота колебаний частиц.
Уравнение плоской бегущей волны:
, (36)
где 
– смещение колеблющейся точки; 
– циклическая частота; 
– волновой вектор, модуль которого 
, а направление перпендикулярно волновой поверхности.
Уравнение волны, распространяющейся вдоль оси х,имеет вид:
, (37)
Волновое уравнение, решением которого является уравнение волны (36), представляет собой дифференциальное уравнение вида:
, (38)
где 
– оператор Лапласа.
Для плоской волны (37), распространяющейся вдоль оси 
, волновое уравнение имеет вид:
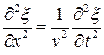, (39)
Разность фаз (
) колебаний двух точек, отстоящих от источника на расстояниях х 1 и х 2, соответственно, определяется из соотношения:
, (40)
где 
– разность хода двух волн.
Волновое движение сопровождается переносом энергии, которая складывается из кинетической энергии колеблющихся частиц и потенциальной энергии деформированных участков среды. Энергия, переносимая волной через некоторую поверхность в единицу времени, называется потоком энергии через эту поверхность. Плотностью потока энергии называется количество энергии 
, переносимое волной в среднем за единицу времени 
через единичную площадку (S), перпендикулярную направлению распространения волны:
|
|
|
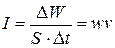, (41)
где 
– плотность энергии – средняя энергия частиц, содержащихся в единичном объеме.
Вектор Умова – вектор, направленный перпендикулярно фронту волны, указывающий направление распространения энергии и по модулю равный плотности потока энергии:
. (42)
Плотность энергии, представляющую собой энергию единицы объема, можно выразить через энергию каждой частицы и количество частиц n в единице объема:
, (43)
где 
– плотность среды.
Тогда 
интенсивность волны:
. (44)
Эффект Доплера: в случае движения источника и приемника волн относительно среды, в которой распространяется волна, частота, воспринимаемая приемником 
, и частота колебаний источника 
отличаются:
, (45)
где 
– скорость волн в среде, а 
– скорости движения приемника и источника, соответственно.
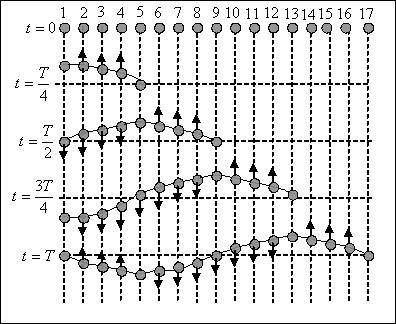
При одновременном распространении нескольких волн колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности, т.е., накладываясь, волны не возмущают друг друга (принцип суперпозиции). Если волны когерентны (имеют постоянную во времени разность фаз), то при их сложении наблюдается явление интерференции – перераспределение интенсивности волн, при котором в одних точках колебания усиливают друг друга, а в других – ослабляют. Если интерферируют две встречные плоские волны с одинаковой амплитудой и частотой, то возникающий при этом колебательный процесс называется стоячей волной. Уравнение стоячей волны:
. (46)
Выражение, стоящее в скобках, – амплитуда стоячей волны (как видно, зависящая от координаты).
Пучности наблюдаются в точках, координаты которых:
, 
, 
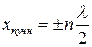, (47)
Уз лы наблюдаются в точках, координаты которых:
, 
. (48)
ЗАДАЧИ
Задача 1
За какую часть периода точка, совершающая гармонические колебания по закону косинуса, сместится на половину амплитуды, если в начальный момент она находилась в положении равновесия?
Решение
Колебания точки описываются уравнением (4)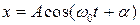 
. Поскольку при t = 0 смещение х = 0, то начальная фаза φ должна равняться π/2, т.е. уравнение имеет вид:
= 
.
По условию смещение 
, следовательно, 
(знак «минус» не учитываем, т.к. нас интересует первое попадание колеблющейся частицы в данное положение). Отсюда 
и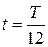 
.
|
|
|
Задача 2
Точка совершает колебания по закону 
(м), где 
2 с –1. Определить ускорение точки в момент времени, когда ее скорость равна 8 м/с.
Решение
Зависимости скорости и ускорения колеблющейся точки от времени задаются уравнениями (5) и (6). Из (5) 
и при 
Следовательно, 
. Тогда по (6) 
и с учетом того, что , получаем 
м/с2.
Задача 3
Максимальная скорость точки, совершающей гармонические колебания, равна 10 см/с, максимальное ускорение равно 100 см/с2. Найти циклическую частоту колебаний, их период и амплитуду.
Решение
Из сравнения формул (4), (5) и (6)
,
,
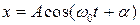видно, что 
.
Тогда 
. Откуда 
с–1. Период 
с. Амплитуда 
м.
Задача 4
Амплитуда гармонических колебаний материальной точки А = 0,02 м, полная энергия колебаний 
=3 · 10– 7 Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила F= 2,25 · 10–5 Н?
Решение
Из (10) W полн = W кин + W пот = 
можно выразить 
. Тогда, используя выражение (7), получим
.
Искомое смещение 
м.
Задача 5
В качестве физического маятника используется стержень, подвешенный за один из его концов. Чему равен период колебаний при длине стержня 1 м?
Решение
Для того, чтобы воспользоваться формулой (14) 
, необходимо по теореме Штейнера посчитать момент инерции стержня относительно оси, проходящей через точку подвеса:
.
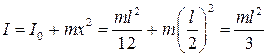Тогда, учитывая, что 
,
с.
Задача 6
Два одинаково направленных гармонических колебания заданы уравнениями 
и 
, где А1 = 1 см; А2 = 2 см; 
= 1 с–1. Определить амплитуду результирующего колебания А, его частоту 
и начальную фазу 
. Найти уравнение этого движения.
Решение
Преобразуем первое уравнение, заданное в условии задачи, к виду 
и получим
.
Тогда по формуле (16) 
амплитуда
результирующего колебания:
см2. 
м.
Частота результирующего колебания равна частоте складывающихся колебаний 
Гц.
Начальную фазу находим по формуле (17):
Начальная фаза 
рад.
Уравнение результирующего колебания имеет вид 
(м).
|
|
|
Задача 7
Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями 
(см) и 
(см). Найти уравнение траектории точки и построить ее, указав направление движения, если
(с –1).
Решение
Преобразуем второе уравнение к виду (4) 
и получим:
.
Как видно, разность фаз складывающихся колебаний 
и это соответствует частному случаю (21), когда уравнение траектории имеет вид: 
. Траекторией движения в этом случае является эллипс, приведенный к главным осям, уравнение которого 
Для того, чтобы указать направление движения точки, необходимо проследить, как меняется ее положение с течением времени. Для этого найдем координаты точки для двух ближайших моментов времени. Период результирующих колебаний 
с. Поэтому моменты времени, отличающиеся на одну секунду, можно считать достаточно близкими.
При 
: 
; 
= 0;
При 
с: 
; 
.
Следовательно, точка 1 имеет координаты (2; 0), а точка 2 – (1; 0,86). Это означает, что движение происходит против часовой стрелке.
Задача 8
Амплитуда колебаний математического маятника длиной 1 м за время 10 мин уменьшилась в 2 раза. Определить коэффициент затухания, логарифмический декремент затухания колебаний и количество колебаний, совершенных за это время. Записать уравнение колебаний, если в начальный момент маятник был отведен из положения равновесия на 5 см и отпущен.
Решение
Период и частоту колебаний математического маятника найдем из (13):
с, а 
(с–1).
Запишем отношение амплитуд (начальной 
см и через время t = 10 мин = 600 с):
,
следовательно, 
, отсюда 
с–1.
Количество колебаний N, совершенных за время t, найдем из того, что 
, а, значит, 
, и тогда
.
Логарифмический декремент затухания определим по (28):
.
Выбор гармонической функции для написания уравнения колебаний проведем на основании того, что в начальный момент смещение точки от положения равновесия равно амплитуде, а этому условию удовлетворяет функция косинус. Тогда уравнение данных затухающих колебаний имеет вид: 
(м).
Задача 9
Пружинный маятник, (жесткость пружины которого равна k = 10 Н/м, а масса груза m = 100 г) совершает вынужденные колебания в вязкой среде с коэффициентом сопротивления r = 0,02 кг/с. Определить коэффициент затухания β и резонансную амплитуду Арез, если амплитудное значение вынуждающей силы F0 = 10 мН.
Решение
Коэффициент затухания по (23):
с–1.
Собственная частота по (24):
с–1.
Тогда резонансная частота по (33):
м.
Задача 10
Поперечная волна распространяется вдоль упругого шнура со скоростью 15 м/с. Период колебаний точек шнура равен 1,2 с, амплитуда – 2 м. Определить фазу колебаний, смещение, скорость и ускорение точки, отстоящей не расстоянии 45 м от источника колебаний в момент времени t = 4 с. Начальная фаза равна нулю.
|
|
|
Решение
Длина волны по (35):
м.
Смещение точки определим из уравнения волны (36): 
м.
Фаза колебаний (аргумент косинуса) 
рад.
Для нахождения скорости точки продифференцируем 
по времени:
м/с
Дифференцирование скорости по времени позволяет найти ускорение:
м/с2.
Задача 11
Волна распространяется в упругой среде со скоростью v = 100 м/с. Наименьшее расстояние между точками среды, фазы которых противоположны, равно 1 м. Определить частоту колебаний.
Решение
По определению длиной волны называется наименьшее расстояние между точками, фазы которых одинаковы. Поэтому расстояние между точками, колеблющимися в противофазе, соответствует λ/2.
Отсюда длина волны λ = 2 м.
К этому же выводу можно прийти, используя формулу (40), определяющую связь между разностью фаз и разностью хода: 
, положив 
, а 
м.
Из формулы (35) частота:
Гц.
Задача 12
Мимо железнодорожной платформы проходит электропоезд. Наблюдатель, стоящий на платформе, слышит звук сирены поезда. Когда поезд приближается, кажущаяся частота звука 
= 1100 Гц; когда удаляется, кажущаяся частота 
= 900 Гц. Найти скорость поезда и частоту звука, издаваемого сиреной . Скорость звука 332 м/с.
Решение
В соответствии с формулой (45) для эффекта Доплера обозначим скорость наблюдателя vпр = 0, скорость поезда, подающего сигнал, vист, а скорость звука v = 332 м/с. Тогда
;
.
Отсюда
м/с;
Гц.
Задача 13
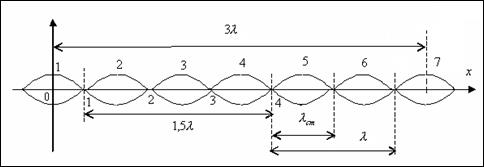
Определить длину бегущей волны, если в стоячей волне расстояние между:
1) первой и седьмой пучностями равно 15 см; 2) между первым и четвертым узлами равно 15 см.
 |
Решение
Координаты пучностей стоячей волны задаются формулой (47): 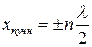. Тогда расстояние между первой и седьмой пучностями 
см. Отсюда 
см.
Координаты узлов стоячей волны задаются формулой (48) 
. Тогда расстояние между четвертым и первым узлом
см.
Отсюда 
см.
Задача 14
По цилиндрической трубе диаметром d = 20 см и длиной l = 5 м, заполненной сухим воздухом, распространяется звуковая волна со средней за период интенсивностью I = 50 мВт/м2. Найти среднюю энергию W звукового поля, заключенного в трубе. Скорость звука = 332 м/с.
Решение
По определению средняя плотность энергии (43) 
, а интенсивность (42) 
.
Тогда средняя энергия звукового поля
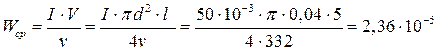Дж.
|
|
|
