 |
Расчет токов и напряжений в элементах цепи
|
|
|
|
Составление схемы исследуемой цепи
2.2 Расчет токов и напряжений в элементах цепи
2.3 Проверка результатов с помощью законов Кирхгофа
2. 4 Построение полной векторной диаграммы цепи
2.5 Расчет частотных характеристик цепи
Библиографический список
1. Задание к курсовой работе и указания по выполнению
1. Составить схему исследуемой цепи
Для этого на вход заданной цепи (вариант схемы цепи определяется преподавателем), как показано на рис. 1.1, подключить реальный источник гармонического напряжения с э.д.с. e(t) = Emcos (ωt), амплитуда, частота ω и внутреннее сопротивление Re которого также определяются в соответствии с вариантом.
 |
Рис. 1.1. Подключение источника напряжения к исследуемой цепи
Изобразить полученную схему цепи, проставить нумерацию элементов в соответствии с требованиями ГОСТ по оформлению чертежей и обозначить токи и напряжения на всех элементах, задав их положительные направления.
2. Рассчитать токи и напряжения в элементах цепи
Путем проведения аналитических расчетов необходимо определить амплитуды и начальные фазы токов и напряжений на всех элементах цепи при отсутствии нагрузки, в отчете привести описание расчетов, результаты представить в виде таблицы, аналогичной табл. 1.1.
Таблица 1.1 Результаты расчетов
| Элемент | Номинал | Um, мВ | Im, мА | ψU, град. | ψI, град. |
| Re | |||||
| R1 | |||||
| R2 | |||||
| R3 | |||||
| С1(L1) | |||||
| С2(L2) |
Так как в исследуемой цепи присутствуют реактивные элементы, то протекающие в цепи процессы могут быть описаны в комплексном виде. Поэтому при проведении аналитических расчетов необходимо использовать метод комплексных амплитуд.
|
|
|
В этом и последующих пунктах численные расчеты могут проводиться с применением вычислительной техники. В случае использования специальных программ (кроме «Калькулятора» ОС Windows) в отчете необходимо указать наименование использованной программы и описать подробный порядок действий с ней.
3. Проверить результаты расчетов
По результатам расчетов токов и напряжений провести проверку выполнения первого и второго законов Кирхгофа для узлов и контуров цепи.
4. Нарисовать полную векторную диаграмму цепи
Построить полную векторную диаграмму токов, напряжений и цепи источника. Все векторы, изображенные на рисунке должны быть подписаны. Допускается векторы, относящиеся к токам и напряжениям, изображать разными цветами или изобразить на двух разных диаграммах.
5. Рассчитать частотные характеристики цепи
Для выполнения расчета необходимо:
– определить комплексный коэффициент передачи по напряжению исследуемой цепи
, (1.1)
где 
и 
- комплексные амплитуды выходного и входного напряжений;
– рассчитать амплитудно-частотную (АЧХ) и фазочастотную (ФЧХ) характеристики;
– построить графики АЧХ и ФЧХ.
2. курсовая работа
Рассмотрим пример выполнения задания курсовой работы для схемы, приведенной на рис. 3.1 со следующими исходными данными: Em = 10 В, Re = 104 Ом, R1 = R2 = R3 = R = 2·103 Ом, C1 = C2 =1 нФ, ω = 105 рад/с.
Рис. 2.1 Схема исследуемой цепи
Составление схемы исследуемой цепи
В соответствии с п. 1 задания к курсовой работе ко входу схемы необходимо подключить источник э.д.с. с внутренним сопротивлением (т.е. дорисовать слева к имеющейся схеме условно-графическое обозначение источника э.д.с. и сопротивления), произвести нумерацию элементов (слева направо, сверху вниз) и расставить токи. Выбор направлений протекания токов во всех ветвях определяется в зависимости от направления э.д.с. После указанных действий исходная схема преобразуется к виду, приведенному на рис. 2.2.
|
|
|
Рис. 2.2. Преобразованная схема исследуемой цепи
Расчет токов и напряжений в элементах цепи
Расчет в данной схеме целесообразно начать с простого соединения двух элементов R3 и C2. Комплексное сопротивление этого участка цепи как любого параллельного соединения (см. формулу (2.19)) равно
, (3.1)
где комплексное сопротивление 
активного сопротивления R3 равно самому этому сопротивлению (
Ом), а комплексное сопротивление 
емкости С2 равно
Ом. (3.2)
Поэтому, подставляя эти значения в (3.1), получаем, что комплексное сопротивление параллельного участка цепи R3 C2 равно
Ом. (3.3)
В дальнейшем, при нахождении токов и напряжений элементов цепи, необходимо будет применять закон Ома в комплексной форме, а следовательно, придется делить и умножать комплексные величины. Это удобнее делать если числа будут представлены в показательной форме. Для перевода числа в показательную форму необходимо найти его модуль и аргумент. Модуль полученного в (3.3) комплексного числа равен
Ом, (3.4)
А аргумент
. (3.5)
Поэтому комплексное сопротивление участка R3C2 можно записать, как 
Ом.
Участок цепи R2R3C2 представляет собой последовательное соединение сопротивления R2 параллельного соединения элементов R3C2. Поэтому комплексное сопротивление всего участка R2R3C2 равно
. (3.6)
Комплексное сопротивление 
активного сопротивления R2 равно самому этому сопротивлению (
Ом). Следовательно, комплексное сопротивление рассматриваемого участка в соответствии с (3.3) и (3.6) можно определить по формуле
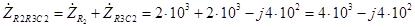Ом. (3.7)
|
|
|
Точно также, как и в предыдущем случае, полученный результат целесообразно сразу преобразовать в экспоненциальную форму. Для этого необходимо найти модуль и аргумент. Модуль полученного в (3.7) комплексного числа равен
Ом, (3.8)
А аргумент
. (3.9)
Поэтому комплексное сопротивление участка цепи можно записать, как 
Ом. Сопротивление R1 подключено к участку цепи R2R3C2 параллельно. Следовательно, комплексное сопротивление этого участка цепи как любого параллельного соединения равно
, (3.10)
Комплексное сопротивление 
активного сопротивления R1 равно самому этому сопротивлению (
Ом).
Следовательно, комплексное сопротивление рассматриваемого участка R1R2R3C2 можно рассчитать по формуле
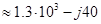Ом. (3.11)
|
|
|
