29. Динамические характеристики средств измерений.

29. Динамические характеристики средств измерений.

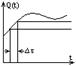
Измерение Q(t) называется динамическим, если изменением измеряемой величины во времени пренебречь нельзя. Это, напр., измерение мгновенного значения переменного U-я и I. Измерение амплитуды, частоты, фазы того же переменного U-я или I к динамическим не относятся. При воздействии на СИ изменяющейся во времени физической величины начинают проявляться инерционный свойства СИ. Оно не успевает реагировать на изменение входного сигнала Q(t), в результате чего выходной сигнал оказывается искаженным по сравнению с входным.

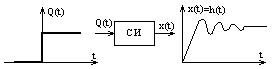
Если выходной сигнал x(t) пересчитать на вход с помощью обратной функции преобразования сигнала, то результат будет отличаться от входного воздействия на какую-то величину ζ (t) – дзетта=Q(t)-x(t). Для определения ζ (t) нужно знать инерционные или динамические свойства СИ. Эти свойства выражаются с помощью динамических характеристик, которые однозначно устанавливают отклик СИ на входное воздействие.

 

31. Суммирование откликов (операция свертки). Интегралы свертки.

Отклик СИ на единичный импульс во временном представлении наз. импульсной хар-кой и обозн-ся как g(t). Поскольку единичный импульс является производной от единичной ступени, то отклик на единичный импульс на выходе линейного СИ (амплитудная хар-ка) является производной отклика на единичную ступень (переходная хар-ка): g(t)=h’(t). Используя это соотношение из интеграла Д м. записать:

Эти выражения при выборе соответствующих моделей входных воздействий позволят с помощью импульсной хар-ки установить пределы, в которых находится ζ (t).

Переходная или импульсная хар-ки определяются экспериментально. При их использовании по м-ду суперпозиции осуществляется вначале разложение входной функции на элементарные функции времени, а затем суммируются отклики на них. Эту последнюю операцию называют свертыванием, а сами интегралы – интегралами свертки. Из них выбирается тот интеграл, у которого проще подынтегральная функция.

30. Отклики средств измерений на входные воздействия (единичная ступень, единичный импульс). Метод суперпозиции.

1. Простейшим видом такого воздействия является единичная ступень: Q(t)=0 при t≤ 0; и Q(t)=1 при t> 0. Отклик на нее обозначается через h(t) и называется переходной характеристикой. h(t) отражает переходный процесс от одного установившегося состояния на выходе СИ к другому при переходе входного воздействия от 0 к 1. Единичная ступень еще обозначается 1(t). Зная переходную характеристику СИ, м. рассчитать его реакцию или отклик на любое входное воздействие. Расчет основывается на принципе суперпозиции: каждое входное воздействие м. представить как сумму Q(0)·1(t) и мн-во следующих через =ые промежутки времени Δ τ ступеней.

Отклик на каждую ступень, смещенную на время n·Δ τ пропорционален величине этой ступени, т. е. Δ Q(n·Δ τ )≈ Δ τ Q’(n·Δ τ ).

Переходя к пределу при n→ ∞ b Δ τ → 0, получим одну из форм интеграла Дюамеля (интеграла наложения):

Можно было бы предположить, что с помощью этих формул при известной переходной характеристике h(t) решается основная задача измерения – определение входного воздействия Q(t) по отклику на него x(t). Однако, вследствие того, что x(t) и h(t) при измерениях всегда известны с некоторой неопределенностью, решение этой задачи наталкивается на исключительные трудности.

На практике чаще всего ограничиваются оценкой ζ (t) сверху и снизу. Для этого, учитывая априоную информацию об изменяемой физ. вел. Q(t), выбирают модели входных воздействии Q₁(t) и Q₂(t), при которых ζ ₁(t) и ζ ₂(t) будут соответственно больше заданной ζ (t). Затем с помощью одного из интегралов Д при известной переходной характеристике, вычисляют x₁(t) и x₂(t), после чего по известной формуле ζ (t)= Q(t)-x(t) определяют ζ ₁(t) и ζ ₂(t), позволяющие установить границы интервала неопределенности измерений Q(t).

2. Другим видом испытательного сигнала простейшего входного сигнала является единичный импульс: Q(t)=0 при t≠ 0, и Q(t)=∞ при t=0. Он называется так потому, что площадь, ограниченная этой фигурой, равна 1-ой производной от единичной ступени – δ (t) и называется дельта-функцией или функцией Дирака.

Отклик СИ на единичный импульс м. рассматривать во временном, частотном или операторном представлении. В зависимости от этого различают 3 вида динамических характеристик: 1) импульсную хар-ку; 2) комплексный коэффициент преобразования (компл. коэф. передачи); 3) передаточную функцию.

Отклик СИ на единичный импульс во временном представлении наз. импульсной хар-кой и обозн-ся как g(t). Поскольку единичный импульс является производной от единичной ступени, то отклик на единичный импульс на выходе линейного СИ (амплитудная хар-ка) является производной отклика на единичную ступень (переходная хар-ка): g(t)=h’(t). Используя это соотношение из интеграла Д м. записать:

Эти выражения при выборе соответствующих моделей входных воздействий позволят с помощью импульсной хар-ки установить пределы, в которых находится ζ (t).

Переходная или импульсная хар-ки определяются экспериментально. При их использовании по м-ду суперпозиции осуществляется вначале разложение входной функции на элементарные функции времени, а затем суммируются отклики на них. Эту последнюю операцию называют свертыванием, а сами интегралы – интегралами свертки. Из них выбирается тот интеграл, у которого проще подынтегральная функция.

Спектр отклика СИ на единичный импульс называется комплексным коэффициентом преобразования и обозначается , где модуль к(ω ) и аргумент φ (ω ) называются соответственно АЧХ и ФЧХ.

3. При подаче на вход СИ гармонического колебания Q(t)=Q_maxsin(ω t+φ _Q), амплитуда x_m отклика x(t): x(t)=x_msin(ω t+φ _x) на выходе линейного СИ связана с амплитудой входного воздействия через коэффициент передачи к на частоте ω : x_m=кQ_m, а разность фаз φ =φ _x-φ _y определяет задержку выходного сигнала по отношению к входному на той же частоте.

 

Подавая на вход сигналы различных частот м. построить АЧХ и ФЧХ.

Изображение по Лапласу отклика СИ на единичный импульс называется передаточной функцией и обозначается как W(p). Т. о. передаточная функция связана с импульсной хар-кой прямым преобразованием Лапласа. Важной особенностью передаточной функции является возможность ее определения теоретическим путем посредством решения операторным м-дом ДУ-я, описывающего работу СИ.

Однозначная связь между рассмотренными динамическими хар-ми означает их полную эквивалентность и предполагает возможность реального выбора в каждом конкретном случае наиболее подходящей из них. Так, если работа СИ описывается известным ДУ-ем, то в кач. динамической хар-ки целесообразно выбрать передаточную функцию, получаемую путем решения этого ур-ния операторным м-дом. Если динамическая хар-ка определяется экспериментально, то ее выбор зависит от типов имеющихся приборов и видов входных воздействий. Вполне возможен как временной так и частотный подход к решению вопроса.

Динамические хар-ки относятся к нормируемым метрологическим хар-кам СИ и вследствие этого должны поверяться.

 

 

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: