 |
19. Оценки числовых характеристик законов распределения (точечная, интервальная, состоятельная, несмещенная, эффективная).
|
|
|
|
19. Оценки числовых характеристик законов распределения (точечная, интервальная, состоятельная, несмещенная, эффективная).
Неопределенность результата измерения из-за случайного характера отсчета может быть уменьшена при многократном измерении одной и той же величины. Многократные измерения организуют путем проведения однократных измерений одновременном несколькими экспертами или средствами измерений, либо повторяя однократное измерение несколько раз (если измеряемая величина не меняется во времени). Если при этом можно было бы определить среднее значение измеряемой величины 
, то неопределенность результата измерения, выраженная случайностью отсчета была полностью исключена, т. к. 
- величина неслучайная.
На практике этого добиться нельзя из-за конечного числа отсчетов, можно лишь как-то определить 
, определить это значение с некоторой неопределенностью.
Оценки числовых характеристик з-нов распределения вероятности случайной величины, изображенные точкой на числовой характеристике, называются точечными, интервалами – интервальными. В отличие от числовых характеристик, оценки являются случайными величинами, причем их значения зависят от числа измерений n, а распределение вероятности - от з-на распределения вероятности.
Теория вероятности говорит, что оценки должны удовлетворять 3-ем требованиям:
1. они д. б. несмещенными
2. состоятельными
3. эффективными
Состоятельной называется оценка, которая сходится по вероятности к оцениваемой величине.
Несмещенной является оценка, математическое ожидание которой равно оцениваемой величине.
Эффективной называют ту из нескольких возможных несмещенных оценок, которая имеет наименьшую дисперсию.
|
|
|
Перечисленным требованиям удовлетворяет такая точечная оценка, как среднее арифметическое:
20. Оценка дисперсии и стандартное отклонение результата многократного измерения.
Если результаты однократных измерений вносится одна и та же поправка, то действительное значение измеряемой величины при многократном измерении выражается той же формулой: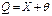 
, а показания прибора 
Если же однократные измерения имеют разные поправки (измеряются разными приборами):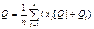 
.
В том и другом случае результат многократного измерения остается случайной величиной.
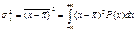
Дисперсия среднего арифметического в n раз меньше дисперсии отсчета. Отсюда следует важнейшее свойство результата многократного измерения: его неопределенность меньше, чем неопределенность результата однократного измерения.
В дальнейшем индексы при показателях качества результатов многократного измерения могут быть опущены: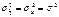 
. Т. о. для выражения неопределенности результата многократного измерения надо найти дисперсию или среднеквадратическое отклонение отсчета. Т. к. число отсчетов конечно, то реально может быть вычислены только соответствующие оценки. В качестве точечной оценки 
естественно было бы выбрать среднее арифметическое квадратов отклонения отсчетов от 
. Однако, эта оценка немного смещена. Несмещенной является следующая оценка дисперсий:
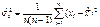и соответственно оценка среднеквадратического отклонения 
:
, которая носит название стандартного отклонения(СТО) и обозначается буквой S.
Оценка дисперсий и стандартное отклонение результатов многократного измерения соответственно определяется как:
При записи результата высокоточного многократного измерения перечисляются все причины его неопределенности с указанием способа учета каждого из них. Кроме того, т. к. S зависит от числа отсчетов, указывается число n- число отсчетов.
|
|
|
Для многократного измерения указывается:
|
|
|
