 |
Метод наименьших квадратов
|
|
|
|
Кафедра «Эксплуатация транспортных и технологических машин»
Парный линейный
Регрессионный
И корреляционный
Анализ
Экспериментальных данных
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ТЕСТЫ
к выполнению контрольной работы
и практических работ по дисциплинам
«Основы научных исследований (ОНИ)»
для студентов направления 23.03.03 «Эксплуатация
транспортно-технологических машин и комплексов»,
21.03.01 «Нефтегазовое дело»
всех форм обучения
Сургут 2017 г.
Утверждено учебно-методической комиссией
Федерального государственного бюджетного образовательного
учреждения высшего образования
филиала в г. Сургуте
Тюменского индустриального университета
Составил: доцент, канд. техн. наук Некрасов В.И.
Оформление: уч. мастер Песчанская М.А.
филиал в г. Сургуте
Тюменский индустриальный университет, 2017 г.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ………………………………………………………………3
1. Начальные сведения……………………………………………………..4
2. Варианты заданий………………………………………………………..9
3. Парный линейный регрессионный и корреляционный анализ
экспериментальных данных……………………………………………11
3.1. Основные определения……………………………………………..11
3.2. Метод группировок…………………………………………………13
3.3. Метод средних………………………………………………………18
3.4. Метод наименьших квадратов……………………………………..21
3.4.1. Прямая регрессия…………………………………………………22
3.4.2. Обратная регрессия……………………………………………….26
3.4.3. Корреляция………………………………………………………...27
3.4.4. Ортогональная регрессия………………………………………...28
Содержание, объем и основные правила оформления
|
|
|
расчетно-пояснительной записки……………………………………….
4. Тесты…………………………………………………………………….31
ПРИЛОЖЕНИЕ……………………………………………………………32
ИСТОЧНИКИ……………………………………………………………...34
ВВЕДЕНИЕ
Современное производство требует от специалиста умения самостоятельно ставить и решать различные принципиально новые вопросы, чего нельзя сделать без овладения им основами научных исследований (ОНИ). Научная подготовка студентов в вузах – одна из важнейших сторон их обучения.
Современный специалист должен: владеть методикой НИ (научных исследований), их планированием и организацией, уметь отбирать и анализировать необходимую информацию, формулировать цель и задачи НИ, обосновывать теоретическую базу, планировать и проводить эксперименты, обрабатывать результаты измерений, оценивать погрешность наблюдений, сопоставлять результаты эксперимента с теоретическими предпосылками, формулировать выводы НИ, составлять отчет, доклад или статью по результатам НИ.
Цель контрольной работы – закрепить знания в области методов обработки экспериментальных данных, приобрести навыки расчетов коэффициентов регрессии и корреляции, оценивать статистическую значимость этих коэффициентов, получать уравнения прямой и обратной регрессии, оценивать адекватность этих уравнений, интерполировать и экстраполировать, интерпретировать полученные результаты и т.д.
НАЧАЛЬНЫЕ СВЕДЕНИЯ
Учебная дисциплина «Основы научных исследований» основана на курсе «Высшая математика» и создает основу для изучения специальных дисциплин.
Некоторые студенты, в первую очередь, заочной формы обучения не имеют знаний на уровне элементарной математики. В последние годы многие из них не воспринимают даже такое понятие, как «катет», необходимое для выполнения работы.
|
|
|
Начнем с простейшего.
Рассмотрим прямоугольник АВС (рис. 1.). Он имеет два катета: противо лежащий ВС и при лежащий АВ, а также гипотенузу А С.
При выполнении работы надо определить угловой коэффициент регрессии, равный тангенсу угла САВ. Тангенс угла САВ равен отношению противо лежащего катета ВС к при лежащему катету АВ.
b 1(yх) = tg α = ВС/ АВ.
Исходные данные для контрольной работы выбирают из таблицы 1. В верхней строке приведены координаты точек по оси абсцисс (Х) от -6 до 13. В следующих строках – координаты точек по оси ординат (У). Для статистической обработки надо выбрать 10 точек.
Например, для 1-го варианта: Х 1 = -5, У 1 = 1; Х 2 = -3, У 2 =2; Х 3 = -1, У 3 = 4; Х 4 = 1, У 4 = 3; Х 5 = 3, У 5 = 5; Х 6 = 5, У 6 = 4; Х 7 = 7, У 7 = 6; Х 8 = 9, У 8 = 5; Х 9 = 11, У 9 = 7; Х 10 = 13, У 10 = 7.
ВАРИАНТЫ ЗАДАНИЙ
Таблица 1
Исходные данные
| № варианта | Верхняя строка – ось абсцисс – х, далее строки – ось ординат - у | |||||||||||||||||||
| -6 | -5 | -4 | -3 | -2 | -1 | |||||||||||||||
| -3 | -3 | -5 | ||||||||||||||||||
| -4 | -4 | -6 | ||||||||||||||||||
| -12 | -10 | -7 | -8 | -5 | -1 | |||||||||||||||
| -12 | -10 | -7 | -8 | -5 | -1 | |||||||||||||||
| -1 | -2 | -3 | -2 | -4 | -5 | |||||||||||||||
| -1 | -2 | -1 | -3 | -4 | ||||||||||||||||
| -1 | -4 | -6 | ||||||||||||||||||
| -2 | -5 | -7 | ||||||||||||||||||
| -1 | -2 | -4 | -4 | -6 | -7 | |||||||||||||||
| -6 | -5 | -5 | -4 | -3 | -3 | -2 | -1 | |||||||||||||
| -6 | -5 | -4 | -4 | -3 | -2 | -2 | -1 | |||||||||||||
| -6 | -6 | -5 | -5 | -5 | -4 | -4 | -4 | -3 | -3 | |||||||||||
| -3 | -2 | -2 | -2 | -1 | -1 | |||||||||||||||
| -14 | -12 | -11 | -10 | -9 | -8 | -6 | -5 | -4 | -3 | |||||||||||
| -13 | -12 | -11 | -9 | -8 | -7 | -6 | -4 | -3 | -2 | |||||||||||
| -14 | -13 | -12 | -12 | -11 | -11 | -10 | -9 | -9 | -8 | |||||||||||
| -8 | -7 | -6 | -6 | -5 | -4 | -4 | -3 | -3 | -2 |
|
|
|
|
|
|
Номер варианта контрольной работы определяется по номеру студента в списке группы. Возможно изменение темы контрольной работы по согласованию с преподавателем данной дисциплины.
ПАРНЫЙ ЛИНЕЙНЫЙ
РЕГРЕССИОННЫЙ И КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
Основные определения
Подавляющее большинство формул, используемых в технических дисциплинах, относятся к так называемым "парным" зависимостям типа  .
.
Задача обработки данных заключается в аналитическом представлении искомой функциональной зависимости, т. е. в подборе формулы, описывающей результаты эксперимента. Особенность задачи состоит в том, что наличие случайных ошибок измерения (или как говорят наличия “шума“ в эксперименте), при описании результатов, не должно включать все опытные значения. Другими словами, график искомой функции не должен проходить через все точки (соединять их), а должен по возможности сглаживать “шум" – плавная линия (в нашем случае прямая) должна проходить в области расположения точек.
Регрессионный анализ дает возможность получить математическую модель объекта исследования - уравнение, аналитическое представление функциональной зависимости одной величины y от другой величины x.
Линейный регрессионный анализ, при помощи метода наименьших квадратов (МНК), состоит в том, что, зная положение экспериментальных точек на плоскости, нужно так провести линию регрессии, чтобы сумма квадратов отклонений вдоль выбранной оси координат от этих точек до проведенной линии регрессии была бы минимальной.
Для проведения регрессионного анализа по МНК предъявляется следующее требование: уравнение должно быть линейным по параметрам или допускать возможность линеаризации - спрямления. В этом случае получим уравнение прямой регрессии в декартовых координатах
У = b0(yх) + b1(yх) Х.
Также иногда применяют обратную регрессию
Х = b0(xy) + b1(xy) У
где: b 0 (yх) - свободный член уравнения регрессии; геометрически он представляет собой расстояние от начала координат до точки пересечения линии прямой регрессии с ординатой (это отрезок, отсекаемый на ординате линией регрессии); (yх) – У относительно Х или У от Х.
Для обратной регрессии b 0 (xy) - это отрезок на абсциссе, отсекаемый этой прямой; (xy) - Х относительно У или Х от У.
b 1(yх) – угловой коэффициент уравнения прямой регрессии - тангенс угла наклона линии прямой регрессии к оси абсцисс,
|
|
|
b 1(xy) - угловой коэффициент уравнения обратной регрессии - тангенс угла наклона линии обратной регрессии к оси ординат.
Корреляционный анализ изучает усредненный закон поведения каждой из величин в зависимости от значений другой величины, а также меру зависимости (тесноту взаимосвязи) между рассматриваемыми величинами.
Корреляция между величинами x и y называется линейной, если обе функции регрессии (y от x и x от y) линейны. Угловые коэффициенты этих прямых выражаются через коэффициент корреляции, который также служит мерой линейной зависимости между величинами.
Мера зависимости между величинами характеризуется коэффициентом корреляции 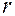 (для прямых) или корреляционным отношением
(для прямых) или корреляционным отношением 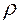 (для нелинейных зависимостей - кривых).
(для нелинейных зависимостей - кривых).
Коэффициент корреляции представляет собой безразмерную величину, значение и знак которой характеризуют направление и величину подобной взаимосвязи между y и x.
Значения коэффициента корреляции могут изменяться от -1 до +1, включая 0. Коэффициент корреляции, равный +1 или -1, указывает на наличие строгой функциональной (детерминированной, ортогональной) взаимосвязи. 0 - говорит об отсутствии какой бы то не было взаимосвязи. Коэффициент корреляции, отличный от 1, указывает на случайную (стохастическую) взаимосвязь.
Знак коэффициента указывает на направление взаимосвязи между двумя переменными. Этот знак (+ или -) соответствует знаку углового коэффициента b 1(yх).
Абсолютное значение коэффициента (без учета знака) характеризует силу или тесноту взаимосвязи.
Уравнение прямой линии может быть получено различными способами: методом Асковица, методом группировки, методом средних, методом наименьших квадратов (МНК) и т.д.
Выполним обработку условных экспериментальных данных несколькими методами, начиная с простейшего.
Метод группировок
Этот метод является наиболее простым. Для применения этого метода необходимо знать хотя бы одну точку прямой, так как определяется только угловой коэффициент. Построение прямой производится очень быстро.
Если задан ряд экспериментальных точек с координатами Х и Y, то угловой коэффициент прямой, принадлежащей этим точкам, можно вычислить по формуле
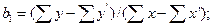
где Х и Y – координаты m точек, сгруппированных в одной части графика, а Х’ и Y’ – координаты m точек, сгруппированных в другой части графика.
Если интервалы между значениями Х примерно одинаковы, то имеющиеся данные необходимо разделить на три примерно равные группы и использовать группу точек с координатами Х и Y, находящихся в верхней части графика, и группу точек с координатами Х’ и Y’, находящихся в нижней части графика, исключив среднюю группу точек. В этом случае нарушается общее практическое правило статистического анализа: «Статистический критерий оказывается наиболее эффективным при использовании всех данных».
Например, имеем 8 пар измерений, n = 8:
Y: 9,0; 11,0; 9,0; 9,5; 6,5; 7,0; 4,5; 5,0.
Х: 12,5; 11,0; 10,0; 8,5; 7,0; 5,0; 4,0; 1,5.
Эти исходные данные и результаты статистической обработки сводим в таблицу 2. В таблице 2 приведены результаты статистической обработки этих данных и другими методами.
Для контрольной работы надо приготовить таблицу для 10 точек.
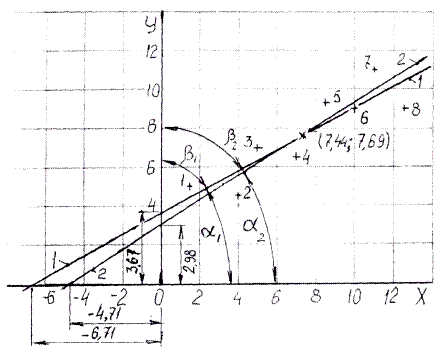
Наносим точки на график – рис.1. Делим массив данных на три примерно равные группы: выделяем по три точки в верхней и нижней части графика (первые три и последние три пары значений), две точки в средней части не используем.

Рис. 1. Линии регрессии по методу группировок (1)
и методу средних (2)
1. Определяем угловой коэффициент уравнения прямой регрессии
b 1(yх) = 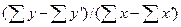 =
=
=[(9,0+11,0+9,0)–(7,0+4,5+5,0)]/[(12,5+11,0+10,0)–(5,0+4,0+1,5)] = (29,0-16,5)/(33,5-10,5) = 12,5/23 = 0,543.
Прямая должна проходить по опорной точке, расположенной в центре массива данных и имеющей координаты: Х ср = 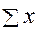 /n = 59,5/8 = 7,44 и Y ср =
/n = 59,5/8 = 7,44 и Y ср =  /n = 61,5/8 = 7,69.
/n = 61,5/8 = 7,69.
В уравнение прямой У = b 0(yх) + b 1(yх) Х подставляем рассчитанные значения Х ср и Y ср, получим 7,69 = b 0(yх) + 0,54х 7,44.
2. Определяем свободный член уравнения прямой регрессии
b 0(yх) = Y ср - b 1(yх) Х ср = 7,69 - 0,54х 7,44 = 3,67.
Получили искомое уравнение прямой регрессии
У р = b 0(yх) + b 1(yх) Х = 3,67 + 0,54 Х.
3. Определяем расчетные значения Y P, абсолютные отклонения экспериментальных значений от расчетных Δ Y, а также квадраты этих отклонений Δ Y ² и сводим их в таблицу 2:
У 1 р= 3,67 + 0,54 Х 1 = 3,67 + 0,54 х 1,5 = 4,48.
 Y 1 = У 1 эк - У 1 р = 5,0 – 4,48 = 0,52;
Y 1 = У 1 эк - У 1 р = 5,0 – 4,48 = 0,52; 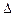 Y ²1 = 0,2704.
Y ²1 = 0,2704.
У 2 р= 3,67 + 0,54 Х 2 = 3,65 + 0,54 х 4,0 = 5,83.
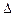 Y 2 = 4,5 – 5,83 = - 1,33;
Y 2 = 4,5 – 5,83 = - 1,33; 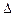 Y ²2 = 1,7689 и т.д.
Y ²2 = 1,7689 и т.д.
При методе группировок линия прямой регрессии совпадает с линией обратной регрессии. Уравнение обратной регрессии для той же линии
Х р = b 0(xy) + b 1(xy) У
4. Определяем угловой коэффициент уравнения обратной регрессии
b 1(ху) = 23,0/12,5 = 1,84 или b 1(ху) = 1,0/ b 1(ух) =1,0/0,543= 1,84.
5. Определяем свободный член уравнения прямой регрессии
b 0 (ху) = Х ср - b 1 (ху) У ср = 7,44 – 1,84 х 7,69 = - 6,71.
6. Определяем расчетные значения Хр, абсолютные отклонения экспериментальных значений от расчетных ΔX, а также квадраты этих отклонений ΔX² и сводим их в таблицу 2:
Хр = b 0 (ху) + b 1 (ху) У = - 6,71 + 1,84 У.
Х 1р = b 0 (ху) + b 1 (ху) У 1 = - 6,71 + 1,84 х 5,0 = 2,49.
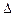 X 1 = 1,5 – 2,49 = - 0,99;
X 1 = 1,5 – 2,49 = - 0,99; 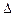 X 12 = 0,9801.
X 12 = 0,9801.
Х 2р = b 0 (ху) + b 1 (ху) У 2 = - 6,71 + 1,84 х 4,5 = 1,57.
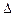 X 2 = 4,0 – 1,57 = 2,43;
X 2 = 4,0 – 1,57 = 2,43; 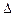 X 22 = 5,9049 и т.д.
X 22 = 5,9049 и т.д.
7. Наносим линию на рис.1 и обозначаем коэффициенты уравнений регрессии.
Таблица 2
Исходные данные и результаты статистической обработки
этих данных различными методами
| ИСХОДНЫЕ ДАННЫЕ | ||||||||||||||||||
| n | 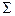
| |||||||||||||||||
| x | 1,5 | 4,0 | 5,0 | 7,0 | 8,5 | 10,0 | 11,0 | 12,5 | 59,5 | |||||||||
| y | 5,0 | 4,5 | 7,0 | 6,5 | 9,5 | 9,0 | 11,0 | 9,0 | 61,5 | |||||||||
МЕТОД ГРУППИРОВОК: 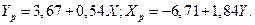
| ||||||||||||||||||
| yp | 4,48 | 5,83 | 6,37 | 7,45 | 8,26 | 9,07 | 9,61 | 10,42 | ||||||||||
| Δy | 0,52 | -1,33 | 0,63 | -0,95 | 1,24 | -0,07 | 1,39 | -1,42 | ~0,0 | |||||||||
| Δy² | 0,2704 | 1,7689 | 0,3969 | 0,9025 | 1,5376 | 0,0049 | 1,9321 | 2,0164 | 8,83 | |||||||||
| xp | 2,49 | 1,57 | 6,17 | 5,25 | 10,77 | 9,85 | 13,53 | 9,85 | ||||||||||
| Δx | -0,99 | 2,43 | -1,17 | 1,75 | -2,27 | 0,15 | -2,53 | 2,65 | ~0,0 | |||||||||
| Δx² | 0,9801 | 5,9049 | 1,3689 | 3,0625 | 5,1529 | 0,0225 | 6,4009 | 7,0225 | 29,92 | |||||||||
МЕТОД СРЕДНИХ: 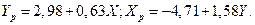
| ||||||||||||||||||
| yp | 3,93 | 5,5 | 6,13 | 7,39 | 8,34 | 9,28 | 9,91 | 10,86 | ||||||||||
| Δy | 1,07 | -1,0 | 0,87 | -0,89 | 1,16 | -0,28 | 1,09 | -1,86 | ~0,0 | |||||||||
| Δy² | 1,1449 | 1,00 | 0,7569 | 0,7921 | 1,3456 | 0,0784 | 1,1881 | 3,4596 | 9,7656 | |||||||||
| xp | 3,19 | 2,4 | 6,35 | 5,56 | 10,3 | 9,51 | 12,67 | 9,51 | ||||||||||
| Δx | -1,69 | 1,6 | -1,35 | 1,44 | -1,8 | 0,49 | -1,67 | 2,99 | ≈0,0 | |||||||||
| Δx² | 2,8561 | 2,56 | 1,8225 | 2,0736 | 3,24 | 0,2401 | 2,7889 | 8,9401 | 24,52 | |||||||||
МНК: 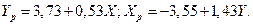
| ||||||||||||||||||
| x² | 2,25 | 16,0 | 25,0 | 49,0 | 72,25 | 100,0 | 121,0 | 156,25 | 541,75 | |||||||||
| y² | 25,0 | 20,25 | 49,0 | 42,25 | 90,25 | 81,0 | 121,0 | 81,0 | 509,75 | |||||||||
| xy | 7,5 | 18,0 | 35,0 | 45,5 | 80,75 | 90,0 | 121,0 | 112,5 | 510,25 | |||||||||
| (x+y) | 6,5 | 8,5 | 12,0 | 13,5 | 18,0 | 19,0 | 22,0 | 21,5 | 121,0 | |||||||||
| (x+y) ² | 42,25 | 72,25 | 144,0 | 182,25 | 324,0 | 361,0 | 484,0 | 462,25 | 2072,0 | |||||||||
| yp | 4,53 | 5,85 | 6,38 | 7,44 | 8,24 | 9,03 | 9,56 | 10,35 | ||||||||||
| Δy | 0,47 | -1,35 | 0,62 | -0,94 | 1,26 | -0,03 | 1,44 | -1,35 | ~0,0 | |||||||||
| Δy² | 0,2209 | 1,8225 | 0,3844 | 0,8836 | 1,5876 | 0,0009 | 2,0736 | 1,8225 | 8,80 | |||||||||
| xp | 3,6 | 2,855 | 6,46 | 5,745 | 10,035 | 9,32 | 12,18 | 9,32 | ||||||||||
| Δx | -2,1 | 1,115 | -1,46 | 1,255 | -1,535 | 0,68 | -1,18 | 3,18 | ~0,0 | |||||||||
| Δx² | 4,41 | 1,2432 | 2,1316 | 1,5750 | 2,3562 | 0,4624 | 1,3924 | 10,1124 | 23,68 | |||||||||
ОРТОГОНАЛЬНАЯ РЕГРЕССИЯ: 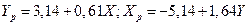
| ||||||||||||||||||
| yp | 4,055 | 5,58 | 6,19 | 7,41 | 8,325 | 9,24 | 9,85 | 10,765 | ||||||||||
| Δy | 0,945 | -1,08 | 0,81 | -0,91 | 1,175 | -0,24 | 1,15 | -1,765 | ~0,0 | |||||||||
| Δy² | 0,8930 | 1,1664 | 0,6561 | 0,8281 | 1,3806 | 0,0576 | 1,3225 | 3,1152 | 9,42 | |||||||||
| xp | 3,06 | 2,24 | 6,34 | 5,52 | 10,44 | 9,62 | 12,9 | 9,62 | ||||||||||
| Δx | -1,56 | 1,76 | -1,34 | 1,48 | -1,94 | 0,38 | -1,9 | 2,88 | ~0,0 | |||||||||
| Δx² | 2,4336 | 3,0976 | 1,7956 | 2,1904 | 3,7636 | 0,1444 | 3,61 | 8,2944 | 25,33 | |||||||||
| Δh | 0,808 | -0,92 | 0,693 | -0,775 | 1,005 | -0,203 | 0,984 | -1,505 | ~0 | |||||||||
| Δh² | 0,653 | 0,847 | 0,4805 | 0,600 | 1,010 | 0,0412 | 0,968 | 2,2647 | 6,86 | |||||||||
Поскольку данный метод не является точным, то нецелесообразно полностью полагаться только на него.
Метод средних
Этот метод применяется для построения эмпирических зависимостей парного простейшего вида. Метод состоит в том, что параметры эмпирической формулы определяются из условия равенства нулю суммы всех отклонений наблюдаемой величины от среднего значения.
Вначале результаты наблюдений выравниваются (спрямляются, в контрольной работе данные уже линеаризированы), а затем для полученных новых переменных Х и У, связанных линейной зависимостью У р = b 0(yх) + b 1(yх) Х, находят коэффициенты b 0(yх) и b 1(yх).
Для этого подставляют в уравнение полученные значения Х и У попарно, полученные равенства (условные уравнения) разбивают на две примерно равные группы. Группировка условных уравнений возможна несколькими способами, лучшим будет тот, который приводит к решению, дающему наименьшую сумму квадратов отклонений. Обычно уравнения группируют в последовательности опытных данных, разбивая их на равные или приблизительно равные части. Вообще равенства разбивают на столько групп, сколько коэффициентов уравнения предстоит определить.
Каждую группу уравнений почленно складывают. Получают систему из двух уравнений, из которых и находят коэффициенты, а затем переходят к натуральным переменным.
Например, имеем 8 пар измерений из предыдущего примера (см. табл.2).
Х: 1,5; 4,0; 5,0; 7,0; 8,5; 10,0; 11,0; 12,5.
Y:5,0; 4,5; 7,0; 6,5; 9,5; 9,0; 11,0; 9,0.
1. Составляем систему уравнений из двух групп для уравненияпрямой регрессия Y = b 0 (ух)+ b 1 (ух) X.
1. 5,0 = b 0 +1,5 b 1 ; 5. 9,5 = b0 + 8,5 b1 ;
2. 4,5 = b 0 + 4,0 b 1 ; 6. 9,0 = b0 + 10,0 b1 ;
3. 7,0 = b0 + 5,0 b1 ; 7. 11,0 = b0 + 11,0 b1 ;
4. 6,5 = b0 + 7,0 b1 ; 8. 9,0 = b0 + 12,5 b1 .
2. Суммируем результаты в каждом столбце, получаем разность значений от этих двух сумм и рассчитываем угловой коэффициент уравнения прямой регрессии b1(yх)
23,0 = 4,0 b0 + 17,5 b1 ; 38,5 = 4,0 b0 + 42,0b1 ;
23,0 = 4,0 b0 + 17,5 b1 ;
15,5 = 24,5 b1(yх) ;
b1(yх) = 15,5/24,5 = 0,633;
3. Складываем результатысумм двух столбцов, получаемуравнениев которое подставляем b1(yх) = 0,633 и рассчитываем b0 (ух)
61,5 = 8,0 b0 + 59,5х0,633; 8,0 b0 = 61,5 – 37,66 = 23,84;
b0 (ух) = 23,84/8 = 2,98;
4. Определяем расчетные значения YP, абсолютные отклонения экспериментальных значений от расчетных ΔY, а также квадраты этих отклонений ΔY² и сводим их в таблицу 2:
Ур = 2,98 + 0,63 X.
У1р = 2,98 + 0,63 × 1,5 = 3,93;
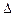 Y1 = У1 эк - У1 р = 5,0 – 3,93 = 1,07;
Y1 = У1 эк - У1 р = 5,0 – 3,93 = 1,07; 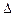 Y12 = 1,1449;
Y12 = 1,1449;
У2р = 2,98 + 0,63 х 4,0 = 5,50;
-..- -..- -..- -..- -..- -..-
У8 = 2,98 + 0,63 х 12,5 = 10,86.
5. Составляем систему уравнений из двух групп для уравненияобратной регрессия X = b0 (ху) + b1 (ху) У
1. 1,5 = b0 + 5,0 b1 ; 5. 8,5 = b0 + 9,5 b1 ;
2. 4,0 = b0 +4,5 b1 ; 6. 10,0 = b0 + 9,0 b1 ;
3. 5,0 = b 0 + 5,0 b 1 ; 7. 11,0 = b 0 + 11,0 b 1 ;
4. 7,0 = b 0 + 6,5 b 1 ; 8. 12,5 = b 0 + 9,0 b 1 .
2. Суммируем результаты в каждом столбце, получаем разность значений от этих двух сумм и рассчитываем угловой коэффициент уравнения обратной регрессии b 1(ху)
17,5 = 4,0 b 0 + 23,0 b 1 ; 42,0 = 4,0 b 0 + 38,5 b 1 ;
17,5 = 4,0 b 0 + 23,0 b 1 ;
24 ,5 = 15,5 b 1 .
b 1(ху) = 24,5/15,5 = 1,58; проверка 1,0/0,633 = 1,58.
6. Складываем результатысумм двух столбцов, получаемуравнениев которое подставляем b 1(yх) = 1,58 и рассчитываем
b 0 (ух)
59,5 = 8,0 b 0 +61,5х1,58. 8,0 b 0 = 59,5 - 61,5х1,58 = - 37,67;
b 0 (ух) = - 37,67/8 = - 4,71;
7. Определяем расчетные значения Х р, абсолютные отклонения экспериментальных значений от расчетных Δ X, а также квадраты этих отклонений Δ X ² и сводим их в таблицу 2:
X р = - 4,71 + 1,58 У.
X 1р = - 4,71 + 1,58×5,0 = 3,19;
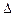 X 1 = 1,5 – 3,19 = - 1,69;
X 1 = 1,5 – 3,19 = - 1,69; 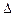 X 12 = 2,3856;
X 12 = 2,3856;
X 2р = - 4,71 + 1,58×4,5 = 2,40;
-..- -..- -..- -..- -..- -..-
X 8р = - 4,71 + 1,58×9,0 = 9,51.
8. Наносим линии прямой и обратной регрессии на рис.1 и обозначаем коэффициенты уравнений.
Метод наименьших квадратов
Например, имеем 8 пар измерений из предыдущих примеров (см. табл.2).
Х: 1,5; 4,0; 5,0; 7,0; 8,5; 10,0; 11,0; 12,5.
Y:5,0; 4,5; 7,0; 6,5; 9,5; 9,0; 11,0; 9,0.
1. Определяем расчетные значения и заполняем таблицу 2:
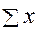 = 1,5+4,0+5,0+7,0+8,5+10,0+11,0+12,5 = 59,5;
= 1,5+4,0+5,0+7,0+8,5+10,0+11,0+12,5 = 59,5;
 = 5,0+4,5+7,0+6,5+9,5+9,0+11,0+9,0 = 61,5;
= 5,0+4,5+7,0+6,5+9,5+9,0+11,0+9,0 = 61,5;
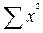 = 2,25+16,0+25,0+49,0+72,25+100,0+121,0+156,25 = 541,75;
= 2,25+16,0+25,0+49,0+72,25+100,0+121,0+156,25 = 541,75;
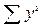 = 25,0+20,25+49,0+42,25+90,25+81,0+121,0+81,0 = 509,75;
= 25,0+20,25+49,0+42,25+90,25+81,0+121,0+81,0 = 509,75;
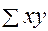 = 7,5+18,0+35,0+45,5+80,75+90,0+121,0+112,5 = 510,25;
= 7,5+18,0+35,0+45,5+80,75+90,0+121,0+112,5 = 510,25;
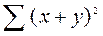 =42,25+72,25+144,0+182,25+324,0+361,0+484,0+
=42,25+72,25+144,0+182,25+324,0+361,0+484,0+
+462,25 = 2072,0.
2. Определяем центр массива экспериментальных данных (опорную точку) средние значения
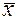 =
= 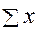 /n = 59,5/8 = 7,44 и
/n = 59,5/8 = 7,44 и 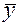 =
=  / n = 61,5/8 = 7,69.
/ n = 61,5/8 = 7,69.
3. Проверяем правильность вычислений
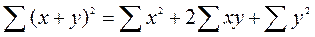 .
.
2072,0 = 541,75+2×510,25+509,75 =2072,0.
Прямая регрессия
1. Вычисляем коэффициенты уравнения линии прямой регрессии:
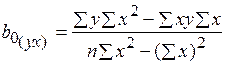 =
=
= 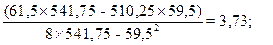
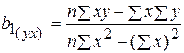 =
=
= 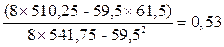
2. Определяем промежуточные величины для проверки значимости коэффициентов регрессии и оценки адекватности уравнения:
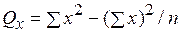 = 541,75–(59,52/8)= 99,22;
= 541,75–(59,52/8)= 99,22;
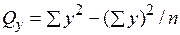 = 509,75 – (61,52/8) = 36,97;
= 509,75 – (61,52/8) = 36,97;
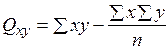 =510,25–(59,5х61,5)/8= 52,84;
=510,25–(59,5х61,5)/8= 52,84; 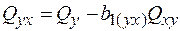 = 36,97 – 0,53х52,84 = 8,96;
= 36,97 – 0,53х52,84 = 8,96;
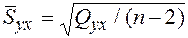 =
= 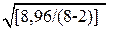 = 1,22;
= 1,22; 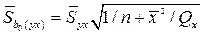 =
= 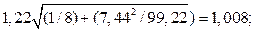
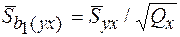 = 1,22 /
= 1,22 / 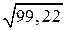 = 0,122.
= 0,122.
3. Проверяем правильность вычислений
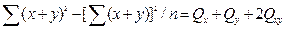
2072 – 1212/8 = 99,22 + 36,97 + 2×52,84; 241,87 = 241,87.
b 1 (ух) = Qху / Qх = 52,84/99,22 = 0,53;
b 0 (ух) = 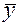 - b1 (ух)
- b1 (ух) 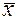 = 7,69 – 0,53×7,44 = 3,73
= 7,69 – 0,53×7,44 = 3,73
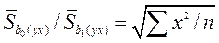 = 1,008/0,122 =
= 1,008/0,122 = 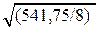 ;
;
8,2 = 8,2.
4. Проверяем статистическую значимость коэффициентов регрессии по критерию Стъюдента
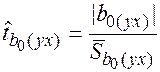 =
= 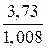 = 3,73 > 2,447,
= 3,73 > 2,447,
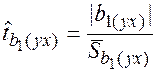 =
= 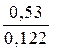 = 4,34 > 2,447.
= 4,34 > 2,447.
Если расчетные значения больше табличных


