 |
Формация. Произведение формаций
|
|
|
|
Содержание
Введение
1 Формация. Произведение формаций
2 Операции на классах групп
3 Экраны
3.1 Экраны формации
3.2 Формация с однородным экраном
4 Локальная формация
5 Построение локальных формаций
6 Локальные формации с заданными свойствами
Заключение
Литература
Введение
Формации, т.е. классы групп, замкнутые относительно фактор-групп и подпрямых произведений, всегда находились в поле деятельности исследователей по теории конечных групп. Однако вплоть до 1963 г. формационное развитие теории конечных групп шло лишь по пути накопления фактов, относящихся к различным конкретным формациям, из которых наиболее популярными были формация разрешимых групп и ее подформации, составленные из абелевых, нильпотентных и сверхразрешимых групп.
В курсовой работе рассматривается произведение формаций, операции на классах групп, приводящие к формациям. Рассматриваются локальные формации и экраны. Рассматриваются простейшие свойства локальной формации всех групп с нильпотентным компонентом.
Формация. Произведение формаций
Определение 1.1 Классом групп называют всякое множество групп, содержащее вместе с каждой своей группой  и все группы, изоморфные
и все группы, изоморфные  .
.
Если группа (подгруппа) принадлежат классу 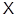 , то она называется
, то она называется 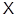 -группой (
-группой (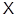 -подгруппой).
-подгруппой).
Определение 1.2. Класс групп 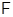 называется формацией, если выполняются следующие условия:
называется формацией, если выполняются следующие условия:
1) каждая фактор-группа любой группы из 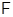 также принадлежит
также принадлежит 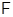 ;
;
2) из 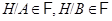 всегда следует
всегда следует 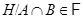 .
.
Если формации 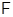 и
и  таковы, что
таковы, что  , то
, то  называется подформацией формации
называется подформацией формации 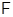 .
.
По определению, пустое множество является формацией (пустая формация). Множество 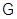 всех групп является, конечно, формацией. Единичная формация
всех групп является, конечно, формацией. Единичная формация 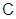 – это непустой класс групп, состоящий лишь из единичных групп. Формациями являются: класс
– это непустой класс групп, состоящий лишь из единичных групп. Формациями являются: класс 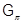 всех
всех 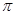 -групп, класс
-групп, класс 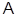 всех абелевых групп, класс
всех абелевых групп, класс 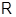 всех нильпотентных групп, класс
всех нильпотентных групп, класс 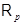 всех
всех  -групп (
-групп ( – фиксированное простое число), класс
– фиксированное простое число), класс 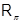 всех нильпотентных
всех нильпотентных 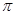 -групп, класс
-групп, класс 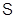 всех разрешимых групп, класс
всех разрешимых групп, класс 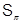 всех разрешимых
всех разрешимых 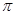 -групп. Мы привели пока лишь примеры тех формаций, за которыми закреплены соответствующие обозначения.
-групп. Мы привели пока лишь примеры тех формаций, за которыми закреплены соответствующие обозначения.
|
|
|
Лемма 1.1. Справедливы следующие утверждения:
1) пересечение любого множества формаций также является формацией;
2) если 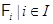 – некоторое множество формаций, линейно упорядоченное относительно включения
– некоторое множество формаций, линейно упорядоченное относительно включения 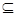 , то объединение
, то объединение  является формацией.
является формацией.
Доказательство осуществляется проверкой.
Определение 1.3. Пусть 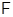 – непустая формация. Обозначим через
– непустая формация. Обозначим через 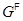 и назавем
и назавем 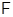 - корадикалом группы
- корадикалом группы  пересечение всех тех нормальных подгрупп
пересечение всех тех нормальных подгрупп 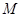 из
из  , для которых
, для которых 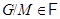 .
.
Очевидно,  -корадикал любой группы является характеристической подгруппой.
-корадикал любой группы является характеристической подгруппой.  -корадикал группы
-корадикал группы  обозначают иначе через
обозначают иначе через 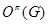 и называют
и называют 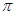 -корадикалом.
-корадикалом. 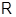 -корадикал будем называть нильпотентным радикалом; понятны также термины разрешимый корадикал,
-корадикал будем называть нильпотентным радикалом; понятны также термины разрешимый корадикал, 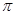 -разрешимый корадикал,
-разрешимый корадикал, 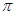 - сверхразрешимый корадикал и т.д.
- сверхразрешимый корадикал и т.д. 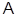 -корадикал (или абелев корадикал) – это коммутант группы. Так же как и коммутант,
-корадикал (или абелев корадикал) – это коммутант группы. Так же как и коммутант, 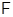 -корадикал сохраняется при гомоморфизмах.
-корадикал сохраняется при гомоморфизмах.
Лемма 1.2. Пусть 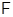 – непустая формация,
– непустая формация, 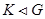 . Тогда справедливы следующие утверждения:
. Тогда справедливы следующие утверждения:
1) 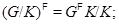
2) если  то
то 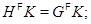
3) если 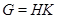 и
и 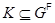 , то
, то 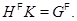
Доказательство. Пусть  . Тогда
. Тогда

Отсюда следует, что 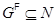 . С другой стороны,
. С другой стороны,
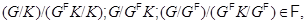
откуда получаем 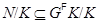 . Из
. Из  и
и 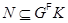 следует равенство
следует равенство  . Утверждение 1) доказано.
. Утверждение 1) доказано.
Пусть 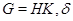 – естественный гомоморфизм группы
– естественный гомоморфизм группы 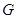 на
на  Очевидно,
Очевидно,
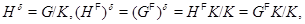
откуда следует равенство 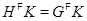 . В частности, если
. В частности, если 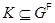 , то
, то 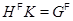 . Лемма доказана.
. Лемма доказана.
Определение 1.4. Пусть 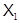 и
и 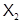 – некоторые формации. Если
– некоторые формации. Если 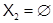 , то положим
, то положим 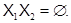 Если
Если 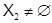 , то обозначим через
, то обозначим через 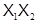 класс всех тех групп
класс всех тех групп 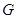 , для которых
, для которых  Класс
Класс 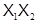 называется произведением формаций
называется произведением формаций 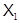 и
и 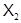 .
.
|
|
|
Из определения 1.4 следует, что произведение формаций 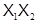 является пустой формацией тогда и только тогда, когда по крайней мере одна из формаций
является пустой формацией тогда и только тогда, когда по крайней мере одна из формаций 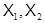 является пустой. Можно определить произведение нескольких формаций как результат последовательного умножения. Если задан упорядоченный набор формаций
является пустой. Можно определить произведение нескольких формаций как результат последовательного умножения. Если задан упорядоченный набор формаций 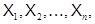 причем произведение
причем произведение 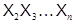 уже определено, то
уже определено, то 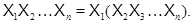 В частности, если
В частности, если 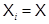 для любого
для любого 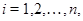 то мы приходим к понятию степени
то мы приходим к понятию степени 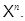
Понятие произведения формаций представляет интерес с точки зрения построения формаций.
Теорема 1.1. Произведение любых двух формаций также является формацией.
Лемма 1.3. Пусть 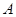 и
и 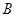 – нормальные подгруппы группы
– нормальные подгруппы группы 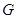 . Тогда каждый главный фактор группы
. Тогда каждый главный фактор группы 
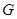 -изоморфен либо некоторому главному фактору группы
-изоморфен либо некоторому главному фактору группы 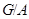 , либо некоторому главному фактору группы
, либо некоторому главному фактору группы 
Доказательство вытекает из рассмотрения 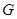 -изоморфизма
-изоморфизма 
Теорема 1.2. Пусть  – некоторая формация,
– некоторая формация,  – класс всех тех групп, все главные факторы которых принадлежат
– класс всех тех групп, все главные факторы которых принадлежат  Пусть
Пусть  – объединение формаций
– объединение формаций 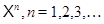 Тогда
Тогда  – подформация формации
– подформация формации 
Доказательство. Из леммы 1.3 выводим, что  – формация. Из теоремы 1.1 и леммы 1.1 вытекает, что класс
– формация. Из теоремы 1.1 и леммы 1.1 вытекает, что класс  является формацией. Если
является формацией. Если 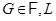 – минимальная нормальная подгруппа группы
– минимальная нормальная подгруппа группы 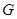 , то по индукции
, то по индукции  для некоторого натурального
для некоторого натурального 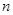 . Но тогда либо
. Но тогда либо 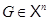 , либо
, либо 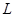 –
– 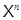 -корадикал группы
-корадикал группы 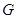 . Так как
. Так как 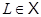 , то отсюда вытекает, что
, то отсюда вытекает, что  , и теорема доказана.
, и теорема доказана.
Операции на классах групп
Определение 2.1. Всякое отображение множества всех классов групп в себя называется операцией на классах групп.
Операции мы будем обозначать, как правило, прямыми большими латинскими буквами. Результат операции 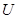 , примененной к классу
, примененной к классу  обозначается через
обозначается через  Степень операции
Степень операции 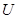 определяется так:
определяется так: 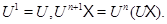 Произведение операций определяется равенствами:
Произведение операций определяется равенствами:
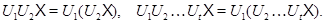
Введем операции 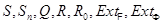 следующим образом:
следующим образом:
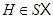 тогда и только тогда, когда
тогда и только тогда, когда 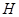 вкладывается в качестве подгруппы в некоторую
вкладывается в качестве подгруппы в некоторую  -группу;
-группу;
 тогда и только тогда, когда
тогда и только тогда, когда 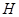 вкладывается в качестве нормальной подгруппы в некоторую
вкладывается в качестве нормальной подгруппы в некоторую  -группу;
-группу;
 тогда и только тогда, когда
тогда и только тогда, когда 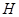 является гомоморфным образом некоторой
является гомоморфным образом некоторой  -группы;
-группы;
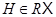 тогда и только тогда, когда
тогда и только тогда, когда 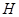 совподает с произведением некоторого конечного числа своих нормальных
совподает с произведением некоторого конечного числа своих нормальных  -подгрупп;
-подгрупп;
|
|
|
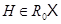 тогда и только тогда, когда
тогда и только тогда, когда 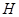 имеет нормальные подгруппы
имеет нормальные подгруппы 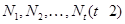 такие, что
такие, что
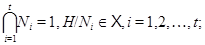
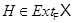 тогда и только тогда, когда
тогда и только тогда, когда 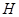 является расширением
является расширением  -группы с помощью
-группы с помощью  -группы;
-группы;
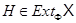 тогда и только тогда, когда
тогда и только тогда, когда 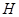 имеет нормальную подгруппу
имеет нормальную подгруппу 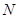 такую, что
такую, что 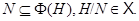
Если 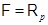 , то вместо
, то вместо 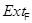 пишут
пишут  Обратим внимание на тот факт, что если
Обратим внимание на тот факт, что если  – нормальные подгруппы группы
– нормальные подгруппы группы 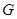 , причем
, причем  для любого
для любого  , то
, то 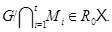 Заметим еще, что операцию
Заметим еще, что операцию 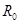 можно определить с помощью понятия подпрямого произведения. Напомним (см. Каргаполов и Мерзляков [1]), что подгруппа
можно определить с помощью понятия подпрямого произведения. Напомним (см. Каргаполов и Мерзляков [1]), что подгруппа 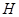 прямого произведения
прямого произведения  называется подпрямым произведением групп
называется подпрямым произведением групп  если проекция
если проекция 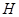 на
на 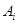 совпадает с
совпадает с 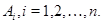 Легко видеть, что
Легко видеть, что 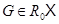 тогда и только тогда, когда
тогда и только тогда, когда 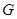 есть подпрямое произведение некоторого конечного числа
есть подпрямое произведение некоторого конечного числа  -групп.
-групп.
Определение 2.2. Класс  называется замкнутым относительно операции
называется замкнутым относительно операции 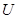 или, более коротко,
или, более коротко,  - замкнутым, если
- замкнутым, если 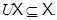
Формацию можно определить теперь как класс групп, который одновременно 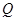 -замкнут и
-замкнут и 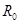 -замкнут.
-замкнут. 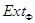 -замкнутый класс согласно Гашюцу [3] называется насыщенным.
-замкнутый класс согласно Гашюцу [3] называется насыщенным. 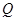 -замкнутый класс групп называется гомоморфом. Класс групп называется замкнутым относительно подгрупп (нормальных подгрупп), если он
-замкнутый класс групп называется гомоморфом. Класс групп называется замкнутым относительно подгрупп (нормальных подгрупп), если он 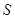 -замкнут (соответственно
-замкнут (соответственно 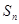 -замкнут).
-замкнут).
Лемма 2.1.  . Если класс групп
. Если класс групп  содержит единичную группу и
содержит единичную группу и 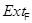 -замкнут, то
-замкнут, то 
Доказательство. Относительно операций 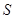 и
и  утверждение очевидно. Пусть
утверждение очевидно. Пусть  – произвольный класс групп. Ясно, что
– произвольный класс групп. Ясно, что 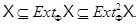 Если
Если 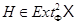 , то в
, то в 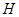 найдется нормальная подгруппа
найдется нормальная подгруппа 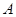 такая, что
такая, что 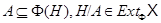 . Группа
. Группа  имеет нормальную подгруппу
имеет нормальную подгруппу  такую, что
такую, что 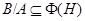 и
и 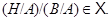 Но тогда
Но тогда 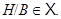 Так как
Так как 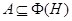 , то
, то 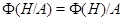 , а значит,
, а значит,  Таким образом,
Таким образом, 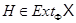 , что и требуется.
, что и требуется.
Пусть 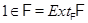 . Если
. Если 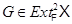 , то
, то 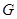 имеет нормальную
имеет нормальную  -подгруппу
-подгруппу  такую, что
такую, что 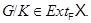 Группа
Группа 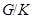 имеет нормальную
имеет нормальную  -подгруппу
-подгруппу 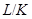 такую, что
такую, что 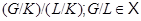 . Так как
. Так как  и
и  , то из
, то из 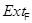 -замкнутости класса
-замкнутости класса  следует, что
следует, что  . Значит,
. Значит, 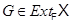 , т.е.
, т.е. 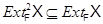 . Обратное включение очевидно.
. Обратное включение очевидно.
Лемма 2.2. Для любого класса  справедливо следующее утверждение:
справедливо следующее утверждение: 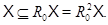
Доказательство. Если 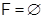 , то
, то  Пусть
Пусть  Если
Если 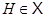 , то
, то  , а значит,
, а значит, 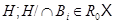 . Таким образом,
. Таким образом, 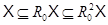 . Пусть
. Пусть  . Тогда
. Тогда 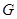 имеет такие нормальные подгруппы
имеет такие нормальные подгруппы 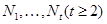 , что
, что  Группа
Группа 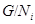 имеет такие нормальные подгруппы
имеет такие нормальные подгруппы 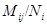 , что
, что  Так как
Так как  , то
, то 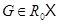 , что и доказывает равенство
, что и доказывает равенство 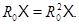
|
|
|
Лемма 2.3. Для любого класса  имеет место включение
имеет место включение 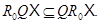
Доказательство. Если 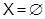 , то
, то 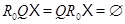 . Пусть
. Пусть 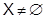 и группа
и группа  является подпрямым произведением групп
является подпрямым произведением групп 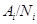 , где
, где 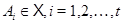 . Рассмотрим функцию
. Рассмотрим функцию 
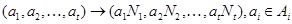 . Функция
. Функция 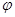 является гомоморфизмом группы
является гомоморфизмом группы  в группу
в группу 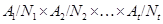 . Ясно, что
. Ясно, что

есть подпрямое произведение групп  , причем
, причем  . Следовательно,
. Следовательно,  , и лемма доказана.
, и лемма доказана.
Лемма 2.4. 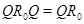
В работе Фишера, Гашюца и Хартли [1] введено следующее понятие, в некотором смысле двойственное определению формации.
Определение 2.3. Класс групп  называется классом Фиттинга, если он одновременно
называется классом Фиттинга, если он одновременно 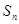 -замкнут и
-замкнут и 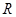 -замкнут.
-замкнут.
Класс Фиттинга мы будем в дальнейшем называть иначе радикальным классом. Ввиду двойственности (нормальная подгруппа – фактор-группа) формацию можно было бы назвать корадикальным классом.
Определение 2.4. Пусть 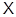 непустой
непустой  -замкнутый класс, содержащий 1. Обозначим через
-замкнутый класс, содержащий 1. Обозначим через  и назовем
и назовем 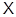 - радикалом группы
- радикалом группы  произведение всех ее нормальных
произведение всех ее нормальных 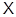 -подгрупп.
-подгрупп.
Классы 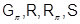 являются радикальными.
являются радикальными. 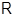 -радикал группы
-радикал группы  – это ее подгруппа Фиттинга
– это ее подгруппа Фиттинга 
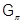 -радикал обозначают иначе через
-радикал обозначают иначе через 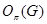 и называют
и называют  -радикалом.
-радикалом. 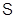 -радикал называют разрешимым радикалом; понятны также термины
-радикал называют разрешимым радикалом; понятны также термины 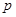 -нильпотентный радикал,
-нильпотентный радикал, 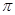 -замкнутый радикал и т.д. Класс всех
-замкнутый радикал и т.д. Класс всех  -нильпотентных групп является одновременно радикальным и корадикальным;
-нильпотентных групп является одновременно радикальным и корадикальным; 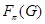 – это
– это  -нильпотентный радикал группы
-нильпотентный радикал группы 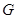 .
.
В дальнейшем мы будем изучать формации, замкнутые относительно тех или иных операций; в частности, будут рассматриваться радикальные формации, т.е. формации, являющиеся одновременно и классами Фиттинга. Сейчас мы обратимся к задаче построение формаций с помощью операций 
Теорема 2.1. Пусть 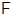 и
и 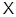 – формации, причем либо
– формации, причем либо  , либо
, либо 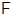 замкнута относительно нормальных подгрупп. Тогда
замкнута относительно нормальных подгрупп. Тогда  – формация, совпадающая с произведением
– формация, совпадающая с произведением 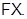
Определение 2.5. Пусть 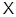 – некоторое множество групп. Пусть
– некоторое множество групп. Пусть 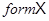 – пересечение всех тех формаций, которые содержат
– пересечение всех тех формаций, которые содержат 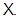 класс
класс 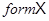 называется формацией, порожденной множеством групп
называется формацией, порожденной множеством групп 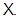
Заметим, что операцию  часто обозначают иначе через
часто обозначают иначе через  Если
Если 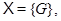 то пишут
то пишут 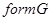 вместо
вместо  , причем в этом случае
, причем в этом случае 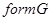 называют формацией, порожденной группой
называют формацией, порожденной группой 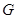 .
.
Теорема 2.2. Для любого класса 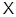 имеет место равенство:
имеет место равенство: 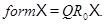
Доказательство. Если 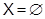 , то
, то 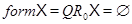 , и утверждение верно. Пусть
, и утверждение верно. Пусть  . Так как
. Так как 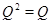 , то класс
, то класс 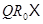 является
является 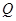 -замкнутым.
-замкнутым. 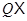 есть класс и
есть класс и 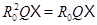 по лемме 2.2. Используя это и леммы 2.3 и 2.4, получаем
по лемме 2.2. Используя это и леммы 2.3 и 2.4, получаем
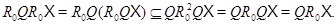
Последнее означает  -замкнутость класса
-замкнутость класса 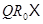 . Итак,
. Итак,  – формация, содержащая
– формация, содержащая 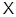 , так как
, так как 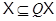 . Значит,
. Значит,  . Обратное включение очевидно.
. Обратное включение очевидно.
Лемма 2.5. Для любых элементов 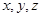 группы
группы 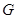 выполняются равенства
выполняются равенства  Если
Если 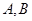 – подгруппы группы
– подгруппы группы 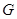 , то выполняются следующие утверждения:
, то выполняются следующие утверждения:
1) 
2) 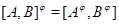 для любого гомоморфизма
для любого гомоморфизма  группы
группы  ; в частности, если группа
; в частности, если группа 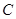 из
из 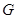 нормализует
нормализует 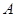 и
и 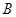 , то
, то 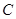 нормализует и
нормализует и 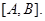
|
|
|
Лемма 2.6 Пусть 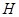 – подгруппа нильпотентной группы
– подгруппа нильпотентной группы 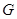 , причем
, причем 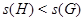 . Тогда
. Тогда 
Доказательство. Для того чтобы доказать лемму, достаточно установить, что при любом натуральном 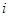 выполняется включение:
выполняется включение:

При 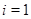 это верно, так как
это верно, так как 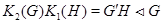 , а значит,
, а значит, 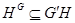 . Предположим, что включение (*) справедливо при некотором
. Предположим, что включение (*) справедливо при некотором  . Тогда, используя лемму 2.5, получаем
. Тогда, используя лемму 2.5, получаем
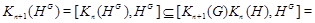
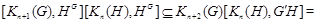
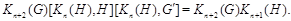
Тем самым (*) доказано.
Теорема 2.3 (Брайант, Брайс, Хартли [1]). Если  – такая подгруппа группы
– такая подгруппа группы 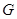 , что
, что  , то
, то 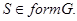
Доказательство. Пусть 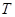 – нильпотентная нормальная подгруппа группы
– нильпотентная нормальная подгруппа группы 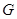 , а
, а 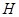 – такая подгруппа из
– такая подгруппа из 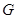 , что
, что  . Докажем индукцией по
. Докажем индукцией по  , что
, что  . Это верно, если
. Это верно, если  . Поэтому будем считать, что
. Поэтому будем считать, что 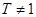 . Рассмотрим следующие подгруппы прямого произведения
. Рассмотрим следующие подгруппы прямого произведения 

Очевидно, подгруппа  нормализует
нормализует 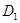 и
и  . Обозначим через
. Обозначим через 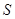 подгруппу группы
подгруппу группы 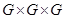 , порожденную подгруппами
, порожденную подгруппами 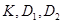 . Поскольку проекции
. Поскольку проекции 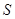 на множители прямого произведения
на множители прямого произведения 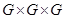 равны
равны 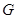 , то
, то 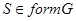 . Заметим еще, что
. Заметим еще, что 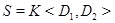 , где
, где  нормальна в
нормальна в  и нильпотентна как подпрямое произведение из
и нильпотентна как подпрямое произведение из 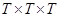 .
.
Пусть 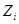 – центр подгруппы
– центр подгруппы 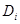 ,
, 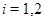 . Легко видеть, что
. Легко видеть, что  , причем
, причем 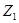 и
и  поэлементно перестановочны; аналогично,
поэлементно перестановочны; аналогично, 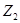 и
и 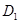 поэлементно перестановочны. Но тогда
поэлементно перестановочны. Но тогда 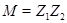 , абелева и нормальна в
, абелева и нормальна в 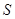 . Если
. Если 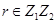 , то
, то 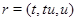 , где
, где 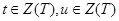 , и если
, и если 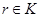 , то
, то 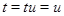 , что влечет
, что влечет  . Следовательно,
. Следовательно, 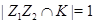 . Если
. Если 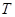 абелева, то
абелева, то  , и мы имеем
, и мы имеем
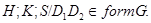
Предположим теперь, что  . Ясно, что
. Ясно, что 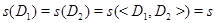 . Так как
. Так как
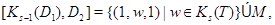
то  нильпотентна ступени
нильпотентна ступени 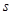 . Так как
. Так как 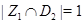 , то
, то 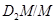 изоморфна
изоморфна  и имеет ступень
и имеет ступень  , а потому согласно лемме 2.6 ее нормальное замыкание
, а потому согласно лемме 2.6 ее нормальное замыкание  в
в  имеет ступень
имеет ступень  . Так как
. Так как  нормализует
нормализует 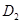 и
и 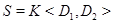 , то
, то  нормальна в
нормальна в 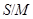 . Итак,
. Итак, 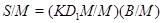 , причем
, причем 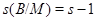 . По индукции
. По индукции

Для группы 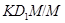 и ее нильпотентной нормальной подгруппы
и ее нильпотентной нормальной подгруппы  ступени
ступени  теорема также верна по индукции. Поэтому
теорема также верна по индукции. Поэтому
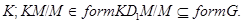
Теорема доказана.
Теорема 2.4. (Нейман [1]) Формация, порожденная разрешимой группой, содержит лишь конечное число подформаций.
Доказательство. Пусть 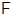 – подформация формации
– подформация формации 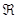 . Если
. Если 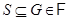 , то по теореме 2.3 имеет место
, то по теореме 2.3 имеет место 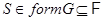 , что и требуется.
, что и требуется.
Экраны
Недостатком понятия групповой функции 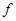 является то, что не всегда уплотнение
является то, что не всегда уплотнение 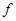 -центрального ряда нормальными подгруппами является
-центрального ряда нормальными подгруппами является 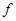 -центральным рядом.
-центральным рядом.
Определение 3.1. Отображение 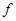 класса
класса 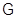 всех групп в множество классов групп назовем экраном, если для любой группы
всех групп в множество классов групп назовем экраном, если для любой группы 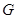 выполняются следующие условия:
выполняются следующие условия:
1)  – формация;
– формация;
2) 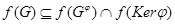 для любого гомоморфизма
для любого гомоморфизма 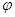 группы
группы 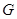 ;
;
3)  .
.
Из условия 2) вытекает, что экран 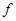 принимает одинаковое значение на изоморфных группах, т.е. является групповой функцией в смысле определения 3.1. Кроме того, видно, что если
принимает одинаковое значение на изоморфных группах, т.е. является групповой функцией в смысле определения 3.1. Кроме того, видно, что если 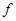 – экран, то каждый f-центральный ряд после удаления повторений может быть уплотнен до f-центрального главного ряда, а значит, класс групп, обладающих f-центральными рядами, совподает с формацией
– экран, то каждый f-центральный ряд после удаления повторений может быть уплотнен до f-центрального главного ряда, а значит, класс групп, обладающих f-центральными рядами, совподает с формацией 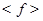 .
.
Лемма 3.1. Пусть 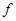 – экран,
– экран,  – группа операторов группы
– группа операторов группы  ,
, 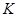 – некоторая нормальная
– некоторая нормальная 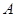 -допустимая подгруппа из
-допустимая подгруппа из 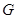 . Если
. Если 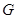 обладает нормальным
обладает нормальным 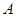 -допустимым рядом, факторы которого
-допустимым рядом, факторы которого 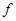 -центральны относительно
-центральны относительно 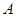 , то один из таких рядов проходит через
, то один из таких рядов проходит через  .
.
Доказательство. Пусть дан ряд, удовлетворяющий условию леммы:
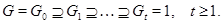
Пусть  . Тогда ряд
. Тогда ряд
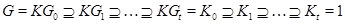
будет искомым. В этом нетрудно убедит
|
|
|


