 |
Построение локальных формаций
|
|
|
|
1. Формация всех групп. Формация  обладает локальным экраном
обладает локальным экраном 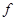 таким, что
таким, что  для любого простого
для любого простого 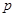 .
.
2. Формация единичных групп. Формация 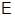 имеет пустой экран, который, очевидно, локален.
имеет пустой экран, который, очевидно, локален.
3. Формация нильпотентных 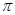 -групп. Пусть
-групп. Пусть 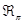 – формация всех нильпотентных
– формация всех нильпотентных 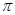 -групп,
-групп, 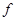 – такой локальный экран, что
– такой локальный экран, что  для любого
для любого 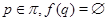 для любого
для любого  . Очевидно,
. Очевидно, 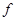 – минимальный локальный экран формации
– минимальный локальный экран формации  .
.
4. Формация 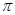 -групп. Пусть
-групп. Пусть 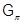 – формация всех
– формация всех 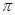 -групп,
-групп, 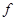 – такой локальный экран, что
– такой локальный экран, что 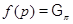 для любого
для любого  для любого
для любого 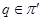 . Очевидно,
. Очевидно, 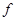 – макcимальный внутрений локальный экран формации
– макcимальный внутрений локальный экран формации  .
.
5. Формация 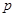 -нильпотентных групп. Пусть
-нильпотентных групп. Пусть  – формация всех
– формация всех  -нильпотентных групп (
-нильпотентных групп (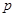 – фиксированное простое число),
– фиксированное простое число), 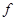 – такой локальный экран, что
– такой локальный экран, что 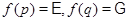 для любого простого числа
для любого простого числа  , отличного от
, отличного от  . Покажем, что
. Покажем, что 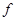 – экран формации
– экран формации  . Главный ряд
. Главный ряд 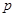 -нильпотентной группы
-нильпотентной группы 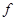 -централен. Пусть
-централен. Пусть  . Нужно установить, что
. Нужно установить, что 
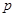 -нильпотентна. Пусть
-нильпотентна. Пусть  – минимальная нормальная подгруппа группы
– минимальная нормальная подгруппа группы  . По индукции
. По индукции 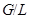
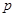 -нильпотентна. Если
-нильпотентна. Если  –
– 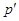 -группа, то отсюда следует, что и
-группа, то отсюда следует, что и 
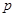 -нильпотентна. Если же
-нильпотентна. Если же 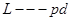 -группа, то
-группа, то  , т.е.
, т.е. 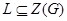 . Если теперь
. Если теперь 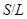 –
– 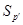 -подгруппа из
-подгруппа из 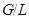 , то ввиду
, то ввиду 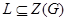 подгруппа
подгруппа 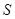
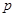 -нильпотентна, а значит, и
-нильпотентна, а значит, и 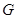
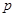 -нильпотентна. Тем самым показано, что
-нильпотентна. Тем самым показано, что  .
.
Теорема 5.1. В любой  -группе
-группе 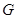 подгруппа
подгруппа 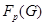 совпадает с пересечением централизаторов в
совпадает с пересечением централизаторов в 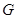 всех главных
всех главных  -факторов группы
-факторов группы 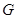 .
.
Следствие 5.1.1. В любой группе 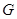 подгруппа Фиттинга
подгруппа Фиттинга  совпадает с пересечением централизаторов в
совпадает с пересечением централизаторов в 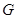 всех главных факторов группы
всех главных факторов группы 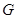 .
.
Следствие 5.1.2. Для любой 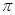 -разрешимой группы
-разрешимой группы  имеет место включение
имеет место включение  .
.
Следствие 5.1.3. (Фиттинг).  для любой разрешимой группы
для любой разрешимой группы 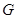 .
.
Следствие 5.1.4. (Чунихин [3]). Коммутант 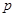 -сверхразрешимой группы
-сверхразрешимой группы  -нильпотентен.
-нильпотентен.
6. Формация 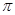 -замкнутых групп. Пусть
-замкнутых групп. Пусть  – формация всех
– формация всех 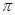 -замкнутых групп (
-замкнутых групп (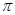 – некоторое фиксированное множество простых чисел),
– некоторое фиксированное множество простых чисел), 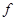 – такой локальный экран, что
– такой локальный экран, что  для любого
для любого 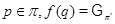 для любого
для любого  . Покажем, что
. Покажем, что 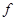 – экран формации
– экран формации  .
.
|
|
|
Очевидно,  . Предположим, что класс
. Предположим, что класс 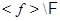 не пуст, и выберем в нем группу
не пуст, и выберем в нем группу 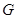 наименьшего порядка. Тогда
наименьшего порядка. Тогда 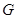 имеет единственную минимальную нормальную подгруппу
имеет единственную минимальную нормальную подгруппу 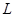 , причем
, причем 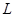 не является
не является 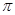 -группой. Пусть
-группой. Пусть 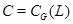 . Так как
. Так как  , то
, то  , а значит,
, а значит,  . Поэтому
. Поэтому 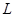 – абелева
– абелева 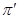 -группа. Так как
-группа. Так как 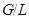
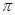 -замкнута, то и
-замкнута, то и 
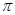 -замкнута, т.е.
-замкнута, т.е. 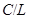 имеет нормальную
имеет нормальную  -подгруппу
-подгруппу 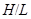 . Ясно, что
. Ясно, что 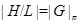 . Так как
. Так как  , то
, то 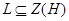 . Легко видеть, что
. Легко видеть, что 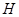 , а значит, и группа
, а значит, и группа 
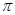 -замкнута. Тем самым показано, что
-замкнута. Тем самым показано, что 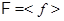 .
.
7. Формация 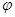 -дисперсивных групп. Пусть
-дисперсивных групп. Пусть  – некоторое линейное упорядочение множества всех простых чисел,
– некоторое линейное упорядочение множества всех простых чисел,  – формация всех
– формация всех  -дисперсивных групп. Покажем, что
-дисперсивных групп. Покажем, что  локальна.
локальна.
Рассмотрим всевозможные множества 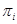 простых чисел, обладающие следующим свойством:
простых чисел, обладающие следующим свойством:  для всех
для всех 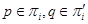 . Пусть
. Пусть 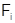 – формация всех
– формация всех  -замкнутых групп. Очевидно,
-замкнутых групп. Очевидно,  . Так как формации
. Так как формации 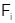 локальны, то по лемме 3.4 формация
локальны, то по лемме 3.4 формация  также является локальной.
также является локальной.
8. Формация 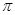 -разрешимых групп. Пусть
-разрешимых групп. Пусть  – формация всех
– формация всех 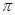 -разрешимых групп,
-разрешимых групп, 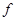 – такой локальный экран, что
– такой локальный экран, что 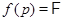 для любого простого
для любого простого  . Нетрудно заметить, что
. Нетрудно заметить, что 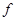 – максимальный внутрений локальный экран формации
– максимальный внутрений локальный экран формации 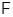 . В частности, формация
. В частности, формация 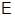 является локальной.
является локальной.
9. Формация 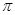 -сверхразрешимых групп. Пусть
-сверхразрешимых групп. Пусть  – формация всех
– формация всех 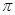 -сверхразрешимых групп. Обозначим через
-сверхразрешимых групп. Обозначим через 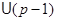 формацию всех абелевых групп экспоненты, делящей
формацию всех абелевых групп экспоненты, делящей 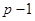 . Построим локальный экран
. Построим локальный экран 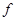 такой, что
такой, что 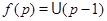 для любого
для любого  для любого
для любого  . Покажем, что
. Покажем, что 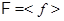 . Ясно, что
. Ясно, что  . Пусть
. Пусть  ,
, 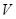 – минимальная нормальная подгруппа группы
– минимальная нормальная подгруппа группы 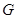 . По индукции
. По индукции 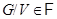 . Если
. Если 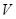 –
– 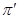 -группа, то
-группа, то 
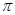 -сверхразрешима. Пусть порядок
-сверхразрешима. Пусть порядок  делится на некоторое число
делится на некоторое число 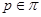 . Тогда, если
. Тогда, если 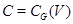 , то
, то

Отсюда следует, что 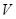 –
– 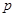 -группа.
-группа.
Лемма5.1. Пусть  – некоторая неприводимая абелева группа автоморфизмов
– некоторая неприводимая абелева группа автоморфизмов 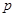 -группы
-группы 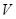 и
и  . Тогда
. Тогда  – циклическая группа порядка, делящего
– циклическая группа порядка, делящего  . Кроме того,
. Кроме того, 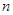 – наименьшее натуральное число, удовлетворяющее сравнению
– наименьшее натуральное число, удовлетворяющее сравнению 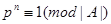 .
.
|
|
|
Доказательство. Будем считать, что 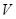 – аддитивная абелева группа. Тогда
– аддитивная абелева группа. Тогда  можно рассматривать как правое векторное пространство размерности
можно рассматривать как правое векторное пространство размерности 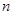 над полем
над полем 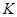 из
из 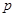 элементов. Пусть
элементов. Пусть 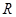 – коммутативное подкольцо кольца
– коммутативное подкольцо кольца  , порожденное элементами
, порожденное элементами  и
и 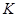 . Ввиду условия
. Ввиду условия 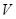 является неприводимым правым
является неприводимым правым 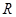 -модулем (определения, связанные с
-модулем (определения, связанные с 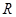 -модулями, см. у Кэртиса и Райнера [1]). По лемме Шура,
-модулями, см. у Кэртиса и Райнера [1]). По лемме Шура, 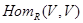 – тело. Так как
– тело. Так как 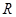 коммутативно, то
коммутативно, то  . Легко видеть, что множество всех ненулевых элементов из
. Легко видеть, что множество всех ненулевых элементов из 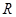 замкнуто относительно операции умножения и, следовательно, является группой. Поэтому
замкнуто относительно операции умножения и, следовательно, является группой. Поэтому 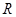 – поле. Так как
– поле. Так как 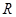 -модуль
-модуль 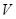 неприводим, то
неприводим, то  для любого ненулевого
для любого ненулевого 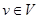 ; но тогда отображение
; но тогда отображение  , является
, является 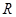 -гомоморфизмом
-гомоморфизмом 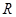 -модуля
-модуля 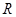 на
на  . Так как ядро
. Так как ядро 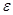 есть идеал поля
есть идеал поля 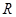 , то
, то  – изоморфизм. Следовательно,
– изоморфизм. Следовательно,  . Известно, что мультипликативная группа конечного поля циклическая. Поэтому
. Известно, что мультипликативная группа конечного поля циклическая. Поэтому 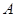 циклическая и
циклическая и  делит
делит 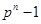 .
.
Пусть  – наименьшее натуральное число, удовлетворяющее сравнению
– наименьшее натуральное число, удовлетворяющее сравнению 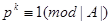 . Тогда
. Тогда  делит
делит 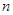 . Хорошо известно, что поле
. Хорошо известно, что поле 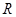 порядка
порядка  содержит подполе
содержит подполе 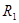 порядка
порядка  . Так как циклическая группа содержит точно одну подгруппу каждого возможного порядка и
. Так как циклическая группа содержит точно одну подгруппу каждого возможного порядка и 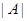 делит
делит 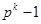 , то
, то 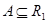 . Но тогда
. Но тогда 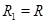 и
и 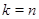 . Лемма доказана.
. Лемма доказана.
10. Формация 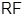 . Пусть
. Пусть 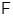 – непустая формация,
– непустая формация, 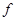 – такой локальный экран, что
– такой локальный экран, что 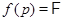 для любого простого
для любого простого 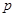 . Применяя следствие 7.1.1 можно увидеть, что
. Применяя следствие 7.1.1 можно увидеть, что 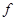 – экран формации
– экран формации 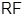 . В частности, формации
. В частности, формации  и
и 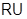 являются локальными формациями.
являются локальными формациями.
Пусть  – локальный экран некоторой подформации
– локальный экран некоторой подформации  из
из 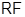 . Применяя леммы 3.3 и 4.3, видим, что
. Применяя леммы 3.3 и 4.3, видим, что  является локальным
является локальным 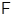 -экраном формации
-экраном формации 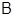 . Таким образом, каждая локальная подформация формации
. Таким образом, каждая локальная подформация формации 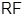 имеет внутренний локальный
имеет внутренний локальный  -экран. В частности, любая локальная подформация формации
-экран. В частности, любая локальная подформация формации  имеет внутренний локальный
имеет внутренний локальный  -экран.
-экран.
|
|
|


