 |
Локальные формации с заданными свойствами
|
|
|
|
Пусть  – некоторая операция,
– некоторая операция, 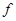 – локальный экран формации
– локальный экран формации 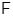 . Естественно возникают два вопроса:
. Естественно возникают два вопроса:
1) Будет ли 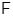
 -замкнутой, если
-замкнутой, если 
 -замкнута для любого простого
-замкнута для любого простого  ?
?
2) Будет ли 
 -замкнутой для любого простого
-замкнутой для любого простого  , если
, если 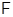
 -замкнута?
-замкнута?
Мы дадим положительный ответ на эти вопросы в некоторых конкретных случаях.
Теорема Слепова 1 Пусть  – некоторый класс групп,
– некоторый класс групп, 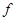 – максимальный внутренний локальный экран формации
– максимальный внутренний локальный экран формации 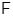 ,
,  – фиксированное простое число. Тогда справедливы следующие утверждения:
– фиксированное простое число. Тогда справедливы следующие утверждения:
1) если  , то
, то  ;
;
2) если 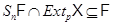 , то
, то  .
.
Доказательство. Будем доказывать оба утверждения одновременно. Пусть 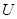 – одна из операций
– одна из операций  ,
,  . Предположим, что
. Предположим, что  . Пусть
. Пусть  – (нормальная) подгруппа группы
– (нормальная) подгруппа группы 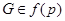 и
и  . Рассмотрим регулярное сплетение
. Рассмотрим регулярное сплетение  , где
, где  ,
,  – элементарная абелева
– элементарная абелева  -группа. По лемме 3.11
-группа. По лемме 3.11 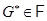 . Так как
. Так как  , то
, то  . Рассмотрим главный ряд группы
. Рассмотрим главный ряд группы  :
:

Пусть  . Так как
. Так как  и
и 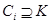 , то
, то

для любого  . Следовательно,
. Следовательно,  , где
, где  . По свойству регулярного сплетения
. По свойству регулярного сплетения  . Следовательно,
. Следовательно,  , и по лемме 3.10 () подгруппа
, и по лемме 3.10 () подгруппа  является
является  -группой. Так как
-группой. Так как  и формация
и формация  является по теореме 3.3
является по теореме 3.3  -замкнутой, то мы получаем, что
-замкнутой, то мы получаем, что 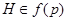 . Теорема доказана.
. Теорема доказана.
Теорема Подуфалова, Слепова 2 Пусть 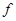 – максимальный внутренний локальный экран формации
– максимальный внутренний локальный экран формации 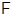 . Формация
. Формация 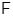
 -замкнута (
-замкнута ( -замкнута) тогда и только тогда, когда для любого простого
-замкнута) тогда и только тогда, когда для любого простого  формация
формация 
 -замкнута (соответственно
-замкнута (соответственно  -замкнута).
-замкнута).
Доказательство. Необходимость. Предположим, что 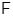
 -замкнута (
-замкнута ( -замкнута). Полагая
-замкнута). Полагая  и применяя теорему, мы получаем, что
и применяя теорему, мы получаем, что 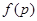
 -замкнута (
-замкнута ( -замкнута) для любого простого
-замкнута) для любого простого  .
.
Достаточность. Пусть для любого простого  формация
формация  является
является  -замкнутой (
-замкнутой ( -замкнутой). Пусть
-замкнутой). Пусть 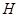 – подгруппа (нормальная подгруппа) неединичной группы
– подгруппа (нормальная подгруппа) неединичной группы  . Покажем, что
. Покажем, что  . Так как
. Так как  , то
, то 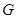 обладает
обладает 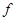 -центральным главным рядом
-центральным главным рядом
|
|
|
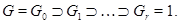
Пусть  . Так как
. Так как

то  , где
, где  . Пусть
. Пусть 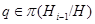 . По условию
. По условию  и
и  . Отсюда, ввиду
. Отсюда, ввиду  , вытекает, что
, вытекает, что  . Тем самым установлено, что ряд
. Тем самым установлено, что ряд

является 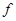 -центральным рядом группы
-центральным рядом группы 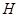 . Теорема доказана.
. Теорема доказана.
Для любого натурального числа 
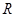 -замкнутый класс
-замкнутый класс  содержит, по определению, каждую группу
содержит, по определению, каждую группу  , представимую в виде произведения
, представимую в виде произведения  нормальных
нормальных  -подгрупп. Ослабляя это требование, мы приходим к следующему определению.
-подгрупп. Ослабляя это требование, мы приходим к следующему определению.
Определение. Класс групп  назовем слабо
назовем слабо  -замкнутым,
-замкнутым,  , если
, если  содержит всякую группу
содержит всякую группу  , имеющую
, имеющую  нормальных
нормальных  -подгрупп с попарно взаимно простыми индексами.
-подгрупп с попарно взаимно простыми индексами.
Легко заметить, что если  и
и  – подгруппы группы
– подгруппы группы 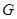 причем
причем  и
и  взаимно просты, то
взаимно просты, то 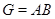 .
.
Теорема Слепова 3 Пусть 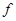 – локальный экран формации
– локальный экран формации 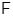 и пусть для некоторого натурального числа
и пусть для некоторого натурального числа  выполняется следующее условие: для любого простого
выполняется следующее условие: для любого простого  формация
формация  либо совпадает с
либо совпадает с  , либо входит в
, либо входит в 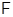 и является слабо
и является слабо  -замкнутой. Тогда
-замкнутой. Тогда  слабо
слабо  -замкнута.
-замкнута.
Доказательство. Предположим, что теорема неверна. Тогда существуют группы, не входящие в  , но имеющие
, но имеющие  нормальных
нормальных 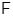 -подгрупп с попарно взаимно простыми индексами. Выберем среди всех таких групп группу
-подгрупп с попарно взаимно простыми индексами. Выберем среди всех таких групп группу 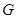 наименьшего порядка. Таким образом,
наименьшего порядка. Таким образом, 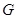 не принадлежит
не принадлежит 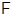 , но имеет нормальные
, но имеет нормальные 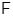 -подгруппы
-подгруппы  с попарно взаимно простыми индексами. Ясно, что все подгруппы
с попарно взаимно простыми индексами. Ясно, что все подгруппы 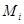 неединичны.
неединичны.
Пусть 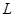 – минимальная нормальная подгруппа группы
– минимальная нормальная подгруппа группы 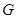 . В
. В 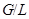 подгруппы
подгруппы  имеют попарно взаимно простые индексы и принадлежат
имеют попарно взаимно простые индексы и принадлежат  . Так как для
. Так как для 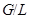 теорема верна, то
теорема верна, то  . Ясно, что
. Ясно, что 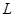 – единственная минимальная нормальная подгруппа группы
– единственная минимальная нормальная подгруппа группы  , причем
, причем  и
и 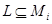 для любого
для любого  . Ввиду теоремы 4.3
. Ввиду теоремы 4.3  . Так как
. Так как  , то найдется такое
, то найдется такое  , что
, что 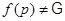 . Рассмотрим
. Рассмотрим  , где
, где  пробегает все
пробегает все  -главные факторы группы
-главные факторы группы  . Так как
. Так как 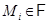 , то
, то  ,
,  . Возможны два случая.
. Возможны два случая.
Случай 1. Пусть  . Тогда
. Тогда  неабелева и
неабелева и  . Отсюда и из единственности
. Отсюда и из единственности 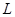 вытекает, что
вытекает, что  . Но тогда
. Но тогда  и, следовательно,
и, следовательно,  можно рассматривать как некоторую группу автомор – физмов группы
можно рассматривать как некоторую группу автомор – физмов группы  , действующую тождественно на всех
, действующую тождественно на всех 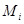 -главных факторах группы
-главных факторах группы  . По хорошо известной теореме Ф. Холла
. По хорошо известной теореме Ф. Холла  нильпотентна. Так как
нильпотентна. Так как  к тому же нормальна в
к тому же нормальна в  , то
, то  . Но тогда
. Но тогда  для любого
для любого  , а так как формация
, а так как формация  слабо
слабо  -замкнута по условию, то
-замкнута по условию, то  . Но тогда
. Но тогда  , так как
, так как 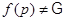 и по условию
и по условию  . Получили противоречие.
. Получили противоречие.
|
|
|
Случай 2. Пусть  . Тогда
. Тогда 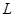 входит в
входит в  и является
и является  -группой. Так как
-группой. Так как  , то
, то  абелева. Пусть
абелева. Пусть 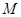 – максимальная подгруппа группы
– максимальная подгруппа группы 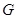 , не содержащая
, не содержащая  . Тогда
. Тогда  ,
,  ,
,  ,
, 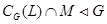 . Отсюда, ввиду единственности
. Отсюда, ввиду единственности 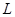 , заключаем, что
, заключаем, что  , a значит,
, a значит,  . По лемме 3.10
. По лемме 3.10  является
является  -группой. Но тогда и
-группой. Но тогда и  является
является  -группой, причем
-группой, причем  . Мы получаем, таким образом, что
. Мы получаем, таким образом, что 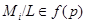 для любого
для любого  . Но тогда
. Но тогда  , так как
, так как  слабо
слабо  -замкнута. Последнее означает, что
-замкнута. Последнее означает, что 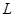
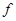 -центральна в
-центральна в  , что противоречит равенству
, что противоречит равенству  . Снова получили противоречие.
. Снова получили противоречие.
Теорема доказана.
Следствие 4 Пусть группа 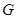 имеет две нормальные
имеет две нормальные  -сверхразрешимые подгруппы, индексы которых взаимно просты. Тогда
-сверхразрешимые подгруппы, индексы которых взаимно просты. Тогда 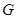
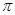 -сверхразрешима.
-сверхразрешима.
Для того чтобы получить это следствие, достаточно заметить, что построенный экран удовлетворяет условию теоремы при  .
.
Следствие 5 Пусть группа  имеет две нормальные сверхразрешимые подгруппы, индексы которых взаимно просты. Тогда
имеет две нормальные сверхразрешимые подгруппы, индексы которых взаимно просты. Тогда 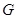 сверхразрешима.
сверхразрешима.
Теорема Слепова 6 Пусть формация  имеет такой локальный экран
имеет такой локальный экран 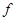 , что для любого простого
, что для любого простого  формация
формация  либо совпадает с
либо совпадает с  , либо входит в
, либо входит в 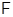 и является
и является 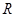 -замкнутой. Тогда
-замкнутой. Тогда 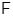
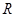 -замкнута.
-замкнута.
Доказательство. Повторяем с очевидными изменениями доказательство теоремы.
Теорема Слепова 7 Пусть 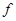 – максимальный внутренний локальный экран формации
– максимальный внутренний локальный экран формации  . Формация
. Формация 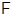
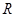 -замкнута (слабо
-замкнута (слабо  -замкнута,
-замкнута,  ) тогда и только тогда, когда для любого простого
) тогда и только тогда, когда для любого простого  формация
формация 
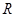 -замкнута (соответственно слабо
-замкнута (соответственно слабо  -замкнута).
-замкнута).
Доказательство. Достаточность вытекает из теорем и. Пусть 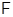
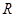 -замкнута (слабо
-замкнута (слабо  -замкнута,
-замкнута,  ). Пусть
). Пусть  , где
, где  – нормальные
– нормальные 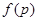 -подгруппы (нормальные
-подгруппы (нормальные  -подгруппы с попарно взаимно простыми индексами). Так как
-подгруппы с попарно взаимно простыми индексами). Так как  , то
, то  . Покажем, что
. Покажем, что 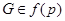 .
.
Пусть  , где
, где  ,
,  – элементарная абелева
– элементарная абелева  -группа. По лемме 3.11
-группа. По лемме 3.11  для любого
для любого  . Так как
. Так как 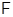
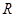 -замкнута (слабо
-замкнута (слабо  -замкнута), то отсюда вытекает, что
-замкнута), то отсюда вытекает, что  . Если
. Если  – пересечение централизаторов в
– пересечение централизаторов в  всех
всех  -главных факторов группы
-главных факторов группы  , то
, то

Так как  , то по лемме 3.10 подгруппа
, то по лемме 3.10 подгруппа  является
является  -группой. Но тогда
-группой. Но тогда 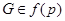 , так как по теореме 3.3 имеет место равенство
, так как по теореме 3.3 имеет место равенство 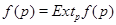 .
.
Теорема доказана.
|
|
|
Лемма Чунихин 8 Пусть  ,
, 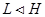 ,
, 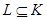 . Тогда
. Тогда  . В частности, если
. В частности, если  и
и  , то
, то  непростая.
непростая.
Доказательство. Из равенства 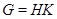 следует, что
следует, что

Следовательно,  . Отсюда, ввиду
. Отсюда, ввиду  для любого
для любого 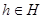 , получаем
, получаем 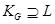 . Лемма доказана.
. Лемма доказана.
Теорема Виландт 9 Группа 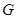 разрешима, если она имеет три разрешимые подгруппы, индексы которых в
разрешима, если она имеет три разрешимые подгруппы, индексы которых в 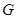 попарно взаимно просты.
попарно взаимно просты.
Доказательство. Пусть группа 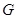 имеет разрешимые подгруппы
имеет разрешимые подгруппы  ,
,  и
и  с попарно взаимно простыми индексами. Тогда
с попарно взаимно простыми индексами. Тогда  . Пусть
. Пусть  – минимальная нормальная подгруппа из
– минимальная нормальная подгруппа из  . Так как
. Так как  разрешима, то
разрешима, то  ,
,  – простое число. Ввиду условия теоремы,
– простое число. Ввиду условия теоремы,  не делит одновременно
не делит одновременно  и
и  . Пусть, для определенности,
. Пусть, для определенности,  не делит
не делит  . Это значит, что силовская
. Это значит, что силовская  -подгруппа из
-подгруппа из  является силовской
является силовской  -подгруппой группы
-подгруппой группы 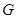 . Ввиду теоремы Силова
. Ввиду теоремы Силова  , где
, где  . Так как
. Так как  и
и 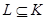 , то по лемме
, то по лемме  . Таким образом,
. Таким образом, 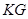 – неединичная разрешимая нормальная подгруппа группы
– неединичная разрешимая нормальная подгруппа группы 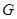 . В фактор-группе
. В фактор-группе  индексы подгрупп
индексы подгрупп  ,
,  и
и  попарно взаимно просты. По индукции
попарно взаимно просты. По индукции 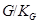 разрешима, но тогда и
разрешима, но тогда и  разрешима. Теорема доказана.
разрешима. Теорема доказана.
Следуя Крамеру, введем следующее определение.
Определение. Класс групп  называется
называется  -замкнутым (
-замкнутым ( – натуральное число), если
– натуральное число), если  содержит всякую группу
содержит всякую группу  , имеющую
, имеющую 
 -подгрупп, индексы которых в
-подгрупп, индексы которых в 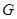 при
при  попарно взаимно просты.
попарно взаимно просты.
По определению, пустая формация  -замкнута для любого
-замкнута для любого  . Единственной
. Единственной  -замкнутой непустой формацией, отличной от
-замкнутой непустой формацией, отличной от  , условимся считать
, условимся считать 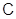 .
.
Лемма 10 Пусть  и
и  –
–  -замкнутые классы групп. Тогда
-замкнутые классы групп. Тогда  также
также  -замкнут.
-замкнут.
Доказательство очевидно.
Следующая лемма доказана Крамером.
Лемма 11 Пусть формация  содержится в
содержится в 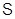 и
и  -замкнута,
-замкнута,  . Тогда формация
. Тогда формация  является
является  -замкнутой.
-замкнутой.
Доказательство. Пусть группа  имеет
имеет 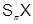 -подгруппы
-подгруппы  ,
,  ,…,
,…,  , индексы которых в
, индексы которых в 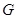 попарно взаимно просты. Так как
попарно взаимно просты. Так как  , то по теореме группа
, то по теореме группа  разрешима. При любом гомоморфизме группы
разрешима. При любом гомоморфизме группы  образы подгруппы
образы подгруппы  принадлежат
принадлежат 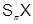 и имеют попарно взаимно простые индексы. Поэтому можно считать, что
и имеют попарно взаимно простые индексы. Поэтому можно считать, что  -корадикал
-корадикал  группы
группы 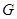 является ее единственной минимальной нормальной подгруппой. Ясно, что
является ее единственной минимальной нормальной подгруппой. Ясно, что 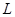 является
является  -группой для некоторого
-группой для некоторого  . Подгруппа Фиттинга
. Подгруппа Фиттинга 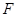 группы
группы  также является
также является  -группой. Индекс любой подгруппы, не содержащей
-группой. Индекс любой подгруппы, не содержащей  , делится на
, делится на  . Поэтому
. Поэтому  содержится по крайней мере в
содержится по крайней мере в  подгруппах нашей системы подгрупп
подгруппах нашей системы подгрупп  . Будем считать, что
. Будем считать, что 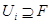 ,
,  . Так как
. Так как  является
является  -группой, то
-группой, то  и
и  поэлементно перестановочны,
поэлементно перестановочны,  . Отсюда и из следствия вытекает, что
. Отсюда и из следствия вытекает, что  ,
,  . Так как
. Так как  , то мы получаем, что
, то мы получаем, что  ,
,  . Воспользовавшись
. Воспользовавшись  -замкнутостью формации
-замкнутостью формации  , мы приходим к тому, что
, мы приходим к тому, что 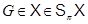 .
.
|
|
|
Лемма доказана.
Теорема Крамер 12 Пусть 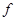 – такой локальный
– такой локальный 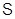 -экран формации
-экран формации  , что для любого простого
, что для любого простого  формация
формация 
 -замкнута,
-замкнута,  . Тогда
. Тогда 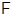
 -зaмкнута.
-зaмкнута.
Доказательство. Так как 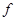 –
– 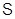 -экран, то
-экран, то  для любого простого
для любого простого  , а значит,
, а значит,  . Пусть
. Пусть  . Ввиду леммы 4.5
. Ввиду леммы 4.5  . Если
. Если  , то
, то 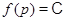 и
и 
 -замкнута; если же
-замкнута; если же  , то по лемме формация
, то по лемме формация 
 -замкнута. В любом случае
-замкнута. В любом случае 
 -замкнута. По лемме
-замкнута. По лемме 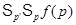
 -замкнута. Применяя лемму, мы видим, что и формация
-замкнута. Применяя лемму, мы видим, что и формация 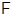
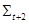 -замкнута. Теорема доказана.
-замкнута. Теорема доказана.
Так как формация  имеет единичный экран, удовлетворяющий условию теоремы при
имеет единичный экран, удовлетворяющий условию теоремы при  , то мы получаем
, то мы получаем
Следствие Кегель 13 Группа 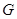 нилъпотентна, если она имеет три нилъпотентные подгруппы, индексы которых в
нилъпотентна, если она имеет три нилъпотентные подгруппы, индексы которых в 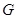 попарно взаимно просты.
попарно взаимно просты.
Этот факт вытекает также и из следующего результата Кегеля.
Лемма 14 Класс всех  -замкнутых групп
-замкнутых групп  -замкнут.
-замкнут.
Доказательство такое же, как и у теоремы.
Лемма 15 Каждая формация нилъпотентных групп является  -замкнутой.
-замкнутой.
Доказательство. Пусть  – некоторая формация нильпотентных групп. Пусть группа
– некоторая формация нильпотентных групп. Пусть группа  имеет
имеет  -подгруппы
-подгруппы  ,
,  и
и  с попарно взаимно простыми индексами. Тогда по следствию группа
с попарно взаимно простыми индексами. Тогда по следствию группа 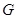 нильпотентна. Если
нильпотентна. Если  – наивысшая степень простого числа
– наивысшая степень простого числа  , делящая
, делящая  , то
, то  делит
делит  для некоторого
для некоторого  , так как
, так как  не может делить одновременно индексы всех подгрупп
не может делить одновременно индексы всех подгрупп  ,
,  и
и  . Если
. Если  делит
делит  , то силовская
, то силовская  -подгруппа
-подгруппа 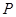 из
из  входит в
входит в  и является силовской
и является силовской  -подгруппой группы
-подгруппой группы 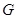 . Тем самым показано, что все силовские подгруппы нильпотентной группы
. Тем самым показано, что все силовские подгруппы нильпотентной группы  являются
являются  -группами. Так как
-группами. Так как  – формация, то отсюда следует, что
– формация, то отсюда следует, что  .
.
Лемма доказана.
Лемма 16 Пусть  – некоторый
– некоторый  -замкнутый гомоморф
-замкнутый гомоморф  -замкнутых групп. Тогда класс
-замкнутых групп. Тогда класс 
 -замкнут.
-замкнут.
Доказательство. Пусть группа  имеет
имеет  -подгруппы
-подгруппы  ,
,  и
и  с попарно взаимно простыми индексами. По лемме
с попарно взаимно простыми индексами. По лемме 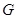 имеет нормальную силовскую
имеет нормальную силовскую  -подгруппу
-подгруппу 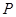 . Поскольку
. Поскольку  является силовской
является силовской  -подгруппой в
-подгруппой в  и
и  – гомоморф, то
– гомоморф, то  . В группе
. В группе  индексы подгрупп
индексы подгрупп  ,
,  и
и  попарно взаимно просты. Поэтому ввиду
попарно взаимно просты. Поэтому ввиду  -замкнутости
-замкнутости  имеем
имеем  . Лемма доказана.
. Лемма доказана.
Лемма 17 Для любого простого  и любой формации нильпотентных групп
и любой формации нильпотентных групп  класс
класс  является
является  -замкнутой формацией.
-замкнутой формацией.
Доказательство. По лемме класс 
 -замкнут. По лемме класс
-замкнут. По лемме класс 
 -замкнут и по теореме 1.1 является формацией.
-замкнут и по теореме 1.1 является формацией.
Теорема 18 Пусть  – локальная подформация формации
– локальная подформация формации  ,
,  – максимальный внутренний локальный экран формации
– максимальный внутренний локальный экран формации 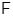 . Если для любого простого
. Если для любого простого  формация
формация 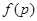
 -замкнута,
-замкнута,  , то
, то 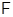
 -замкнута.
-замкнута.
|
|
|
Доказательство. Пусть  . Ввиду теоремы 3.3 и леммы 4.5,
. Ввиду теоремы 3.3 и леммы 4.5,  . Формация
. Формация 
 -замкнута. По лемме формация
-замкнута. По лемме формация 
 -замкнута. Теорема доказана.
-замкнута. Теорема доказана.
Теорема Крамер 19 Любая локальная подформация формации  является
является  -замкнутой.
-замкнутой.
Доказательство. Пусть 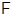 – локальная подформация формации
– локальная подформация формации  .
.  имеет внутренний локальный
имеет внутренний локальный  -экран
-экран  . Пусть
. Пусть 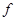 – максимальный внутренний локальный экран формации
– максимальный внутренний локальный экран формации  . Тогда по теореме 3.3 для любого простого
. Тогда по теореме 3.3 для любого простого  имеет место рав
имеет место рав
|
|
|


