 |
Задачи для самостоятельного решения
|
|
|
|
101. Пучок параллельных лучей монохроматического света с длиной волны 662 нм падает нормально на зеркальную плоскую поверхность. Мощность потока излучения 0,6 Вт. Определить силу давления, испытываемую этой поверхностью.
F = 4∙10-9 Н.
102. Параллельный пучок лучей длиной волны 500 нм падает нормально на зачерненную поверхность, производя давление 10 мкН/м2. Определить число фотонов, падающих на единицу площади в единицу времени.
N = 7,56∙1021 м-2с-1
103. Поток монохроматического излучения с длиной волны 500 нм падает нормально на плоскую зеркальную поверхность и давит на нее с силой 10-8Н. Определить число фотонов, ежесекундно падающих на эту поверхность.
N = 3,78∙1018 с-1
104. На поверхность площадью 0,01 м2 за одну секунду падает световая энергия 1,05 Дж. Найти световое давление в случаях, когда поверхность полностью отражает и полностью поглощает падающие на нее лучи.
Р1 = 0,7 мкПа; Р2 = 0, 35 мкПа
105. Монохроматический пучок света (λ =490 нм), падая по нормали к поверхности, производит световое давление 4,9 мкПа. Какое число фотонов в единицу времени падает на единицу площади этой поверхности? Коэффициент отражения равен 0,25.
N = 2,9∙1021 м-2с-1
106. В результате эффекта Комптона фотон при соударении с электроном был рассеян на угол 900. Энергия рассеянного фотона 0,4 Мэв. Определить энергию фотона до рассеяния.
Е = 1,85 Мэв
107. Фотон с энергией 0,75 Мэв рассеялся на свободном электроне под углом 600. Определить энергию рассеянного фотона.
Е = 0,43 Мэв
108. Рентгеновское излучение длиной волны 55,8 пм рассеивается плиткой графита (комптон-эффект). Определить длину волны лучей, рассеянных под углом 600 к направлению падающих лучей.
λ = 57 пм
109. Энергия рентгеновских лучей 0, 6 Мэв. Найти энергию электрона отдачи, если длина волны рентгеновских лучей после комптоновского рассеяния изменилась на 20%.
|
|
|
Е = 0,1 Мэв
110. При комптоновском рассеянии энергия падающего фотона распределяется поровну между рассеянным фотоном и электроном отдачи. Угол рассеяния 900. Найти энергию рассеянного фотона.
Е = 0,26 Мэв
ВОЛНЫ ДЕ БРОЙЛЯ
· Формула де Бройля. Частицы материи наряду с корпускулярными обладают также и волновыми свойствами (корпускулярно-волновой дуализм). Это означает, что любой частице, обладающей импульсом, соответствует волна, длина которой равна:
где 
- импульс частицы, движущейся со скоростью 
,
– масса покоя частицы.
· Релятивистский случай (скорость частицы сравнима со скоростью света). В этом случае импульс равен:
Тогда
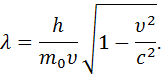
· Импульс частицы связан с ее кинетической энергией соотношениями:
в классическом случае
в релятивистском случае
где 
- кинетическая энергия частицы,
- энергия покоя частицы.
Примеры решения задач
Пример 25. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U. Найти длину волны де Бройля l для двух случаев: 1) U1 = 51 B; 2) U2 = 600 кВ.
| Дано: U1 = 51 B U2 = 600∙103 В me = 9,1∙10-31кг с = 3∙108 м/с 1 эВ = 1,6∙10-19Дж l1 -? l2 -? | Решение:
а) Найдем кинетическую энергию частицы в первом случае:
Подставив в формулу (1) численные значения физических величин, получим следующее значение кинетичекской энергии электрона:
 (2)
Эта энергия значительно меньше энергия покоя электрона:
|
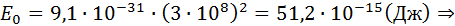
(3)
Следовательно можно использовать классический случай:
(4)
Тогда
Подставив в формулу (5) численные значения величин, учитывая также, что h = 
получим длину волны де Бройля для первого случая:
б) Найдем кинетическую энергию частицы для втрого случая:
Подставив в формулу (6) численные значения физических величин, получим следующее значение кинетичекской энергии электрона:
|
|
|
Эта энергия сравнима с энергией покоя электрона Е0 = 0,51 МэВ, поэтому надо рассматривать релятивистском случае:
Тогда длина волны l2 будет равна:
Подставляя в формулу (9) численные значения физических величин и значения (3) и (7) для 
и 
получим:
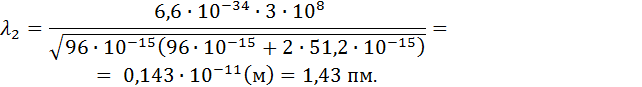
Пример 26. Баллон с гелием нагрели до температуры 800 К. Найти длину волны де Бройля для атома гелия, движущегося со средней квадратичной скоростью при данной температуре.
Дано:
Т = 800 К
 -?
| Решение:
Согласно гипотезе де Бройля для атома гелия, движущегося со средне- квадратичной скоростью  , соответствует волна, длина которой равна:
где 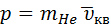 - импульс атома гелия, движущегося со средне-квадратичной скоростью ,
 – масса покоя атома гелия.
|
Массу покоя атома гелия найдем из выражения:
где 
- молярная масса газа,
- число Авогадро (количество атомов находящихся в 1 моле вещества).
Подставив в формулу (2) численные значения величин найдем массу одного атома гелия:
Согласно молекулярно - кинетической теории газов, среднеквадратичная скорость молекул равна:
где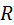 
- универсальная газовая постоянная,
Т – температура гелия в баллоне,
- молярная масса газа.
Подставив в формулу (4) численные значения величин найдем
среднеквадратичная скорость молекулы гелия:
Подставляя в формулу (1) из (3) и (5) численные значения
и найдем длину волны де Бройля для атома гелия:
|
|
|
