 |
Задачи для самостоятельного решения
|
|
|
|
Кафедра ОФиФНГП
Сборник задач по физике
И примеры их решения
ЧАСТЬ II
Самара 2015
ББК 22.5
УДК 530.1
УДК 535.(075.8)
Авторы: Т. Н. Голованова, А. М. Штеренберг
Сборник задач по физике и примеры их решения. Часть II /Голованова Т. Н., Штеренберг А. М. – Самара: Самар. гос. техн. ун-т, 2015. – 70 с. ил.
Сборник содержит основные законы и формулы, необходимые для решения задач. Даны примеры решения типовых задач и задачи для самостоятельного решения. Пособие предназначено для студентов-заочников инженерно-технических специальностей вузов. Может быть использовано студентами дневных отделений вузов.
Ил. 18. Табл. 2. Библиогр.: 7 назв.
Печатается по решению редакционно-издательского совета СамГТУ
ПРЕДИСЛОВИЕ
Сборник содержит основные законы и формулы, необходимые для решения задач. Даны примеры решения типовых задач и задачи для самостоятельного решения. Числовые данные приведены с учетом точности соответствующих величин и правил действия над приближенными числами.
Учебное пособие предназначено для оказания помощи студентам-заочникам инженерно-технических специальностей вузов при изучении курса общей физики. Может быть полезным для студентов дневных отделений вузов. Пособие составлено в соответствии с действующей программой по курсу физики для технических университетов.
Даны две таблицы вариантов контрольных работ по электродинамике с волновой оптикой (контрольная работа № 3) и квантовой оптике с атомной и ядерной физикой (контрольная работа №4). Таблицы содержат варианты для специальностей, учебными планами которых, предусмотрено по курсу физики четыре контрольных работы. Кроме того, в пособии даны методические указания к решению задач и выполнению контрольных работ, а также, справочные материалы.
|
|
|
Программа курса физики
Для инженерно -технических специальностей заочного отделения вуза
Часть II
ЭЛЕКТРОДИНАМИКА
Сила и плотность электрического тока. Закон Ома для однородного участка цепи в дифференциальной и интегральной форме. Электродвижущая сила и напряжение. Закон Ома для неоднородного участка цепи в дифференциальной и интегральной форме. Правила Кирхгофа. Закон Джоуля – Ленца.
Индукция магнитного поля. Сила Лоренца и сила Ампера. Закон Био – Савара. Контур с током в магнитном поле. Магнитный момент. Теорема Гаусса для магнитного поля. Работа при перемещении проводника стоком в магнитном поле. Молекулярные токи. Намагниченность. Напряженность магнитного поля. Пара- и диамагнетики. Ферромагнетики. Магнитный гистерезис.
Явление и закон электромагнитной индукции. Правило Ленца. Явление самоиндукции. Индуктивность. Энергия магнитного поля. Ток смещения. Система уравнений Максвелла.
Колебательный контур. Свободные незатухающие и затухающие колебания. Логарифмический декремент затухания. Вынужденные незатухающие колебания. Резонанс напряжения. Переменный электрический ток. Мощность переменного тока. Электромагнитные волны, их свойства. Энергия электромагнитных волн.
Волновая и квантовая оптика
Интерференция света. Условия интерференции. Интерференция от двух линейных когерентных источников света и в тонких пленках. Дифракция света. Принцип Гюйгенса – Френеля. Метод зон Френеля. Дифракция Френеля на круглом отверстии и диске. Дифракция Фраунгофера на одной щели и дифракционной решетке. Поляризация света. Естественный и поляризованный свет. Поляризация света при отражении и преломлении. Закон Брюстера. Двойное лучепреломление. Поляроиды и поляризационные призмы. Закон Малюса. Дисперсия света. Области нормальной и аномальной дисперсии. Фазовая и групповая скорости.
|
|
|
Тепловое излучение, его характеристики. Законы Кирхгофа и Стефана – Больцмана. Закон смещения Вина. Квантовая гипотеза и формула Планка. Внешний фотоэффект и его законы. Уравнение Эйнштейна для внешнего фотоэффекта. Фотоны. Энергия, импульс и масса фотона. Эффект Комптона. Давление света.
Атомная И Ядерная физика
Постулаты Бора. Теория Бора для атома водорода. Гипотеза и формула де Бройля. Соотношения неопределенностей. Волновая функция и ее статистический смысл. Уравнение Шредингера для стационарных состояний. Свободная частица. Туннельный эффект. Частица в одномерной, прямоугольной, бесконечно глубокой потенциальной яме. Квантование энергии и импульса частицы. Линейный гармонический осциллятор. Атом водорода. Главное, орбитальное и магнитное квантовые числа. Опыт Штерна и Герлаха. Спин электрона. Спиновое квантовое число. Фермионы и бозоны. Принцип Паули. Распределение электронов в атоме по состояниям. Спектры атомов и молекул. Поглощение, спонтанное и вынужденное излучения. Понятие о лазерах.
Состав ядра. Нуклоны. Заряд, масса и размеры атомного ядра. Массовое и зарядовое числа. Момент импульса и магнитный момент ядра. Свойства и природа ядерных сил. Дефект масс и энергия связи ядра. Закономерности и происхождение α-, β-и γ-излучений атомных ядер. Ядерные реакции и законы сохранения. Реакция деления ядер.
Цепная ядерная реакция. Понятие о ядерной энергетике. Термоядерная реакция. Элементарные частицы, их классификация и взаимопревращаемость. Фундаментальные взаимодействия.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Детлаф А. А., Яворский Б. М. Курс физики: учеб. пособие / А. А. Детлаф Б. М. Яворский. – М.: Академия, 2003. – 720 с.: ил.
2. Иродов И. Е. Электромагнетизм. Основные законы: / И. Е. Иродов. – М.: Лаборатория Базовых Знаний, 2002. – 320 с.: ил.
3. Иродов И. Е. Квантовая физика. Основные законы: – М.: Лаборатория Базовых Знаний, 2002 – 272 с.: ил.
4. Савельев И.В. Курс общей физики: кн. 2: Электричество и магнетизм: учеб. пособие /И.В. Савельев. – М.: Астрель, 2004. – 254с.
|
|
|
5. Савельев И. В. Курс общей физики: кн. 4: Волны. Оптика: учеб. пособие / И. В. Савельев. – М.: Астрель, 2002. – 256 с.: ил.
6. Савельев И. В. Курс общей физики: кн. 5: Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц: учеб. пособие / И. В. Савельев. – М.: Астрель, 2002. – 368 с.: ил.
7. Волькенштейн В. С. Сборник задач по общему курсу физики. Изд. 3-е, исп. и доп. – СПб.: Книжный мир, 2005. – 328 с.
Контрольная работа №3
Электродинамика. волновая оптика
Основные формулы
Электродинамика
1. Сила электрического тока
 , (1Ф)
, (1Ф)
где dq – элементарный заряд, переносимый через поперечное сечение проводника за время dt. Для постоянного тока
 (2Ф)
(2Ф)
2. Плотность тока
 , (3Ф)
, (3Ф)
где S – площадь поперечного сечения проводника; q 0 – заряд частицы (например, электрона); n – концентрация частиц; < v > – средняя скорость упорядоченного движения частиц.
3. Закон Ома для:
а) однородного участка цепи (не содержащего э. д. с.)
 , (4Ф)
, (4Ф)
где – U = φ1 – φ2 – напряжение или разность потенциалов на концах участка цепи; R – сопротивление участка цепи;
б) неоднородного участка цепи (содержащего э. д. с.)
I = (φ1 – φ2 +  )/ R 12, (5Ф)
)/ R 12, (5Ф)
где  – э. д. с. источника тока; R 12 – полное сопротивление участка цепи (сумма внешнего сопротивления R и внутреннего сопротивления r источника тока R 12 = R + r).
– э. д. с. источника тока; R 12 – полное сопротивление участка цепи (сумма внешнего сопротивления R и внутреннего сопротивления r источника тока R 12 = R + r).
4. Электрическое сопротивление проводника
 , (6Ф)
, (6Ф)
где ρ – удельное сопротивление, зависит от материала проводника и его температуры; l – длина проводника; S – площадь его поперечного сечения.
5. Сопротивление системы проводников при:
а) последовательном соединении
R = ∑ R i; (7Ф)
б) параллельном соединении
 , (8Ф)
, (8Ф)
где R i – сопротивление i – го проводника.
6. Законы Кирхгофа:
а) первый закон
∑ I i = 0. (9Ф)
Сумма токов в узле равна нулю. Условились силам токов, текущим к узлу, приписывать знак «плюс», а текущим от узла – «минус»;
б) второй закон
∑ I i R i = ∑  i. (10Ф)
i. (10Ф)
Сумма произведений сил токов в отдельных участках замкнутого контура на их сопротивления равна сумме э. д. с., действующих в этом контуре.
|
|
|
7. Мощность тока для однородного участка цепи
Р = I 2 R = U 2/ R. (11Ф)
Первой формулой удобно пользоваться при последовательном соединении проводников, второй – при параллельном.
8. Закон Джоуля – Ленца в интегральной и дифференциальной формах:
Q = I 2 Rt; dQ = I 2 Rdt, (12Ф)
где Q – количество теплоты, выделяемой на участке цепи сопротивлением R по которому течет ток I в течении времени t.
9. Закон Био – Савара для тонкого проводника

где dB – модульмагнитной индукции поля, создаваемого элементом dl проводника с током I;  – магнитная постоянная, находится из таблицы; α – угол между радиус – вектором r, проведенным от элемента
– магнитная постоянная, находится из таблицы; α – угол между радиус – вектором r, проведенным от элемента  к точке, где определяется магнитное поле.
к точке, где определяется магнитное поле.
10. Магнитная индукция в центре кругового тока

где R – радиус кругового витка.
11. Магнитная индукция на оси кругового тока
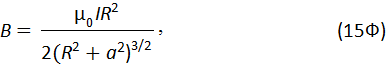
где a – расстояние от центра витка до точки, в которой вычисляется магнитная индукция.
12. Магнитная индукция поля бесконечно длинного прямолинейного проводника с током

где a – кратчайшее расстояние от оси проводника до точки, в которой вычисляется магнитная индукция.
13. Магнитная индукция поля соленоида

где n – число витков соленоида, приходящееся на единицу его длины,  – магнитная проницаемость.
– магнитная проницаемость.
14. Модуль силы, действующей на проводник с током, находящийся в магнитном поле (закон Ампера),
 (18Ф)
(18Ф)
где α – угол между направлением тока I в проводнике и магнитной индукцией B. Это выражение справедливо для однородного магнитного поля и проводника длиной dl (элемента проводника).
15. Сила взаимодействия двух параллельных проводников с токами  ,
, 

где d – расстояние между проводниками; l – длина проводников.
16. Сила Лоренца
 или
или  (20Ф)
(20Ф)
где  – скорость заряженной частицы;
– скорость заряженной частицы;  – угол между скоростью
– угол между скоростью  и магнитной индукцией
и магнитной индукцией  .
.
17. Магнитный поток через поверхность:
а) в случае однородного поля и плоской поверхности
 или
или  (21Ф)
(21Ф)
где S – площадь контура; α – угол между нормалью к плоскости контура и магнитной индукцией  ;
;  – проекция вектора
– проекция вектора  на нормаль к плоскости контура;
на нормаль к плоскости контура;
б) в случае неоднородного поля и произвольной поверхности
 (22Ф)
(22Ф)
где интегрирование ведется по всей поверхности.
18. Работа по перемещению контура с током в магнитном поле
 (23Ф)
(23Ф)
где  – приращение магнитного потока через поверхность, ограниченную контуром.
– приращение магнитного потока через поверхность, ограниченную контуром.
19. Э. д. с. индукции (закон электромагнитной индукции)

где знак минус обусловлен правилом Ленца: индукционный ток нап-
равлен таким образом, чтобы своим магнитным полем препятствовать изменению магнитного поля, которое вызвало его.
20. Э. д. с. индукции в проводнике длиной l, движущемся со скоростью  в магнитном поле индукции В,
в магнитном поле индукции В,
|
|
|
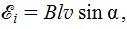 (25Ф)
(25Ф)
где В и v – модули магнитной индукции и скорости проводника; α – угол между скоростью v и магнитной индукцией В.
21. Индуктивность контура

22. Э. д. с. самоиндукции

23. Индуктивность соленоида:
 )
)
где n – число витков, приходящееся на единицу длины соленоида; V – объем соленоида.
Волновая оптика
24. Скорость света в среде
v = c / n, (29Ф)
где с – скорость света в вакууме; n – абсолютный показатель преломления среды (находятся из таблицы).
25. Оптическая разность хода интерферирующих монохроматических волн
 , (30Ф)
, (30Ф)
где n 1, n 2 – абсолютные показатели преломления сред, в которых распространяются когерентные волны; r 1, r 2 – расстояния от когерентных источников до точки, где наблюдается интерференция.
26. Разность фаз световых волн
 , (31Ф)
, (31Ф)
где λ – длина световой волны, распространяющейся в вакууме.
27. Условие интерференционных максимумов (максимальной интенсивности света)
 , m = 0, ±1, ±2, …, (32Ф)
, m = 0, ±1, ±2, …, (32Ф)
где m – порядок интерференции.
28. Условие интерференционных минимумов (минимальной интенсивности света)
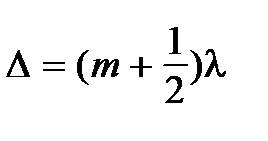 . (33Ф)
. (33Ф)
29. Ширина интерференционной полосы (расстояние между соседними максимумами или минимумами)
 , (34Ф)
, (34Ф)
где L – расстояние от линейных источников света (щелей) до экрана, где наблюдается интерференция; d – расстояние между щелями.
30. Оптическая разность хода монохроматических когерентных волн при отражении от тонкой пленки, находящейся в воздухе,
 , (35Ф)
, (35Ф)
или
 , (36Ф)
, (36Ф)
где n – показатель преломления пленки; d – толщина пленки; β – угол преломления света в пленке; α – угол падения.
31. Радиус светлых колец Ньютона в отраженном свете (или темных – в проходящем)
 (37Ф)
(37Ф)
где m – порядок интерференции или номер кольца; R – радиус кривизны плосковыпуклой линзы
32. Радиус темных колец Ньютона в отраженном свете (или светлых – в проходящем)
 . (38Ф)
. (38Ф)
33. Условие дифракционных максимумов при дифракции света на дифракционной решетке (формула дифракционной решетки)
d sinφ = m λ, m = ±1, ±2, ±3, …,(39Ф)
где d – период или постоянная решетки; φ – угол дифракции (угол между нормалью к поверхности решетки и направлением дифрагированных лучей); m – порядок дифракционного максимума или спектра. При освещении решетки белым светом число m называется порядком дифракционного спектра.
34. Закон Малюса
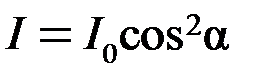 , (40Ф)
, (40Ф)
где I 0, I – интенсивность плоско поляризованного света, вышедшего соответственно из поляризатора и анализатора; α – угол между плоскостями пропускания поляризатора и анализатора.
35. Закон преломления света
 , (41Ф)
, (41Ф)
где α – угол падения; β – угол преломления; n 1, n 2 – абсолютные показатели преломления первой и второй сред; n 21 – относительный показатель преломления второй среды относительно первой.
36. Закон Брюстера
 , (42Ф)
, (42Ф)
где αБ – угол Брюстера (угол падения, при котором отраженная световая волна является полностью поляризованной, и колебания све-
тового вектора Е происходят в плоскости, перпендикулярной плоскости падения света).
37. Угол поворота плоскости поляризации монохроматического света при прохождении через оптически активное твердое вещество:
j = α l, (43Ф)
где α – постоянная вращения, зависящая от природы вещества и длины волны; l – длина пути, пройденного светом в оптически активном веществе (толщина пластины, через которую проходит свет).
Примеры решения задач
Пример 1. К источнику тока с э. д. с.  и и внутренним сопротивлением
и и внутренним сопротивлением  подключен нагревательный прибор, который потребляет тепловую мощность
подключен нагревательный прибор, который потребляет тепловую мощность  . Найти силу тока в цепи и к. п. д. η источника тока.
. Найти силу тока в цепи и к. п. д. η источника тока.
Решение
   , ,
   , ,
   . .
|
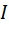  ? ?  =? =?
|
Силу тока выразим по закону Ома для замкнутой цепи, который получается из закона для неоднородного участка цепи (5Ф). Для нашей задачи разность потенциалов φ1 – φ2 = 0 и сопротивление R 12 = R + r.

Сопротивление внешней цепи  найдем из первой формулы мощности (11Ф)
найдем из первой формулы мощности (11Ф)

Подставляя (2) в (1), получим квадратное уравнение относительно тока 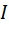 :
:

Решая это квадратное уравнение, найдем силу тока в цепи:
 ;
; 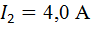 . (3)
. (3)
Два значения тока соответствуют двум сопротивлениям внешней цепи (см. (2))
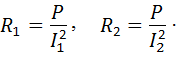
Очевидно, величина  есть полная мощность, выделяемая во всей цепи. Тогда к. п. д. источника тока
есть полная мощность, выделяемая во всей цепи. Тогда к. п. д. источника тока

Учитывая (3) и условие задачи, получим:
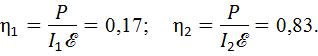
Пример 2. Два последовательно соединенных источника тока имеют одинаковые э. д. с. и разные внутренние сопротивления  и
и  . При каком внешнем сопротивлении
. При каком внешнем сопротивлении  разность потенциалов на полюсах источника с внутренним сопротивлением
разность потенциалов на полюсах источника с внутренним сопротивлением  будет равна нулю?
будет равна нулю?
 , ,
 , ,
 =0. =0.
|
 =? =?
|
Решение

|
| 1 |

|

|
| 2 |

|

|

|
| Рис. 1 |
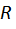
|

|

|
| + |
| 3 |
Последовательное соединение источников тока, замкнутых на внешнее сопротивление  , показано на рис. 1. Используем закон Ома для неоднородного участка цепи (обобщенный закон Ома) (5Ф). Выбранные направления обхода участков цепи (на рис. показаны стрелкой) совпадают с направлением действия сторонних сил и с направлением тока в цепи. Следовательно, э. д. с.
, показано на рис. 1. Используем закон Ома для неоднородного участка цепи (обобщенный закон Ома) (5Ф). Выбранные направления обхода участков цепи (на рис. показаны стрелкой) совпадают с направлением действия сторонних сил и с направлением тока в цепи. Следовательно, э. д. с.  и
и  . Используя эти правила знаков и обозначения на рисунке, запишем закон Ома для участков (1 – 2), (2 – 3) и (3 – 1):
. Используя эти правила знаков и обозначения на рисунке, запишем закон Ома для участков (1 – 2), (2 – 3) и (3 – 1):
 , (1)
, (1)
 , (2)
, (2)
 , (3)
, (3)
где 
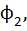

 потенциалы в точках 1, 2, 3 (см. рис. 1). Складывая уравнения (1) – (3), получим:
потенциалы в точках 1, 2, 3 (см. рис. 1). Складывая уравнения (1) – (3), получим:

Учитывая условие задачи  , выразим ток
, выразим ток 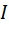 из (1)
из (1)

Из уравнений (4), (5) найдем искомое внешнее сопротивление
 .
.
Для нахождения тока 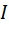 (см. (4)) можно использовать также второй закон Кирхгофа (10Ф). Этот закон выводится из обобщенного закона Ома (в нашей задаче из уравнений (1) – (3)).
(см. (4)) можно использовать также второй закон Кирхгофа (10Ф). Этот закон выводится из обобщенного закона Ома (в нашей задаче из уравнений (1) – (3)).
Пример 3. Источник тока замыкается один раз на резистор сопротивлением  , другой – на резистор сопротивлением R 2 = 6 Ом, в обоих случаях на них выделяется одинаковая мощность. При каком сопротивлении
, другой – на резистор сопротивлением R 2 = 6 Ом, в обоих случаях на них выделяется одинаковая мощность. При каком сопротивлении  мощность будет максимальной?
мощность будет максимальной?
Решение
 = =  , ,
 = =  , ,
 = =  , ,
 = =  . .
|
 =? =?
|
Используем формулу мощности (11Ф)
 (1)
(1)
Сила тока находится из закона Ома для замкнутой цепи

где 
 э. д. с. источника тока;
э. д. с. источника тока; 
 внешнее сопротивление;
внешнее сопротивление; 
 внутренне сопротивление источника. Учитывая (2), имеем из (1):
внутренне сопротивление источника. Учитывая (2), имеем из (1):

Получили зависимость мощности  от внешнего сопротивления
от внешнего сопротивления  . По условию задачи мощности, выделяемые на резисторах сопро-
. По условию задачи мощности, выделяемые на резисторах сопро-
тивлением  и
и  , равны:
, равны:  или, учитывая (3), получим:
или, учитывая (3), получим:

Решая это уравнение относительно внутреннего сопротивления r, получим:

Для нахождения сопротивления  , при котором мощность будет максимальной, необходимо зависимость (3), или функцию
, при котором мощность будет максимальной, необходимо зависимость (3), или функцию 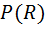 исследовать на экстремум, т. е. производную мощности
исследовать на экстремум, т. е. производную мощности  по сопротивлению
по сопротивлению  приравнять нулю
приравнять нулю
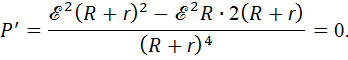
Откуда имеем  , или, учитывая (4), найдем сопротивление, при котором мощность будет максимальной
, или, учитывая (4), найдем сопротивление, при котором мощность будет максимальной
 .
.
Пример 4. От источника тока с э. д. с.  и внутренним сопротивлением
и внутренним сопротивлением  необходимо протянуть к потребителю двухпроводную линию на расстояние
необходимо протянуть к потребителю двухпроводную линию на расстояние  100 м. Определить наименьшее сечение алюминиевого провода, необходимого для этого, если максимальная мощность потребителя
100 м. Определить наименьшее сечение алюминиевого провода, необходимого для этого, если максимальная мощность потребителя  22 кВт и он рассчитан на напряжение
22 кВт и он рассчитан на напряжение  220 В.
220 В.
Решение
 250 В, 250 В,
 0,10 Ом, 0,10 Ом,
 100 м, 100 м,
 , ,
 220 В. 220 В.
|
  ? ?
|
Запишем для нашей задачи закон Ома для замкнутой цепи

Здесь ток 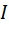 находится из формулы мощности потребителя
находится из формулы мощности потребителя 

Сопротивление проводов (см. (6Ф))

где ρ = 25 нОм.м (при 20оС) – удельное сопротивление алюминия (находится из таблицы);  – искомое минимальное сечение проводов; коэффициент 2 учитывает двухпроводную линию. Сопротивление
– искомое минимальное сечение проводов; коэффициент 2 учитывает двухпроводную линию. Сопротивление  потребителя находится из второй формулы мощности (11Ф)
потребителя находится из второй формулы мощности (11Ф)

Подставляя формулы 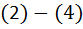 в (1), найдем из полученного уравнения:
в (1), найдем из полученного уравнения:

Найденное сечение является минимальным, т. к. при меньшем сечении проводов увеличивается их сопротивление и уменьшается ток в цепи. Следовательно, мощность не будет максимальной.
Пример 5. Ток I = 5,0 А течет по тонкому замкнутому проводнику (рис. 2). Радиус изогнутой части проводника R = 120 мм, угол 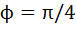 . Найти магнитную индукцию B в точке О.
. Найти магнитную индукцию B в точке О.
Решение
I = 5,0 А,
R = 0,12 м,
 . .
|
| B =? |
| Рис. 2 |
| I |
| d I |
| l |

|

|
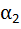
|

|
| φ |
| r |
| B |
| C |
| A |
| O |
| a |
| R |
 ,создаваемой током I, текущим в круговой части l контура и индукции
,создаваемой током I, текущим в круговой части l контура и индукции 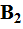 от прямого участка контура AC (рис. 2). По правилу правого винта индукции
от прямого участка контура AC (рис. 2). По правилу правого винта индукции  и
и 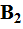 в точке О направлены в одну сторону «от нас», следовательно, искомая индукция B также направлена «от нас» (на рис. показана крестиком Ä). Тогда модуль индукции B равен
в точке О направлены в одну сторону «от нас», следовательно, искомая индукция B также направлена «от нас» (на рис. показана крестиком Ä). Тогда модуль индукции B равен
 (1)
(1)
Величина  находится из закона Био – Савара, записанного для модуля индукции dB, создаваемойэлементом dl контура с током (см. (13Ф) и рис. 2)
находится из закона Био – Савара, записанного для модуля индукции dB, создаваемойэлементом dl контура с током (см. (13Ф) и рис. 2)

Из рис. 2 видно r = R и  (
( ). Интегрируя выражение (2) по длине l кривой части контура, получим:
). Интегрируя выражение (2) по длине l кривой части контура, получим:

Учли, что длина дуги l = 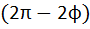 R (см. рис.). Модуль индукции от участка AC контура находится по формуле (выводится из закона Био – Савара (13Ф))
R (см. рис.). Модуль индукции от участка AC контура находится по формуле (выводится из закона Био – Савара (13Ф))

Из рисунка видно: 
 a = R
a = R  – расстояние от прямолинейного проводника AC до точки О. С учетом этого, из (4) имеем:
– расстояние от прямолинейного проводника AC до точки О. С учетом этого, из (4) имеем:
 Учитывая (3) и (5), из (1) найдем модуль искомой индукции:
Учитывая (3) и (5), из (1) найдем модуль искомой индукции:

Пример 6. Определить индукцию магнитного поля B в точке О, если проводник с током I = 5,0 A имеет вид, показанный на рис. 3 Радиус изогнутой части проводника R = 10 см, прямолинейные участки проводника предполагаются очень длинными.
Решение
| I = 5,0 А, R = 0,10 м. |
| В=? |
| O |

|
| 2 |

|
| R |
| I |

|
| 1 |

|
| Рис. 3 |
 , (1)
, (1)
где  – магнитные индукции в точке О,создаваемые токами, текущими соответственно на участках 1, 2 и 3. По правилу правого винтавекторы
– магнитные индукции в точке О,создаваемые токами, текущими соответственно на участках 1, 2 и 3. По правилу правого винтавекторы  направлены перпендикулярно плоскости рисунка «от нас» и векторное равенство (1) можно заменить арифметическим
направлены перпендикулярно плоскости рисунка «от нас» и векторное равенство (1) можно заменить арифметическим
 . (2)
. (2)
Модуль магнитной индукции  находится по формуле индукции в центре кругового тока (см. (14Ф)). У нас магнитное поле создается половиной кругового тока (см. рис.). Поэтому
находится по формуле индукции в центре кругового тока (см. (14Ф)). У нас магнитное поле создается половиной кругового тока (см. рис.). Поэтому
 Для нахождения индукций
Для нахождения индукций 
 воспользуемся формулой
воспользуемся формулой
 В нашей задаче для проводника 2 углы
В нашей задаче для проводника 2 углы  ,
, 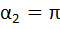 .Для проводника 3 имеем:
.Для проводника 3 имеем:  (см. рис.). Расстояние от точки О до прямолинейных проводников a = R.
(см. рис.). Расстояние от точки О до прямолинейных проводников a = R.
В результате из (4) имеем

Используя (3) и (5), получим из (2) искомую индукцию:
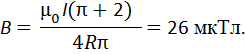
Пример 7. Проводник в виде тонкого полукольца радиусом R = 10 см находится в однородном магнитном поле с индукцией В = 50 мТл. По проводнику течет ток I = 10 А. Найти силу F, действующую на проводник, если плоскость полукольца перпендикулярна линиям магнитной индукции.
Решение
| R = 0,10 м, В = 50.10–3 Тл, I = 10 A. |
| F =? |
На элемент проводника  с током I, находящийся в магнитном поле с индукцией
с током I, находящийся в магнитном поле с индукцией  действует сила Ампера, модуль которой (см. (18Ф))
действует сила Ампера, модуль которой (см. (18Ф))
 . (1)
. (1)
Направление силы d F, действующей на элемент проводника d l, определяется по правилу левой руки (см. рис. 4). По условию задачи магнитная индукция  перпендикулярна плоско
перпендикулярна плоско
|
|
|


