 |
Квантовая оптика. Атомная и ядерная физика
|
|
|
|
Основные формулы
Квантовая оптика
1. Закон Стефана – Больцмана
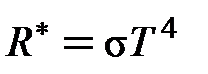, (1Ф)
где R * – энергетическая светимость абсолютно черного тела, т. е. энергия, излучаемая с единичной поверхности тела за единицу времени во всем интервале длин волн; σ – постоянная Стефана – Больцмана; T – термодинамическая температура.
2. Закон смещения Вина
, (2Ф)
где λ m – длина волны, на которую приходится максимум энергетической светимости абсолютно черного тела; b – постоянная Вина.
3. Энергия фотона
, (3Ф)
где h – постоянная Планка; ν – частота света; с – скорость света в вакууме; λ – длина волны фотона.
4. Импульс фотона
p = h /λ. (4Ф)
5. Уравнение Эйнштейна для фотоэффекта
, (5Ф)
где h ν = ε – энергия поглощенного фотона; A – работа выхода электрона из вещества; m – масса электрона; v max – максимальная скорость вылетающего электрона.
6. Красная граница фотоэффекта
или 
, (6Ф)
где ν0, l0 – соответственно минимальная частота и максимальная длина волны света, при которых еще возможен фотоэффект.
7. Формула Комптона
(7Ф)
где ∆l = l ¢ – λ – комптоновское смещение; l – длина волны фотона, сталкивающегося со свободным электроном; l ¢ – длина волны фотона, рассеянного на угол α после его столкновения с электроном; m – масса электрона; с – скорость фотона, равная скорости света.
Атомная физика
8. Электрон в атоме водорода двигается по круговым стационарным орбитам, при этом атом не излучает энергию. Для стационарных орбит выполняется условие или правило квантования (1-й постулат Бора)
mvrn = nh /2π, или mvrn = nħ, n = 1, 2, 3,…, (8Ф)
где m, v – масса и скорость электрона; rn – радиус n – й орбиты;
n – главное квантовое число; h, как и ħ, – постоянная Планка. Числовые значения h и ħ находятся из таблицы.
|
|
|
9. При переходе атома из стационарного состояния с энергией En в стационарное состояние с меньшей энергией Em происходит излучение кванта света (фотона) с энергией
h ν = En – Em, или ħ ω = En – Em, (9Ф)
где ν – частота света; ω = 2πν – круговая (циклическая) частота. Такое же соотношение выполняется, когда атом поглощает фотон и переходит из стационарного состояния с энергией Em в стационарное состояние с большей энергией En, при этом фотон перестает существовать (2-й постулат Бора).
10. Полная энергия электрона в водородоподобном атоме
(10Ф)
где Z – порядковый номер элемента в таблице Менделеева, для водо-рода Z = 1; е – элементарный заряд, равный модулю заряда электрона; ε0 – электрическая постоянная. Численные значения е и ε0находятся из таблицы.
11. Длина волны света λ, изучаемого атомом водорода при переходе электрона с одной орбиты на другую, определяется из формулы Бальмера
(11Ф)
где R – постоянная Ридберга (находится из таблицы); m, n – квантовые числа. Число m определяет номер спектральной серии, число n принимает все целочисленные значения, начиная с m + 1. При m = 1 наблюдается ультрафиолетовая серия (серия Лаймана), при m =2 – видимая серия (серия Бальмера), при m = 3, 4,… наблюдаются серии в инфракрасной области спектра.
12. Длина волны де Бройля
λ = h/р, (12Ф)
где p = mv – импульс частицы, когда скорость v много меньше скорости света c в вакууме(v << c); 
– релятивистский импульс частицы при v ~ c.
13. Выражения длины волны де Бройля через кинетическую энергию частицы E к:
нерелятивистский случай (v << c)
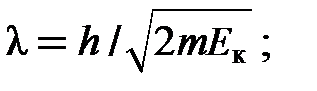(13Ф)
релятивистский случай (v ~ c)
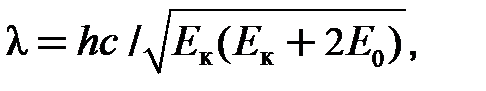(14Ф)
где E 0 = mc 2 – энергия покоя частицы.
14. Соотношение неопределенностей для координаты х и проекции импульса частицы рх
∆ x. ∆ px ³ ћ, (15Ф)
где ∆ x – неопределенность координаты частицы; ∆ px – неопределенность проекции импульса на ось x; ћ = h /2π – постоянная Планка.
|
|
|
15. Соотношение неопределенностей для энергии и времени
∆ E. ∆ t ³ ћ, (16Ф)
где ∆ E неопределенность энергии за промежуток времени ∆ t.
16. Одномерное уравнение Шредингера для стационарных состояний
(17Ф)
где y(x) – волновая функция, описывающая состояние частицы; m – масса частицы; E – полная энергия; U – потенциальная энергия.
17. Вероятность нахождения частицы в интервале от x 1 до x 2
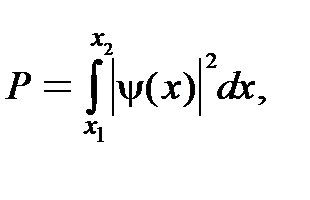(18Ф)
где |y(x)|2 – плотность вероятности нахождения частицы в точке с координатой х.
18. Решение уравнения Шредингера для одномерной, прямоугольной потенциальной ямы с бесконечно высокими стенками:
собственные волновые функции
(19Ф)
собственные значения энергии частицы
n = 1, 2, 3,…, (20Ф)
где n – главное квантовое число; l – ширина потенциальной ямы; m – масса частицы.
Ядерная физика
19. Массовое число ядра (число нуклонов в ядре)
A = Z + N, (21Ф)
где Z – зарядовое число; N – число нейтронов в ядре.
20. Закон радиоактивного распада
N = N 0e – λ t , (22Ф)
где N – число нераспавшихся ядер в момент времени t; N 0 – число ядер в начальный момент времени (t = 0); e = 2,73 – основание натуральных логарифмов; λ – постоянная радиоактивного распада.
21. Число ядер, распавшихся за время t,
∆ N = N 0(1 – e – λ t ). (23Ф)
22. Период полураспада (время, за которое распадается половина первоначального количества ядер)
T = ln2/λ = 0,693/λ. (24Ф)
23. Если промежуток времени t намного меньше периода полураспада Т, то число распавшихся ядер за это время
∆N = λ N 0 t. (25Ф)
24. Среднее время жизни радиоактивного ядра, или промежуток времени, за который первоначальное количество ядер уменьшается в «e» раз
τ = 1/λ. (26Ф)
25. Число атомов, содержащихся в радиоактивном изотопе,
N = mN A / M, (27Ф)
где m – масса образца; N A – постоянная Авогадро; M – молярная масса изотопа (находятся из таблиц).
26. Активность радиоактивного изотопа
а = λ N = λ N 0 e – λ t . (28Ф)
27. Дефект массы ядра
∆m = Zm H + (A – Z) mn – m ат, (29Ф)
где m H – масса атома водорода; m ат – масса атома; mn – масса нейтрона.
28. Энергия связи ядра
E св = ∆m. c 2, (30Ф)
где с – скорость света в вакууме (воздухе).
29. Удельная энергия связи
Е уд = Е св / А = ∆m. c 2/ А. (31Ф)
30. Энергетический выход ядерной реакции (тепловой эффект реакции)
|
|
|
Q = (m 1+ m 2 – m 3 – m 4) с 2, (32Ф)
где – m 1, m 2 – массы исходных частиц или атомов; m 3, m 4 – массы образовавшихся атомов. Если массы атомов выразить в атомных единицах массы (а. е. м.) и воспользоваться соотношением 1 а. е. м.. c 2 = 931,5 МэВ, то энергия реакции будет выражена в МэВ.
Примеры решения задач
Пример. 1. При нагревании абсолютно черного тела длина волны, на которую приходится максимум энергетической светимости, изменилась от λ m 1 = 690 нм до λ m 2 = 500 нм. Во сколько раз увеличилась при этом энергетическая светимость тела R *?
Решение
λ m 1 = 690 нм,
λ m 2 = 500 нм.
 =?
|
, (1)
где температуру Т найдем из закона смещения Вина (2Ф)
. (2)
Выражая отсюда температуру Т и подставляя ее в формулу (1), получим:
. (3)
Энергетическая светимость для двух длин волн λ m 1 и λ m 2
, 
.
Откуда искомое отношение
Энергетическая светимость тела увеличилась в 3,63 раза.
Пример 2. Какова мощность излучения, падающего на зачерненный шарик радиусом r = 2,0 см, если его температура поддерживается на ∆ t = 27 оС выше температуры окружающей среды, которая равна t 1 = 20 ºС? Тепло теряется только на излучение.
Решение
| r = 2,0·10–2м, ∆ t = 27 ºС, t 1 = 20 ºС. ∆Ф =? |
, (1)
где постоянная Стефана – Больцмана σ = 5,67.10 – 8 Вт / (м2.К4), находится из таблицы. Поток Ф, излучаемый телом, равен энергии, излучаемой со всей поверхности тела за единицу времени во всем интервале длин волн. Из этого следует Ф = R * S. Принимая зачерненный шарик за абсолютно черное тело и учитывая (1), запишем поток для температуры Т 1 = t 1+273 = 293 K и T 2 = T 1+∆ T = 320 K, где ∆ Т = ∆ t = 27 К
(2)
где S = 4p r 2 – площадь поверхности шарика. Очевидно, искомый поток ∆Ф = Ф2 – Ф1, или с учетом (2), получим:
Пример 3. Найти частоту света, выбивающего с поверхности металла электроны, которые задерживаются напряжением U з= 3,0 В. Красная граница фотоэффекта n0 = 6,0.1014Гц.
Решение
| U з = 3,0 В, n0= 6,0.1014Гц. n =? |
|
|
|
, (1)
где постоянная Планка h = 6,63.10–34Дж.с; n – искомая частота света. Красная граница фотоэффекта n0 равна такой частоте, при которой максимальная скорость vm = 0. Тогда при n = n0 уравнение (1) примет вид:
. (2)
По условию задачи при задерживающем напряжении U з самые быстрые электроны, имеющие скорость vm, полностью задерживаются электрическим полем, т. е. максимальная кинетическая энергия таких электронов равна работе электрического поля: 
, где е = 1,6.10 – 19Кл – элементарный заряд, равный модулю заряда электрона. Тогда уравнение (1) с учетом (2) запишется:
,
откуда искомая частота света
Гц.
Пример 4. Фотон с энергией ε = 250 кэВ рассеялся под углом α = 120ºна первоначально покоившемся свободном электроне. Найти энергию рассеянного фотона ε'.
Решение
| ε = 0,250 МэВ, α = 120º. ε' =? |
(1)
Рассеяние фотона на электроне описывается формулой Комптона (7Ф), в которой 1 – cosα = 2sin2 (α/2),
. (2)
Подставим в эту формулу длины волн λ' и λ, найденные из (1), и из полученного уравнения выразим искомую энергию ε'
Учитывая числовые данные задачи и энергию покоя электрона mc 2 = 0,51 МэВ, получим числовой ответ:
ε' = 0,144 МэВ.
Пример 5. Атом водорода в основном состоянии поглотил фотон с длиной волны λ = 0,122 мкм. Найти радиус электронной орбиты возбужденного атома.
Решение
| λ = 0,122 мкм. |
| rn =? |
mvrn = nh /2π, n = 1, 2, 3,… (1)
К электрону в атоме водорода применим второй закон Ньютона man = F K, где an = v 2/ rn – нормальное (центростремительное) ускорение; F K= e 2/4πe0 rn 2 – кулоновская сила, действующая на электрон. В результате второй закон Ньютона запишется:
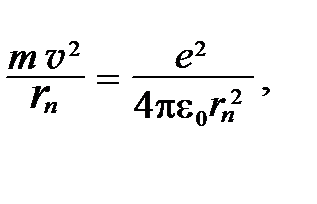(2)
где e – элементарный заряд, равный модулю заряда электрона; ε0 – электрическая постоянная. Из уравнений (1), (2) находим радиус электронной орбиты rn
(3)
где
(4)
постоянная величина (радиус Бора), равная r 0= 5,31.10 – 11м, находится из таблицы. В результате радиус электронной орбиты (3) можно выразить через радиус Бора
rn = r 0 n 2. (5)
Квантовое число n найдем из формулы Бальмера (см. (11Ф))
(6)
где R = 1,10.10 7 м – 1 – постоянная Ридберга, находится из таблицы; m, n – квантовые числа. У нас m = 1, т. к. атом находился в основном состоянии. Тогда из (6) получим n = 2. Подставляя это число в (5), найдем радиус электронной орбиты возбужденного атома:
|
|
|
rn = 2,12.10 – 10 м = 0,212 нм.
Пример 6. Найтициклическую частоту ω вращения электрона на круговой орбите водородоподобного иона гелия Не+ при главном квантовом числе n = 2. С какой линейной скоростью v вращается электрон на заданной орбите?
| Z = 2, n = 2. ω =? v =? |
Воспользуемся вторым законом Ньютона man = F к, где m = 9,11.10 – 31кг – масса электрона; an = ω2 rn – нормальное (центростремительное) ускорение электрона; rn – радиус n – й круговой орбиты электрона; 
– кулоновская сила, действующая на электрон; Z – зарядовое число, для гелия Z = 2; е, ε0 – элементарный заряд (равен модулю заряда электрона) и электрическая постоянная (берутся из таблицы). В результате второй закон Ньютона запишется:
(1)
Используем, далее, первый постулат Бора (8Ф) mvrn = nħ, где v =ω rn – линейная скорость электрона на заданной круговой орбите иона гелия; ħ = 1,05.10 – 34 Дж.с – постоянная Планка. Тогда первый постулат Бора примет вид:
(2)
Решая систему уравнений (1), (2), получим:
(3)
где постоянная величина r 0 = 4πε0 ħ 2/ me 2 = 5,31.10 – 11м называется радиусом Бора (берется из таблицы). В результате (3) запишется:
rn = r 0 n 2/ Z. (4)
Подставляя это выражение в (2), найдем искомую циклическую частоту:
(5)
Используя табличные данные и условие задачи, найдем числовое значение циклической частоты или угловой скорости электрона:
ω = 2,1.1016 с – 1.
Линейная скорость электрона находится из формулы v =ω rn. Учитывая (4) и (5), получим:
Пример 7. С какой минимальной кинетической энергией должен двигаться атом водорода, чтобы при неупругом лобовом (центральном) столкновении с другим, покоящимся атомом водорода, один из них оказался способным испустить фотон? Предполагается, что до столкновения оба атома находились в основном состоянии.
Решение
| H. Е к=? |
mv = 2 mv 1, (1)
где mv – импульс движущегося атома; 2 mv 1 – суммарный импульс двух атомов после центрального неупругого столкновения, в результате которого атомы движутся вместе со скоростью v 1.Заметим, что (1) записано до испускания одним из атомов фотона. Воспользуемся теперь законом сохранения энергии. Энергия системы двух атомов до взаимодействия Е 1 равна кинетической энергии движущегося атома Е к: Е 1 = Е к. После взаимодействия и испускания фотона энергия системы Е 2 складывается из энергии фотона Е ф, и кинетической энергии Е ' кдвух атомов, движущихся вместе со скоростью v 1, Е 2 = Е ф + Е ' к. Применяя закон сохранения энергии Е 1 = Е 2, получим:
Е к = Е ф + Е ' к. (2)
Кинетическая энергия движущегося атома до взаимодействия Е к= mv 2/2. Кинетическая энергия двух атомов после взаимодействия 
Из (1) видно: v 1= v/ 2, тогда Е ' к= mv 2/4. Сравнивая эту энергию с Е к, имеем: Е ' к= Е к/2. Подставляя это в (2), получим:
Е к = 2 Е ф. (3)
Энергия фотона, испускаемого атомом (см. (3Ф)),
Е ф = hc /λ. (4)
Длина волны фотона λ, испускаемого атомом, находится из формулы Бальмера (11Ф):
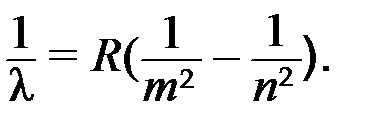(5)
Так как по условию задачи атомы до столкновения находились в основном состоянии, и один из атомов двигался с минимальной кинетической энергией, то в формуле (5) квантовые числа m =1 и n = m + 1 =2. В результате из (5) имеем λ =4/(3 R). Подставим это выражение в (4) и, используя полученный результат, найдем из (3) искомую кинетическую энергию:
Е к = 3 Rhс /2.
Учитывая табличные данные: R =1,10.107м – 1; h =6,63.10 – 34 Дж.с; с =3,00.108 м/с, получим числовой ответ:
Е к = 32,8.10 – 19 Дж = 20,5 эВ.
Пример 8. Найти максимальную длину волны λmax в ультрафиолетовой серии спектра атома водорода, для которой квантовое число m = 1. Какую минимальную скорость v min должны иметь электроны, чтобы при возбуждении атомов водорода ударами электронов появилась линия, соответствующая этой длине волны?
Решение
| m = 1. λmax =? v min=? |
(1)
где R = 1,10.107м – 1 – постоянная Ридберга (находится из таблицы). В нашей задаче дана ультрафиолетовая серия (серия Лаймана), для которой m = 1. Следовательно, n = m + 1 = 2, 3, 4,…. Очевидно, λ = λmax при минимальном значении числа n (см. (1)), т. е. n = 2. Тогда из (1) имеем
λmax= 4/(3 R) = 0,12 мкм. (2)
Для нахождения минимальной скорости электрона v min воспользуемся законом сохранения энергии. Кинетическая энергия электрона равна энергии излучаемого фотона. Скорость v = v min, при λ = λmax
откуда, с учетом (2), найдем искомую скорость
где h – постоянная Планка; c – скорость света; mе – масса электрона. Используя табличные данные: h = 6,63.10 – 34Дж.с; с = 3,00.108м/с; mе = 9,11.10 – 31кг, получим числовой ответ:
v min = 1,9.106м/с = 1,9 Мм/с.
Пример 9. Найти длину волны де Бройля для электрона, имеющего кинетическую энергию: E 1 = 100 эВ; E 2 = 1,0 МэВ.
Решение
| E 1 = 100 эВ = 1,60.10–17Дж, E 2 = 1,0 МэВ = 1,6.10–13Дж. λ 1, λ2 =? |
λ = h/р, (1)
Необходимо сначала установить какова скорость электрона при заданных кинетических энергиях. Для этого нужно сравнить кинетическую энергию электрона с его энергией покоя E 0= mc 2 = 0,51 МэВ. Для энергии E 1= 100 эВ имеем E 1<< E 0,, и электрон является нерелятивистским, т. е. его скорость v намного меньше скорости света с в вакууме. Следовательно, можно пользоваться ньютоновской формулой кинетической энергии
откуда импульс электрона
Подставляя это выражение в (1), найдем длину волны де Бройля для электрона, имеющего кинетическую энергию E 1,
=1,2.10 – 10 м = 120 пм.
Для энергии E 2= 1,0 МэВ имеем E 2>> E 0. Следовательно, электрон является релятивистским и его импульс
В этом случае из (1) найдем длину волны де Бройля для электрона, обладающего энергией E 2,
= 0, 88.10 – 12 м = 0,88 пм.
Пример 10. Кинетическая энергия электрона в невозбужденном атоме водорода E = 13,6 эВ. Используя соотношение неопределенностей, найти минимальную неопределенность координаты электрона в атоме водорода.
Решение
| ∆ x min=? |
| E = 13,6 эВ = 2,18.10–18Дж. Дж. |
∆ рx. ∆ x ≥ ћ, (1)
откуда минимальная неопределенность координаты
∆ x min= ћ /∆ рx. (2)
Физически разумная неопределенность проекции импульса ∆ рx не должна превышать проекции самого импульса рx (∆ рx £ рx). Очевидно также, что проекция рx на фиксированную ось Х лежит в интервале [ – р, р ]. Таким образом, величины ∆ рx и р одного порядка ∆ рx ~ р. Тогда (2) примет вид
∆ x min ~ ћ / р. (3)
Из условия задачи видно, что кинетическая энергия электрона намного меньше его энергии покоя E 0= mc 2 = 0, 51 МэВ. Следовательно, электрон является нерелятивистской частицей, и его импульс 
Подставляя этот импульс в (3), получим ответ:
Пример 11. Частица находится в основном состоянии в одномерной прямоугольной потенциальной яме шириной l с бесконечно высокими стенками. Найти вероятность нахождения частицы в области 0 < x < l /3.
Решение
| 0 < x < l /3, |
| n = 1. |
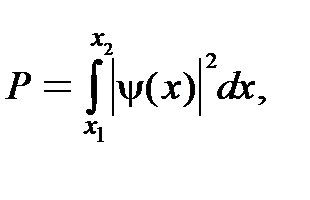| P 1 =? |
(1)
где y(x) = y n (x) – собственная волновая функция частицы. Для одномерной и прямоугольной потенциальной ямы (см. (19Ф))
(2)
где n = 1, 2, 3,…. В нашей задаче n = 1, т. к. частица находится в основном состоянии. Найдем вероятность нахождения частицы в области 0 < x < l /3, используя (1). В нашем случае x 1= 0, x 2 = l /3. Тогда с учетом (2)
(3)
Используя соотношение sin2α = (1 – cos2α)/2, где α = π x / l, вычислим интеграл (3):
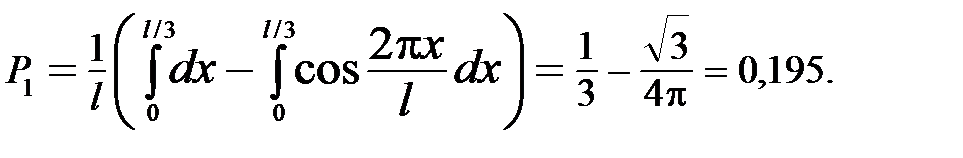
Нашли вероятность нахождения частицы в области 0 < x < l /3.
Пример 12. Сколько ядер распадается в радиоактивном изотопе церия массой m = 1,0 мг в течение времени t 1 = 1,0 c, t 2 = 1,0 год? Период полураспада церия Т = 285 сут.
Решение
| m = 1,0 мг = 1,0.10–6кг, |
| t 1 = 1,0 c, |
| t 2 = 1,0 год, |
| Т = 285 сут. = 2,46.107с. |
| ∆ N 1, ∆ N 2 =? |
∆ N = N 0(1 – е – λ t ). (1)
Здесь N 0 – число ядер в начальный момент времени, которое можно выразить через массу изотопа m, постоянную Авогадро N A = 6,02.1023моль – 1 и молярную массу церия М = 0,14 моль – 1
(2)
Постоянная распада λ в формуле (1) равна (см. (24Ф))
λ = ln2/ Т. (3)
Если промежуток времени t намного меньше периода полураспада Т, то число распавшихся за это время ядер находиться по формуле (см. (25Ф))
∆ N = λ N 0 t. (4)
Таким образом, для времени t = t 1 << T можно пользоваться формулой (4), которая с учетом (2) и (3), примет вид:
(5)
Подставляя сюда числовые данные, получим:
∆ N 1 = 1,2.1012ядер.
Для времени распада t 2 = 1,0 год необходимо пользоваться формулой (1), которая с учетом (2) и (3) запишется:
(6)
Для упрощения числового расчета воспользуемся соотношением eln2 = 2. Тогда
Произведя вычисления, найдем:
∆ N 2 = 2,5.1018ядер.
Пример 13. Найти массу m 1 изотопа урана 238U, имеющего такую же активность, как изотоп стронция 90Sr массой m 2 = 1,00 мг.
Решение
| m 2 = 1,00.10–6кг, а 1 = а 2 = а. m 1 =? |
а = – dN/ dt, (1)
где N – число нераспавшихся ядер в момент времени t. Знак ²минус² означает, что число N уменьшается. Используем закон радиоактивного распада (22Ф)
N = N 0e – λ t , (2)
где N 0 – первоначальное число ядер в момент времени t = 0; λ – постоянная радиоактивного распада, выражается через период полураспада T (см. (24Ф))
λ = ln2/ T. (3)
Продифференцируем уравнение (2) и полученный результат подставим в (1)
а = N 0λe – λ t ,
или с учетом (2) имеем
а = λ N. (4)
Число нераспавшихся ядер N можно выразить через массу изотопа m, постоянную Авогадро N A и молярную массу M
N = mN A/ M. (5)
Подставляя (3) и (5) в (4), получим:
По условию задачи активность урана а 1 равна активности стронция а 2. Тогда, используя (6), имеем:
откуда найдем искомую массу стронция
(7)
Подставляя сюда, взятые из таблиц периоды полураспада и молярные массы урана (T 1, M 1) и стронция (Т 2, М 2), получим ответ:
m 1 = 435 кг.
Пример 14. Найти энергетический выход (тепловой эффект) реакции 10B (n, α) 7Li, протекающей в результате взаимодействия медленных нейтронов с покоящимися ядрами бора. Найти также кинетические энергии продуктов реакции.
Решение
| 10B (n, α) 7Li. |
| Q =?, E Hе =?, E Li =? |
(1)
В соответствии с этой реакцией покоящееся ядро бора 
поглощает медленный нейтрон 
получившееся ядро испускает α-частицу (ядро гелия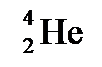 
), и превращается в ядро лития 
Энергетический выход реакции Q находится из формулы (32Ф)
Q = (m 1+ m 2 – m 3 – m 4) c 2. (2)
В нашей задаче m 1= m B – масса атома бора; m 2= mn – масса нейтрона; m 4= m He– масса атома гелия; m 3= m Li– масса лития. Тогда (2) запишется:
Q = (m B+ mn – m Li – m He) c 2. (3)
Если массы атомов и частиц в этом уравнении выразить в атомных единицах массы (а. е. м.) и воспользоваться соотношением c 2 = 931 МэВ/а. е. м., то энергетический выход реакции будет выражен в МэВ. Используя табличные данные, из (3) получим:
Q = 2,80 МэВ.
Для нахождения кинетической энергии продуктов реакции (1) необходимо учесть, что покоящееся ядро бора взаимодействует с медленным нейтроном. Следовательно, кинетической энергией этих частиц можно пренебречь, и в соответствии с законом сохранения энергии, энергетический выход реакции Q будет равен сумме кинетических энергий продуктов реакции
E Li + E He = Q. (4)
Суммарный импульс частиц до реакции равен нулю, т. к. ядро бора покоилось, а нейтрон медленный. Следовательно, суммарный импульс частиц после реакции также равен нулю
рLi + рHe =0.
Отсюда следует, что импульсы частиц направлены в противоположные стороны и равны по модулю
р Li = р He. (5)
Ядра лития и гелия считаем нерелятивистскими (v << c), следовательно, их импульсы равны
где m Li, m He– массы ядер лития и гелия, которые с достаточной для нас точностью равны массам соответствующих атомов. Используя (5), получим:
m Li E Li = m He E He. (6)
Из уравнений (4), (6) найдем искомые энергии
Округляя массы ядер (или атомов) m Li, m He, взятые из таблицы, до целых чисел и, используя найденное значение Q, получим числовые значения кинетических энергий:
E Li = 4 Q /11 = 1,02 МэВ,
E He = 7 Q /11 = 1,78 МэВ.
Пример 15. Найти полезную мощность P пол атомной электростанции, расходующей за сутки уран 235U массой m = 0,10 кг, если к. п. д. электростанции η = 16%. Энергия, выделяемая при распаде одного ядра урана, E 0 = 200 МэВ.
Решение
| m = 0,10 кг, t = 8,64.104с, η = 0,16, E 0 = 3,20.10–11 Дж. P пол =? |
(1)
Мощность P затр находится как энергия, выделяемая за 1 с при распаде N ядер урана, содержащихся в заданной массе,
Р затр= E 0 N / t. (2)
Число ядер N равно числу молей ν = m / M, умноженному на постоянную Авогадро N A (см. (27Ф))
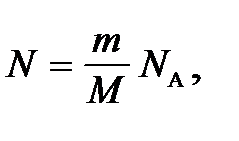(3)
где M – молярная масса урана 235U. С учетом (2), (3) к. п. д. (1) равен
откуда искомая полезная мощность
Таблица вариантов к контрольной работе №4
Таблица содержит варианты для специальностей, учебными планами которых предусмотрено четыре контрольных работы
| Вариант | Номера задач | |||||
|
|
|
