 |
Механический расчет трубопроводов
|
|
|
|
Механический расчет технологических трубопроводов производится на температурные напряжения и на напряжения от изгиба в холодную, когда труба изгибается под собственным весом без нагрева.
В редких случаях производится расчет трубопроводов на внутреннее давление, т.к. трубы изготавливаются на довольно высокие давления, (которых в нефтебазовых трубопроводах практически не бывает).
Толщина стенки технологических трубопроводов определяется по формуле:
(7.1)
где n – коэффициент перегрузки по внутреннему давлению; P – внутреннее рабочее давление в трубопроводе, МПа; R1 – первое расчетное сопротивление материала труб, МПа; DH – наружный диаметр, м.
Первое расчетное сопротивление материала R1 определяется по следующей формуле:
(7.2)
где R1 – первое нормативное сопротивление, соответствующее пределу прочности материала труб, МПа; m – коэффициент условия работы трубопроводов, и т.к. все технологические трубопроводы относятся к высшей категории, то m =0,6; k1 – коэффициент безопасности по материалу труб (для нефтебазовых трубопроводов обычно k1 =1,34 или k1 = 1.4); kH – коэффициент надежности, зависящий от диаметра труб (для труб диаметром dy < 1200 мм k =1).
Обычно толщина стенки, полученная по формуле (7.1), значительно меньше минимальной толщины труб данного диаметра, выпускаемых заводами-изготовителями. Поэтому расчет трубопровода на прочность обычно не производится, диаметр трубопровода определяется из гидравлического расчета, а толщина стенки принимается минимальной для данного диаметра.
Температурные напряжения, возникавшие в стенках трубы, определяются по формуле:
(7.3)
где a – коэффициент линейного расширения; Е – модуль упругости, Н/м2; tэ – максимальная или минимальная рабочая температура стенок трубы в процессе эксплуатации; tф – температура фиксации расчетной схемы трубопровода (температура укладки).
|
|
|
Необходимым условием для возникновения температурных напряжений является жесткая заделка трубопровода. При tэ > tф в стенках возникают сжимающие напряжения, а когда tэ > tф – растягивающие. При подземной укладке трубопровода в нем возникают силы трения грунта о поверхность трубы, которые будут противодействовать растяжению или сжатию трубы от действия температурных напряжений. Сила трения, приходящаяся на единицу длины трубопровода, будет равна:
(7.4)
где Dн – наружный диаметр трубопровода, м; f – коэффициент трения наружной стенки труба о грунт; qгр – удельная нагрузка на трубу от веса грунта, Н/м.
Сила трения противодействует осевой силе, возникающей от действия температурного напряжения, и при определенной длине трубы осевая сила полностью уравновешивается силой трения. Искомая длина определится из условия:
(7.5)
где Fo – площадь сечения металла трубы.
Отсюда
(7.6)
Если фактическая длина трубопровода больше полученной длины, то никаких напряжений в нем возникать не будет.
При рассмотрении напряженного состояния подземного трубопровода необходимо знать его возможное удлинение. Ввиду того, что часть осевой силы подземных трубопроводов компенсируется силой трения, то при одинаковых колебаниях температуры они удлиняются по-разному.
Усилие от сил трения на участке трубопровода dx будет равно T× dx. Напряжение, возникающее в трубе от действия ил трения, будет равно 
. Это напряжение можно выразить через закон Гука:
(7.7)
где de – бесконечно малое относительное удлинение подземного трубопровода на участке dx.
(7.8)
где Dп.з. – абсолютное удлинение трубопровода.
На основании формул (7.7) и (7.8) имеем
(7.9)
Разделяя переменные и интегрируя, найдем абсолютное удлинение подземного трубопровода:
|
|
|
(7.10)
Абсолютное удлинение наземного трубопровода:
(7.11)
Т.е. при одинаковых температурных условиях подземный трубопровод укорачивается или удлиняется в два раза меньше по сравнению с наземным. Отсюда можно сделать вывод, что в подземных трубопроводах надо компенсировать начальные или концевые его участки.
В наземных трубопроводах для снятия температурных напряжений используют различного вида компенсаторы.
Технологические трубопроводы очень часто укладываются на высоких опорах. Такой трубопровод можно представить в виде многопролетной балки. Основной задачей для многопролетной балки является определение допустимой величины пролета. Под действием силы, действующей в пролете, трубопровод прогибается, образуя дугу с радиусом кривизны r, величина которого приближенно равна:
(7.12)
где l – длина пролета; f – стрела прогиба.
От изгиба в стенках трубопровода возникает напряжение, величина которого:
(7.13)
Из курса «Сопротивление материала» известно, что максимальная величина прогиба равна:
(7.14)
где q – удельная расчетная нагрузка от веса металла, изоляции, продукта, снежного покрова и гололеда, Н/м; J – осевой момент инерции трубы, м4.
Подставив выражение (7.14) в (7.13), получим
(7.15)
Максимальная величина пролета определяется из условия:
(7.16)
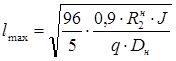(7.17)
|
|
|
